En el segmento de longitud 1 se selecciona aleatoriamente un
Anuncio

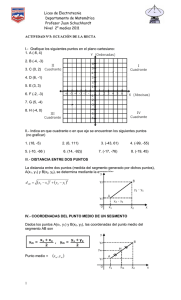
1.- En el segmento AB de longitud 1 se selecciona aleatoriamente un
punto P. En el segmento PB se selecciona aleatoriamente un punto Q.
Calcular la probabilidad de que los segmentos AP , PQ y QB puedan
formar un triángulo.
Y
X
X(=longitud de AP ) ~ U(0,1)
A
P
(Y(=longitud dePQ ) | X=x) ~ U(0,1−x)
X≥0
Y≥0
1−X−Y≥0
⇒
1-X-Y
Q
X+Y≤1
1
fX(x)=1, 0≤x≤1
1
0≤x≤1, 0≤y≤1−x
⇒ f(x,y)=
1
1− x
, 0≤y≤1−x
fY|X=x(y)=
1− x
x+y=1
0
Para formar triángulo:
x+y≥1−x−y
x+1−x−y≥y
y+1−x−y≥x
1
1
2
2
1 −x
0
2
p= ∫ ∫
1
x+y≥1/2
⇒
x+y=1
y≤1/2
x≤1/2
0
1
1
1
1
1
dxdy 12 2 − 2 + x
2 1
= ∫0
dx =
− 1dx = ln2 − ≈0.19
1− x
1− x
2
0 1− x
Simulación:
B
∫
X ~ U(0,1)
(Y|X=x) ~ U(0,1)*(1-x)
1
2.- En el segmento AB de longitud 1 se seleccionan aleatoriamente dos
puntos P y Q. Calcular la probabilidad de que los tres segmentos
resultantes puedan formar un triángulo.
X(=longitud de AP ) ~ U(0,1)
Y(=longitud de AQ ) ~ U(0,1)
A
P
x
A
Q
y-x
P
y
B
1-y
Q
x-y
B
1-x
y-x=1/2
x<y
x<y
x+y−x≥1−y
y≥1/2
x+1−y≥y−x
y−x≤1/2
y−x+1−y≥x
x≤1/2
x>y
x>y
y+x−y≥1−x
x≥1/2
y+1−x≥x−y
x−y≤1/2
x−y+1−x≥y
y≤1/2
x=y
0
x-y=1/2
0
Simulación:
0
X ~ U(0,1)
Y ~ U(0,1)
111 111
+
2
2
2
222 = 1
p=
1
4
3.- En un lanzamiento de tres dados, ¿cuál es la probabilidad de obtener
suma igual a 12?
(1,5,6) £ 3!
(2,4,6) £ 3!
(2,5,5) £ 3
(3,3,6) £ 3
(3,4,5) £ 3!
24
p=
24
6
3
=
1
9
≈ 0.11
4.- Las valoraciones obtenidas en una prueba tienen una distribución
normal de media 5,8 y desviación típica 1,75. Si sólo pasan la prueba
aquellas personas que sobrepasan 6,5 puntos ¿qué porcentaje de
aprobados es de esperar?
X~N(5.8,1.752)
X - 5.8 > 6.5 - 5.8 = P(Z > 0.4 ) = 1−P(Z≤0.4) ≈
1.75
1.75
P(X>6.5)= P
≈ 0.3446
5.- Calcular de forma aproximada la distribución de probabilidad de la
suma de puntos obtenidos al lanzar dos dados.
2
→
(1,1)
3
→
(1,2) (2,1)
4
→
(1,3) (2,2) (3,1)
5
→
(1,4) (2,3) (3,2) (4,1)
6
→
(1,5) (2,4) (3,3) (4,2) (5,1)
7
→
(1,6) (2,5) (3,4) (4,3) (5,2) (6,1)
8
→
(2,6) (3,5) (4,4) (5,3) (6,2)
9
→
(3,6) (4,5) (5,4) (6,3)
10
→
(4,6) (5,5) (6,4)
11
→
(5,6) (6,5)
12
→
(6,6)
℘({2})=℘({12})=
℘({4})=℘({10})=
℘({6})=℘({8})=
1
36
3
36
5
36
℘({3})=℘({11})=
℘({5})=℘({9})=
℘({7})=
6
36
2
36
4
36
6.- Encontrar el máximo y el mínimo de la función y=x3-7x2+14x-8 en el
intervalo (1,4)
y=x3-7x2+14x-8
y’=3x2-14x+14=0
y’’=6x-14
⇒
x=1,45 (máximo) x=3,22 (mínimo)