Las cónicas - Grupo ATP
Anuncio

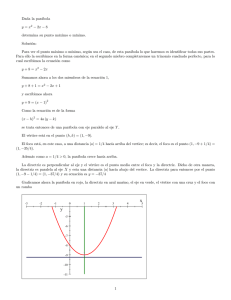
ANDAHUAYLAS PERU Las cónicas Lic. José L. Estrada P. UNAJMA La Parábola Definición Una parábola es el conjunto de todos los puntos del plano que equidistan de un punto fijo F y de una recta fija L del plano. El punto fijo F se llama foco y la recta fija L se llama directriz. Una recta perpendicular a L y que pasa por F se llama eje focal, y el punto del eje que está a la mitad entre la directriz y el foco se llama vértice. Vea la figura 39. Lic. José L. Estrada P. Las cónicas P d2 d1 d3 d5 d4 d6 eje focal Foco (h-p,y) y Vértice p p F = (h+p,k) V = (h,k) Directriz d1 = d2, d3 = d4, d5 = d6 x = h–p Fig. 39 Lic. José L. Estrada P. P = (x,y) Fig. 40 Las cónicas Ecuación en coordenadas cartesianas 1◦ Supongamos que el eje focal es horizontal (directriz vertical), véase la figura 40. Consideremos: V = (h, k) vértice; (h + p, k) foco; p= distancia (positiva) del vértice al foco, ecuación de la directriz: x = h − p; P = (x, y) un punto cualquiera sobre la parábola. Por definición de parábola, igualando distancias d(P, L) = d(P, F ): p p [x − (h − p)]2 + (y − y)2 = [x − (h + p)]2 + (y − k)2 Elevando al cuadrado ambos miembros: x2 − 2x(h − p) + (h − p)2 = x2 − 2x(h + p) + (h + p)2 + (y − k)2 Simplificando se tiene: Ecuación canónica de la parábola (y − k)2 = 4p(x − h) Lic. José L. Estrada P. Las cónicas En particular si el vértice coincide con el origen de coordenadas (0, 0), ver figura 41, entonces la ecuación anterior se reduce a: Ecuación canónica reducida de la parábola y 2 = 4px Directriz x = -p Y Y F=(p,0) b X Fig. 41a Si p > 0 : y 2 = 4px La parábola se abre hacia la derecha Lic. José L. Estrada P. F=(-p,0) b Directriz x=p X Fig. 41b Si p < 0 : y 2 = −4px La parábola se abre hacia la izquierda Las cónicas 2◦ Supongamos que el eje focal es vertical (directriz horizontal). El procedimiento es de la misma forma forma que el caso anterior, igualando las distancias d(P, L) = d(P, F ): p p (x − x)2 + [y − (k − p)]2 = (x − h)2 + [y − (k + p)]2 Simplificando se obtiene: Ecuación canónica de la parábola (x − h)2 = 4p(y − k) Cuando el vértice V = (h, k) coincide con el origen de coordenadas, la ecuación se convierte en: (ver figura 42) Ecuación canónica reducida de la parábola x2 = 4py Lic. José L. Estrada P. Las cónicas 2◦ Supongamos que el eje focal es vertical (directriz horizontal). El procedimiento es de la misma forma forma que el caso anterior, igualando las distancias d(P, L) = d(P, F ): p p (x − x)2 + [y − (k − p)]2 = (x − h)2 + [y − (k + p)]2 Simplificando se obtiene: Ecuación canónica de la parábola (x − h)2 = 4p(y − k) Cuando el vértice V = (h, k) coincide con el origen de coordenadas, la ecuación se convierte en: (ver figura 42) Ecuación canónica reducida de la parábola x2 = 4py Lic. José L. Estrada P. Las cónicas 2◦ Supongamos que el eje focal es vertical (directriz horizontal). El procedimiento es de la misma forma forma que el caso anterior, igualando las distancias d(P, L) = d(P, F ): p p (x − x)2 + [y − (k − p)]2 = (x − h)2 + [y − (k + p)]2 Simplificando se obtiene: Ecuación canónica de la parábola (x − h)2 = 4p(y − k) Cuando el vértice V = (h, k) coincide con el origen de coordenadas, la ecuación se convierte en: (ver figura 42) Ecuación canónica reducida de la parábola x2 = 4py Lic. José L. Estrada P. Las cónicas Representación gráfica - Parábolas paralelas al eje y Y Y y=p Directriz Fig. 42a F=(0,p) b X Fig. 42b b Directriz y = -p F=(0,-p) X Si p > 0 : x2 = 4py La parábola se abre hacia arriba Lic. José L. Estrada P. Si p < 0 : x2 = −4py La parábola se abre hacia abajo Las cónicas Ecuación general Una ecuación cuadrática en dos variables, es de la forma: Ax2 + Bxy + Cy 2 + Dx + Ey + F = 0. Si B = 0 y A = 0 o C = 0 (pero no ambos iguales a cero), entonces esta ecuación representa una parábola. puede ser: Ax2 + Dx + Ey + F = 0 Lic. José L. Estrada P. ó Cy 2 + Dx + Ey + F = 0 Las cónicas Ejemplo 1. Hállese las coordenadas del foco, del vértice y la ecuación de la directriz de la ecuación y 2 − 10x − 8y − 14 = 0. Solución: La ecuación general transfórmese a la forma canónica. Completando cuadrados se tiene: (y 2 − 8y + 16) = 10x + 14 + 16; es decir, (y − 4)2 = 10(x+3). El eje de esta parábola es horizontal y se abre hacia la derecha. Las coordenadas del vértice son V = (h, k) = (−3, 4). Como 4p = 10, entonces p = 52 , y las coordenadas del foco son F = (h + p, k) = (− 21 , 4). La ecuación de la directriz es, x = h − p = − 11 2 . Ejemplo 2. Desde el foco de la parábola y 2 − 4y − 8x + 20 = 0, se ha dirigido un rayo de luz formando un ángulo de 45◦ con el eje focal y al llegar a la parábola se refleja. hallar la ecuación del rayo reflejado: Lic. José L. Estrada P. Las cónicas Solución: Sean L1 y L2 las rectas que siguen los dos rayos. La ecuación y 2 −4y− 8x + 20 = 0 implica que (y − 2)2 = 8(x − 2). Además 4p = 8 implica que p = 2. El vértice se encuentra en (2, 2) y el foco en (4, 2). La pendiente de L1 es m = tan45◦ = 1, y su ecuación será y = x + b. Como (4, 2) está en L1 , entonces 2 = 4 + b, de donde b = −2, luego la ecuación de L1 es y = x − 2. Ahora el punto P0 = (x0 , y0 ) se halla resolviendo el sistema: V=(2,2) Lic. José L. Estrada P. Las cónicas Y 45° F=(4,2) P0 Figura: 43 X L2 y =x−2 (y − 2)2 = 8(x − 2) √ √ En efecto su solución es x0 = 8√− 4 2, y0 = 6 − 4 2. En consecuencia, la ecuación de L2 es y = 6 − 4 2. Véase la figura 43. Lic. José L. Estrada P. Las cónicas Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria Ejercicios 1 Hallar la ecuación de la parábola correspondiente a los siguientes casos: a) b) c) d) 2 Encuentre el vértice, el foco y la directriz de las ecuaciones siguientes: a) b) c) d) 3 Vértice: (0, 0), foco: (0, − 32 ) Vértice: (3, 2), foco: (1, 2) Vértice: (0, 4), directriz: y = 2 Foco: (0, 0), directriz: x = 4 (x − 1)2 = −8(y + 2) 4x − y 2 − 2y − 33 = 0 y 2 + 6y + 8x + 25 = 0 x2 + 4x + 4y − 4 = 0 Hallar la ecuación de la parábola: a) Cuyo eje es vertical y que pasa por los puntos: (0, 3), (3, 4), (4, 11). b) Cuyo eje es horizontal y que pasa por los puntos: (−6, −7), (0, 5), (3/2, −1). Tarea domiciliaria 4 Una manguera situada a una altura de 48 pies de altura sobre el suelo arroja agua a una velocidad de 10 pies/seg. El chorro de agua tiene forma de parábola con vértice en (0, 48) el extremo de la manguera. Observe la figura 44. a) ¿En qué punto del suelo cae el chorro? b) Determine la ecuación de la parábola. (0,48) Figura 44 Tarea domiciliaria 4 Una manguera situada a una altura de 48 pies de altura sobre el suelo arroja agua a una velocidad de 10 pies/seg. El chorro de agua tiene forma de parábola con vértice en (0, 48) el extremo de la manguera. Observe la figura 44. a) ¿En qué punto del suelo cae el chorro? b) Determine la ecuación de la parábola. (0,48) Figura 44 Tarea domiciliaria 4 Una manguera situada a una altura de 48 pies de altura sobre el suelo arroja agua a una velocidad de 10 pies/seg. El chorro de agua tiene forma de parábola con vértice en (0, 48) el extremo de la manguera. Observe la figura 44. a) ¿En qué punto del suelo cae el chorro? b) Determine la ecuación de la parábola. (0,48) Figura 44 Tarea domiciliaria 5 Halle el precio y la cantidad de equilibrio para las ecuaciones de oferta y demanda, donde x representa la cantidad y “y“ representa el precio en los siguientes pares de curvas: a) b) c) d) 6 y + 3x2 − 10 = 0, y = 4 + x2 + 2x y + 2x − 10 = 0, y 2 − 8x − 4 = 0 2x2 + y − 9 = 0, x2 + 5x − y + 1 = 0 2y 2 − x − 3y − 4 = 0, y 2 + y + x − 20 = 0 Una compañia produce cantidades x e y de dos clases diferentes de acero utilizando el mismo proceso de producción. La curva de transformación de producto para la materia prima utilizada está dada por y 2 + x + 4y − 20 = 0. a) ¿Cuáles son las mayores cantidades x e y que se pueden producir? b) ¿Qué cantidades x e y se deben producir para que x = 4y?. Tarea domiciliaria 5 Halle el precio y la cantidad de equilibrio para las ecuaciones de oferta y demanda, donde x representa la cantidad y “y“ representa el precio en los siguientes pares de curvas: a) b) c) d) 6 y + 3x2 − 10 = 0, y = 4 + x2 + 2x y + 2x − 10 = 0, y 2 − 8x − 4 = 0 2x2 + y − 9 = 0, x2 + 5x − y + 1 = 0 2y 2 − x − 3y − 4 = 0, y 2 + y + x − 20 = 0 Una compañia produce cantidades x e y de dos clases diferentes de acero utilizando el mismo proceso de producción. La curva de transformación de producto para la materia prima utilizada está dada por y 2 + x + 4y − 20 = 0. a) ¿Cuáles son las mayores cantidades x e y que se pueden producir? b) ¿Qué cantidades x e y se deben producir para que x = 4y?. Tarea domiciliaria 5 Halle el precio y la cantidad de equilibrio para las ecuaciones de oferta y demanda, donde x representa la cantidad y “y“ representa el precio en los siguientes pares de curvas: a) b) c) d) 6 y + 3x2 − 10 = 0, y = 4 + x2 + 2x y + 2x − 10 = 0, y 2 − 8x − 4 = 0 2x2 + y − 9 = 0, x2 + 5x − y + 1 = 0 2y 2 − x − 3y − 4 = 0, y 2 + y + x − 20 = 0 Una compañia produce cantidades x e y de dos clases diferentes de acero utilizando el mismo proceso de producción. La curva de transformación de producto para la materia prima utilizada está dada por y 2 + x + 4y − 20 = 0. a) ¿Cuáles son las mayores cantidades x e y que se pueden producir? b) ¿Qué cantidades x e y se deben producir para que x = 4y?. Tarea domiciliaria 5 Halle el precio y la cantidad de equilibrio para las ecuaciones de oferta y demanda, donde x representa la cantidad y “y“ representa el precio en los siguientes pares de curvas: a) b) c) d) 6 y + 3x2 − 10 = 0, y = 4 + x2 + 2x y + 2x − 10 = 0, y 2 − 8x − 4 = 0 2x2 + y − 9 = 0, x2 + 5x − y + 1 = 0 2y 2 − x − 3y − 4 = 0, y 2 + y + x − 20 = 0 Una compañia produce cantidades x e y de dos clases diferentes de acero utilizando el mismo proceso de producción. La curva de transformación de producto para la materia prima utilizada está dada por y 2 + x + 4y − 20 = 0. a) ¿Cuáles son las mayores cantidades x e y que se pueden producir? b) ¿Qué cantidades x e y se deben producir para que x = 4y?. Tarea domiciliaria 5 Halle el precio y la cantidad de equilibrio para las ecuaciones de oferta y demanda, donde x representa la cantidad y “y“ representa el precio en los siguientes pares de curvas: a) b) c) d) 6 y + 3x2 − 10 = 0, y = 4 + x2 + 2x y + 2x − 10 = 0, y 2 − 8x − 4 = 0 2x2 + y − 9 = 0, x2 + 5x − y + 1 = 0 2y 2 − x − 3y − 4 = 0, y 2 + y + x − 20 = 0 Una compañia produce cantidades x e y de dos clases diferentes de acero utilizando el mismo proceso de producción. La curva de transformación de producto para la materia prima utilizada está dada por y 2 + x + 4y − 20 = 0. a) ¿Cuáles son las mayores cantidades x e y que se pueden producir? b) ¿Qué cantidades x e y se deben producir para que x = 4y?. Tarea domiciliaria 5 Halle el precio y la cantidad de equilibrio para las ecuaciones de oferta y demanda, donde x representa la cantidad y “y“ representa el precio en los siguientes pares de curvas: a) b) c) d) 6 y + 3x2 − 10 = 0, y = 4 + x2 + 2x y + 2x − 10 = 0, y 2 − 8x − 4 = 0 2x2 + y − 9 = 0, x2 + 5x − y + 1 = 0 2y 2 − x − 3y − 4 = 0, y 2 + y + x − 20 = 0 Una compañia produce cantidades x e y de dos clases diferentes de acero utilizando el mismo proceso de producción. La curva de transformación de producto para la materia prima utilizada está dada por y 2 + x + 4y − 20 = 0. a) ¿Cuáles son las mayores cantidades x e y que se pueden producir? b) ¿Qué cantidades x e y se deben producir para que x = 4y?. Tarea domiciliaria 5 Halle el precio y la cantidad de equilibrio para las ecuaciones de oferta y demanda, donde x representa la cantidad y “y“ representa el precio en los siguientes pares de curvas: a) b) c) d) 6 y + 3x2 − 10 = 0, y = 4 + x2 + 2x y + 2x − 10 = 0, y 2 − 8x − 4 = 0 2x2 + y − 9 = 0, x2 + 5x − y + 1 = 0 2y 2 − x − 3y − 4 = 0, y 2 + y + x − 20 = 0 Una compañia produce cantidades x e y de dos clases diferentes de acero utilizando el mismo proceso de producción. La curva de transformación de producto para la materia prima utilizada está dada por y 2 + x + 4y − 20 = 0. a) ¿Cuáles son las mayores cantidades x e y que se pueden producir? b) ¿Qué cantidades x e y se deben producir para que x = 4y?. Tarea domiciliaria 5 Halle el precio y la cantidad de equilibrio para las ecuaciones de oferta y demanda, donde x representa la cantidad y “y“ representa el precio en los siguientes pares de curvas: a) b) c) d) 6 y + 3x2 − 10 = 0, y = 4 + x2 + 2x y + 2x − 10 = 0, y 2 − 8x − 4 = 0 2x2 + y − 9 = 0, x2 + 5x − y + 1 = 0 2y 2 − x − 3y − 4 = 0, y 2 + y + x − 20 = 0 Una compañia produce cantidades x e y de dos clases diferentes de acero utilizando el mismo proceso de producción. La curva de transformación de producto para la materia prima utilizada está dada por y 2 + x + 4y − 20 = 0. a) ¿Cuáles son las mayores cantidades x e y que se pueden producir? b) ¿Qué cantidades x e y se deben producir para que x = 4y?. Tarea domiciliaria 7 El gerente de producción ha decidido que el departamento de mercado puede vender 126 unidades de un producto diariamente y quiere producir dicha cantidad. Si se asume que todos los factores que no sean el número de empleados y la producción final resultante, permanecen constantes dentro del recorrido de esta producción total, la función de producción se puede expresar mediante la ecuación 2x2 + 4x − y = 0; x es el número de empleados, y las unidades producidas. El gerente afirma que necesitará siete hombres para producir las 126 unidades. a) ¿Está el gerente en lo correcto en su afirmación?. b) Construya un cuadro de las unidades de producto final por hombre empleado, en el intervalo 1 a 7 empleados. Indicar el cambio en el número de empleados, a mediada que agregan uno a uno los empleados, en el mismo intervalo. 8 Hallar la longitud de la cuerda focal de la parábola x2 + 8y = 0 que es paralela a la recta 3x + 4y − 7 = 0. Tarea domiciliaria 7 El gerente de producción ha decidido que el departamento de mercado puede vender 126 unidades de un producto diariamente y quiere producir dicha cantidad. Si se asume que todos los factores que no sean el número de empleados y la producción final resultante, permanecen constantes dentro del recorrido de esta producción total, la función de producción se puede expresar mediante la ecuación 2x2 + 4x − y = 0; x es el número de empleados, y las unidades producidas. El gerente afirma que necesitará siete hombres para producir las 126 unidades. a) ¿Está el gerente en lo correcto en su afirmación?. b) Construya un cuadro de las unidades de producto final por hombre empleado, en el intervalo 1 a 7 empleados. Indicar el cambio en el número de empleados, a mediada que agregan uno a uno los empleados, en el mismo intervalo. 8 Hallar la longitud de la cuerda focal de la parábola x2 + 8y = 0 que es paralela a la recta 3x + 4y − 7 = 0. Tarea domiciliaria 7 El gerente de producción ha decidido que el departamento de mercado puede vender 126 unidades de un producto diariamente y quiere producir dicha cantidad. Si se asume que todos los factores que no sean el número de empleados y la producción final resultante, permanecen constantes dentro del recorrido de esta producción total, la función de producción se puede expresar mediante la ecuación 2x2 + 4x − y = 0; x es el número de empleados, y las unidades producidas. El gerente afirma que necesitará siete hombres para producir las 126 unidades. a) ¿Está el gerente en lo correcto en su afirmación?. b) Construya un cuadro de las unidades de producto final por hombre empleado, en el intervalo 1 a 7 empleados. Indicar el cambio en el número de empleados, a mediada que agregan uno a uno los empleados, en el mismo intervalo. 8 Hallar la longitud de la cuerda focal de la parábola x2 + 8y = 0 que es paralela a la recta 3x + 4y − 7 = 0. Tarea domiciliaria 7 El gerente de producción ha decidido que el departamento de mercado puede vender 126 unidades de un producto diariamente y quiere producir dicha cantidad. Si se asume que todos los factores que no sean el número de empleados y la producción final resultante, permanecen constantes dentro del recorrido de esta producción total, la función de producción se puede expresar mediante la ecuación 2x2 + 4x − y = 0; x es el número de empleados, y las unidades producidas. El gerente afirma que necesitará siete hombres para producir las 126 unidades. a) ¿Está el gerente en lo correcto en su afirmación?. b) Construya un cuadro de las unidades de producto final por hombre empleado, en el intervalo 1 a 7 empleados. Indicar el cambio en el número de empleados, a mediada que agregan uno a uno los empleados, en el mismo intervalo. 8 Hallar la longitud de la cuerda focal de la parábola x2 + 8y = 0 que es paralela a la recta 3x + 4y − 7 = 0. ANDAHUAYLAS PERU UNAJMA Lic. José L. Estrada P.