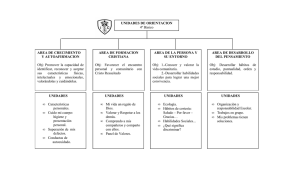
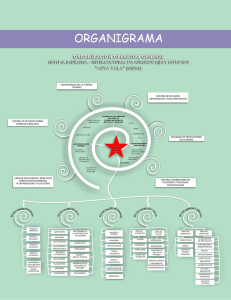
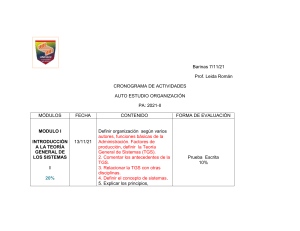
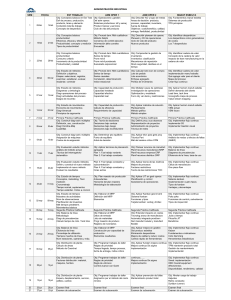
)( )( tytx = )( )( tytxx = )( )( tytx xx = )( )( txtx = x )( )( txtx
Anuncio

337 M de R versión 1 Primera Integral 1/4 Lapso 2008-1 UNIVERSIDAD NACIONAL ABIERTA VICERRECTORADO ACADÉMICO ÁREA : Ingeniería MODELO DE RESPUESTA ASIGNATURA: Simulación de Sistemas MOMENTO: Primera Integral FECHA DE APLICACIÓN: 05-04-2008 CÓDIGO: 337 VERSIÓN: 1 MODULO I. UNIDAD I. OBJ 1 solución No.1. Solución Los estados del sistema están definidos de la siguiente forma: x1 (t ) = y (t ) x2 (t ) = y& (t ) x3 (t ) = &y&(t ) Por ser una ecuación diferencial de tercer orden, solo se necesitan tres estados para identificar completamente su dinámica. Las ecuaciones del sistema son entonces las siguientes: x&1 (t ) = x2 (t ) x&2 (t ) = x3 (t ) x&3 (t ) = −6 x1 (t ) − 11x2 (t ) − 6 x3 (t ) + n(t ) Criterio de corrección Para lograr el objetivo el estudiante debe presentar un resultado equivalente al modelo. Ingeniería de Sistemas 337 M de R versión 1 Primera Integral 2/4 Lapso 2008-1 MODULO I. UNIDAD 2. OBJ 2 solución No.2 Solución Dada la ecuación yn+1 − 3 yn1 = 2, si y2 = 17 se puede escribir como yt+1 – 3yt = 2 en la cual A = 3 y B = 2; como A ≠ 1, aplicando la parte correspondiente de la formula: yt = ⎡1 − A t ⎤ At C + B ⎢ ⎥, si ⎣ 1− A ⎦ y0 + Bt, A ≠1 si A = 1 se tiene: ⎡1− 3t ⎤ t t t yt = 3t C + 2⎢ ⎥ = 3 C − 1− 3 = 3 [C +1] −1 ⎣ 1− 3 ⎦ [ ] donde C es una constante arbitraria. Su valor puede calcularse mediante la condición y2 = 17; sustituyendo t por 2 en la solución anterior y y2 por 17 llegamos a: 17 = y2 = 32 [C + 1] – 1 o sea, 18 = 9[C + 1]; y de aquí se obtiene que C = 1. Remplazando este valor de C, en la solución anterior, se obtiene: yt = 2(3)t – 1 y esta es la solución de la ecuación del problema, según la condición dada. Criterio de corrección Para lograr el objetivo el estudiante debe presentar un resultado equivalente al modelo. Ingeniería de Sistemas 337 M de R versión 1 Primera Integral 3/4 Lapso 2008-1 MODULO II. UNIDAD 3. OBJ 3 No.3 Solución solución Dado el problema de valor inicial: y′(t ) = 5 y (t ) − y (t ), t +1 0 ≤ t ≤ 0,5 con y (0) = 1; Se utiliza el método de Euler para aproximar y (0,5) y n +1 = y 0 + hf ( x 0 , y 0 ) = 0 + 0,1 f ( 0,1 ) = 1, 4 Resumiendo los resultados en la siguiente tabla: 0,1 yn 1,4 0,2 1,89636 0,3 2,49687 0,4 3,20752 0,5 4,03232 t Criterio de corrección Para lograr el objetivo el estudiante debe presentar un resultado equivalente al del modelo. MODULO III. UNIDAD 5. OBJ 5 No.4 Solución solución Empleando las fórmulas del método Predictor-Corrector y ' = 2 x − 3 y + 1, con y (1) = 5, h = 0,1 tendremos: y1, p = y 0 + hf ( x 0 , y 0 ) = 5 + 0 ,1 × (( 2 × 1) − (3 × 5 ) + 1) = 3,8 Ingeniería de Sistemas 337 M de R y1,c = y 0 + versión 1 Primera Integral 4/4 Lapso 2008-1 h ( f ( x0 , y 0 ) + f ( x1 , y1, p ) = 5 + 0,05[((2 × 1) − (3 × 5) + 1) + ((2 × 1,1) − (3 × 3,8) + 1)] = 3,99 2 Así, sucesivamente, tendremos la siguiente tabla de aproximaciones: Valor de t 1,10 1,20 1,30 1,40 1,50 Valor aproximado predictor de y 3,800000 2,980000 2,426000 2,058200 1,820740 Valor aproximado corrector de y 3,990000 3,113000 2,519100 2,123370 1,866359 Criterio de corrección Para lograr el objetivo el estudiante debe presentar un resultado equivalente al del modelo. MODULO III. UNIDAD 6. OBJ 6 solución No.5 Solución El método Lehmer está representado por la formula: Ri+1= (aRi + c) mod m. Si m=12, a=9, c=5 y R0=11, entonces obtenemos los cinco primeros números seudoaleatorios sustituyendo estos valores en la formula: R1 = (9x11+ 5) mod 12 = 8 R2 = (9x8 + 5) mod 12 = 5 R3 = (9x5 + 5) mod 12 = 2 Criterio de corrección Para lograr el objetivo el estudiante debe presentar un resultado equivalente al del modelo. “FIN DE MODELO” Ingeniería de Sistemas