Capítulo 3

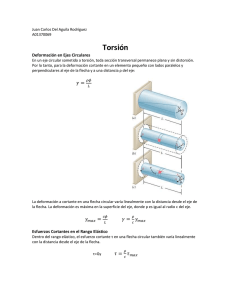
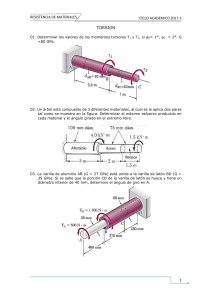
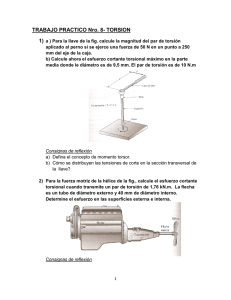
Capítulo 3
Este capítulo se dedicó al estudio de ejes sometidos a torsión. Si se realiza un estudio
preliminar se deduce que la distribución de esfuerzos en la sección transversal de un eje
circular es estáticamente indeterminado. Es por esto que se requiere hacer un análisis de
deformaciones en el eje. Sabiendo que en un eje circular sometido a torsión, la sección
transversal permanece plana y sin distorsión se deduce que:
𝛾=
𝜌ɸ
𝐿
Donde ɸ es el ángulo de giro y p es la distancia del eje.
Puesto que la deformación a cortante varía de manera lineal con la distancia del eje se puede
deducir que:
𝛾𝑚𝑎𝑥 =
𝑐𝜙
𝐿
γ=
𝜌
𝛾𝑚𝑎𝑥
𝑐
También si se consideran los escuerzos cortantes en un eje circular y la ley de Hooke se puede
deducir que:
𝜏=
𝜌
𝜏 𝑚𝑎𝑥
𝑐
Esto significa que dentro del rango elástico, el esfuerzo cortante en una flecha también varía
linealmente con la distancia desde el eje de la flecha. Con esto se dedujo que:
𝜏𝑚𝑎𝑥 =
𝑇𝑐
𝐽
𝜏=
𝑇𝜌
𝐽
Donde c es el radio de la sección transversal y J su momento centroidal polar de inercia.
1
𝐽 = 𝜋𝑐 4 𝑝𝑎𝑟𝑎 𝑢𝑛 𝑒𝑗𝑒 𝑠ó𝑙𝑖𝑑𝑜
2
1
𝐽 = 𝜋(𝑐24 − 𝑐14 )𝑝𝑎𝑟𝑎 𝑢𝑛 𝑒𝑗𝑒 ℎ𝑢𝑒𝑐𝑜
2
Posteriormente se encontró que dentro del rango elástico el ángulo de giro ɸ de un eje es
proporcional a la torsión T, resultando en la fórmula:
𝜙=



𝑇𝐿
𝐽𝐺
J= Momento polar de inercia
L=Longitud del eje
G= Módulo de rigidez del material
Si el eje se somete a torsión en lugares distintos al eje o a distintos ángulos, el ángulo de giro
se representa como la suma algebraica de los ángulos de giro. También se observó que cuando
ambos extremos de un eje son sometidos giran, el ángulo de giro es igual a la diferencia entre
estos.
Para poder diseñar los ejes de transmisión se debe de considerar la potencia mediante la
fórmula:
𝑃 = 2𝜋𝑓𝑇
Para poder analizar las concentraciones de esfuerzos en los ejes circulares se vie que la
concentración de esfuerzos resultante de un cambio repentino en el diámetro del eje puede
reducirse si se utiliza un filete, y para calcular el esfuerzo cortante en el filete se utiliza:
𝜏𝑚𝑎𝑥 = 𝐾
𝑇𝑐
𝐽
Para analizar las deformaciones plásticas y esfuerzos residuales en ejes circulares se debe
recordar que las distribuciones de las deformaciones en estos casos siempre es lineal. Si se
conoce el diagrama esfuerzo-deformación a cortante será posible graficar el este contra la
distancia sumando las contribuciones de estas. Esto se puede expresar como:
𝑐
𝑇 = ∫ 𝑝𝜏(2𝜋𝜌𝑑𝜌) = 2𝜋 ∫ 𝑝2 𝜏𝑑𝑝
0
0
Otro valor que se tiene que considerar es el valor de torsión que causaría la falla del eje
denominado TU el cual puede ser calculado igualándolo con 𝜏max y suponiendo una
distribución lineal de esfuerzos. A este se le conoce como módulo de ruptura y se calcula
mediante:
𝑅𝑡 = 𝑇𝑢𝑐/𝐽
De la misma manera para calcular el valor máximo del par de torsión se calcula mediante:
1
𝑇𝑦 = 𝜋𝑐 3 𝜏𝑦
2
Al aumentar este par de torsión se llega a desarrollar una región plástica en el eje alrededor de
un núcleo elástico de radio py el cual se calcula:
4
1 𝑝𝑦 3
𝑇 = 𝑇𝑦(1 −
)
3
4 𝑐3
Para elementos no circulares, las secciones circulares que puedan tener estos permanecen sin
distorsión. Pero para las secciones no circulares ninguna de las fórmulas anteriores es
aplicable. Para las barras rectas con sección transversal rectangular uniforme, el esfuerzo
cortante máximo ocurre a lo largo de la línea central de la cara más ancha de la barra. Para
ejes huecos no circulares de pared delgada, el esfuerzo cortante es paralelo a la superficie de
la pared