[OOWtE ARC I

I
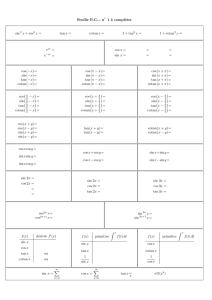
sin 2 x + cos 2 x
::=
sinxsiny
:::: H cos (x - y) - cos (x + y)
cos 2x
=
cos 2 x - sin 2 x
cos x cos y
= H cos ( x + y) +' cos (x - y)
=
2 cos 2 x - 1
sinxcosy
= Hsin(x+y)+sin(x-y)
= 1 - 2 sin 2X
cosxsiny
::=
=
±
Vl-
cos 2 x
=
1 - sin 2x
cos x
=
±-Vl
tan x =
sin x
cot x
cos x '
cos 2 x
sin 2 x
1
sec x
sin x '
=
::=
cos x
sin x
IHALFARCI
1
cos x
1
tan x tn.:
=
+ cot 2 x
!Sin x
=
lSin x
::=
1
::=
csc 2 x
:::
sec 2 x
{
+ 1
I ADDITIoN I·
~
cox
X
==
::=
1 -
=
2 cos(x;
cos 2x
2
cos x + cos
± V l - ~os 2x
sinx+siny = 2 sin(x;Y)cos(x;2Y)
sin x - sin y
COS 2 X
![sin(x+y)-sin(x-y)
2 tan x
== 1 - tan 2x
tan 2x
2
sin 2 x + cos 2 x
I
2 sin x cos x
sin x
=
, PRODUCT
::=
-cos 2x
cot x
I
sin 2x
=1
=
ARC
1
sin 2 x
csc x
[OOWtE
FUNDAMENTAL)
Y=
Y} sin(x 2y)
2 cos(x; y) cos(x;2
cos x - cos y = -2 sin
(~) sin (Y)
1 + cos2x
2
± V l + cos 2x
tan x
sin 2x
= 1 + cos 2x
tan x
_ 1 - cos 2x
sin 2x
REDUCTION OF AcosO + BsinO
For the diagram below, a
(A,B)
= VA2
tan( x ± y) =
+ sin
tan x ±tan y
1 tan x tan y
+
x sin y
+ B
A
=
a cos 4>
B
=
asinql
sin (x ± y) = sin x cos y ± cos x sin y
cos(x± y) = cos x cos y
Y)
For all values of a, Acose + Bsina· = a cos(a - 4»