Document

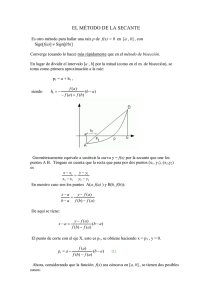
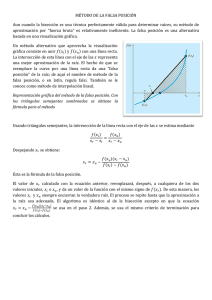
Para resolver:
f(X) = ax2 + bx + c = 0
Se utiliza la formula cuadratica:
 b  b  4ac
x
2a
2
El objeto del calculo de las raíces de una ecuación es
determinar los valores de X para los cuales se cumple
f(X) = 0
Para una función polinómica se cumple que tiene tantas
raíces como el grado del Polinomio:
Método
Grafico
F(x)=0
Métodos
Cerrados
Bisección
Falsa
Posición
Si en un intervalo a, b cerrado se cumple
que f (a) f (b)  0 entonces se tiene que:
Exista un numero
impar de raíces
a
b
a, b cerrado se cumple
Si en un intervalo
que f (a) f (b)  0 entonces se tiene que:
Exista un
numero impar
de raíces
a
b
Si en un intervalo [a,b] cerrado se cumple que
Entonces se tiene que:
f (a) f (b)  0
No existan raíces o haya un numero par de raíces
a
b
Ejemplo: utilizar graficas por computadora para
localizar las raíces de F(x)=x3+x2-3x+5
1500
1000
500
0
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1
-500
-1000
0
1
2
3
4
5
6
7
8
9
10
Ejercicio: utilice el método gráfico para determinar el
coeficiente de arrastre c necesario para que un
paracaidista de masa m=68.1 kg tenga una velocidad de
40 m/s despues de una caida libre de t=10 s.


9.8(68.1)
f (c ) 
1  e ( c / 68.1)10  40
c
o
667.38
f (c ) 
1  e 0.146843c  40
c


1. Buscar un intervalo (xi, xs) de tal forma que la
función cambie de signo:
f ( xi ) . f ( xs )  0
Si se cumple existe al menos
una raíz real entre xi y xs
f(x)
Intervalo en el que se
encuentra la raíz.
f(xi)
f(xs)
xi
xs
2. Se debe hallar el punto medio del
intervalo, tomando el punto de bisección xr como
aproximación de la raíz buscada.
xr
xi
xs
f(xs)
xr

xi  xs 

2
3. Se analiza de manera independiente cada uno de los
intervalos. Se elige entre (xi , xr) y (xr , xs), un intervalo
en el que la función cambie de signo.
Si _ f ( xi ). f ( xr )  0   xs  xr
entonces
Si _ f ( xr ). f ( xs )  0   xi  xr
entonces
Si _ f ( xr ). f ( xs )  0   la _ raiz _ es _ xr
entonces
Error aproximado
Eap 
xractual  xranterior
actual
r
x
100%
Ejemplo: utilice el método de bisección para determinar
el coeficiente de arrastre c necesario para que un
paracaidista de masa m=68.1 kg tenga una velocidad de
40 m/s después de una caída libre de t=10 s.
 F(x)=e-x – ln x, con un E < 1% en el intervalo [1,1.5]
1. Debemos verificar que f (1) y f (1.5) tengan signos
opuestos.
F(1)= e(-1) – ln(1) = 0.3678 f(1) > 0
F(1.5)= e(-1.5) – ln (1.5) = - 0.18233 f(1)< 0
2. Ahora hallamos
Xr = (1+1.5)/2 =1.25
Evaluando Xr = 1.25
f(1.25)= 0.0636 > 0
Repetimos el proceso con el nuevo intervalo [1.25,1.5].
Calculamos el punto medio (que es nuestra segunda
aproximación a la raíz)
Xr = (1.25+1.5)/2 = 1.375
Aquí podemos calcular el primer error aproximado pues ya
contamos con la aproximación actual y la aproximación
anterior:
Eap 
xractual  xranterior
actual
r
x
100%  9.09%
Ahora evaluamos f(1.375)= - 0.06561 < 0
Así, vemos que la raíz se encuentra en el intervalo
[1.25,1.375].
Entonces calculamos el punto medio
Xr = (1.25+1.375)/2=1.3125
Y calculamos el nuevo error aproximado:
Eap 
xractual  xranterior
xractual
100%  4.76%
Se obtuvieron los siguientes datos:
Aprox. a la raíz
1.25
1.375
1.3125
1.28125
1.296875
1.3046875
Error aprox
9.09%
4.76%
2.43%
1.20%
0.59%
Determine las raices reales de f(x)= 5x3 – 5x2 + 6x – 2
Calcule la raiz cuadrada positiva de 18 con E = 0.5% .
Emplee como valores iniciales Xi =4 y Xs = 5.
Una técnica alternativa del método
de bisección, consiste en unir f(xi)
y f(xs) con la línea recta.
La intersección de esta línea con el
eje de las x representa una mejor
aproximación de la raíz. El hecho
de que se reemplacé la curva por
una línea recta da una falsa
posición de la raíz; de aquí el
nombre de método de la falsa
posición, o en latín regula falsa.
También se la conoce como método
de interpolación lineal.
s
s
f ( xi )
f ( xs )

xr  xi xr  xs
f ( xs )( xi  xs )
xr  xs 
f ( xi )  f ( xs )
 CHAPRA, Steven C. y CANALE, Raymond P.: Métodos Numéricos
para Ingenieros. McGraw Hill 2002.
http://lc.fie.umich.mx/~calderon/programacion/notas/Bisecciones.ht
ml
http://www.youtube.com/watch?v=5e1GUYfnc9I
 https://www.ucursos.cl/ingenieria/2008/1/MA33A/1/material_alumnos/objeto/1458
7