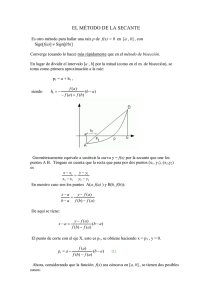
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS ANÁLISIS NUMÉRICO Lic. Gladys G. Melgarejo Estremadoyro SISTEMA NUMÉRICO SISTEMA NUMERICO 1.1 ) Conversión de números enteros del sistema decimal a un sistema de base b y viceversa E1) Convierta 35810 al sistema octal. 358 ∟8 ❻ 44∟8 ❹❺ Entonces 35810 es equivalente a 5468 E2) Convierta 6528 al sistema decimal. 6528 = 6 × 82 + 5 × 81 + 2 × 80 = 42610 Entonces 2768 es equivalente a 19010 E1) Convierta 5468 al sistema binario. Primero aplicaremos Descomposición polinómica. 5468 = 5 × 82 + 4 × 81 + 6 × 80 = 35810 . Luego divisiones sucesivas 358 ∟2 ⓿ 179∟2 ❶ 89∟2 ❶ 44∟2 ⓿ 22……. 2∟2 ⓿❶ Entonces 35810 es equivalente a 1011001102 Por lo tanto 5468 es equivalente al número binario 1011001102 Pero también lo podemos resolver así: 5468 = 5 101 5 ∟2 ❶ 2 ∟2 ⓿ ❶ 4 100 6 110 …….. 1.3 ) Conversión de números fraccionarios del sistema decimal a un sistema de base b E1) Convierta 0510 al sistema octal. 0.5 × 8 4.0 0.4 × 8 3.2 0.2 × 8 1.6 0.6 × 8 4.8 0.8 × 8 6.4 0.4 × 8 3.2 y se repite Entonces 0.510 es equivalente a 0.431468 . Este procedimiento se repite un número suficiente de veces o hasta que la parte decimal sea CERO. 1.4 ) Conversión de un número fraccionario en sistema binario al sistema decimal Generalmente los errores de redondeo se relacionan de manera directa con la forma en que se guardan en la memoria de la computadora. La unidad fundamental de almacenamiento en un computador es la PALABRA, que pueden ser de 8 a 64 bits. A continuación representaciones de los números en la computadora: • Revisaremos como los números de base 10 pueden ser representados en base 2, la aproximación más simple es el método de la MAGNITUD DEL SIGNO, donde el primer bit corresponde al signo, que puede ser (+) cuando es CERO y (-) cuando es UNO 2) NUMEROS REALES (PUNTO FLOTANTE) Al almacenar un número real en su representación binaria se utilizara la notación: 0. 𝑑1 𝑑2 𝑑3 𝑑4 𝑑5 𝑑6 𝑑7 𝑑8 × ′ 𝑑′ 𝑑′ 𝑑′ 𝑑′ 𝑑′ 𝑑′ 𝑑 1 2 3 4 5 6 7 2 Donde 𝑑𝑖 ≈ 0 y 𝑑𝑖 𝑦 𝑑𝑗 con i= 1,….8 ; j=1,2,…7 pueden ser cero o unos. RAICES DE UNA ECUACIÓN INTRODUCCION Nosotros desde hace tiempo aprendimos a utilizar la fórmula: −𝑏 ± 𝑏 2 − 4𝑎𝑐 𝑥= 2𝑎 Para resolver expresiones 𝑝 𝑥 = 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 ó también podemos resolver polinomios lineales 𝑝 𝑥 = 𝑎𝑥 + 𝑏. A estos valores calculados del polinomio ya sea lineal o cuadrático se les llama raíces; es decir 𝑝 𝑥 = 0 es por eso que algunas raíces se les conocen como ceros del polinomio. Aunque la fórmula anterior es útil para resolver ecuaciones polinomiales de segundo grado, hay muchos polinomios que no es posible resolverlos de una manera fácil, en estos casos los métodos numéricos son métodos eficientes para obtener una respuesta. MÉTODO GRÁFICO Este método es útil para obtener una aproximación a la raíz de un polinomio y observar donde cruza ó se intercepta en el eje de las X. Este valor 𝑥 para la cual 𝑝 𝑥 = 0 proporciona una aproximación inicial de la raíz, aunque los métodos gráficos son útiles para obtener estimaciones aproximadas de las raíces, pero pocas precisas. • Para aproximar debemos usar la técnica de PRUEBA ERROR, que es escoger un valor de x y evaluarla si es 𝑝 𝑥 = 0, sino no ocurre así, como en la mayoría de los casos, se hace otra conjetura y se evalúa nuevamente a 𝑝 𝑥 estimación , hasta determinar la mejor hasta encontrar un valor que genere un 𝑝 𝑥 cercano a CERO. Vemos que el gráfico (1) y (3) tienen el mismo signo pero, no hay raíces en la FIG(1). FIG(3) tiene par de ellos entre los valores dados. El grafico (2) nos da el resultado de una raíz que está acotada por valores positivos y negativos de 𝑝 𝑥 Pero no siempre se cumple, pues hay funciones tangenciales ó discontinuas. Así 𝑝 𝑥 = 𝑥 − 2 𝑥 − 2 𝑥 − 4 es un polinomio tangencial pero tiene una raíz múltiple LOCALIZACIÓN DE INTERVALOS DE RAICES DE f(x) =0 Cuando no hay información previa de acerca de los valores aproximados de las raíces; una manera sencilla para hallar intervalos de “x” que contenga una raíz es construir una tabla de valores de x, con separación uniforme. MÉTODOS CERRADOS INTRODUCCIÓN Son aquellos que aprovechan que una función cambia de signo en una vecindad de una raíz. A estas técnicas los llamamos “Métodos Cerrados” o de “Intervalos”, y para ello, son necesarios dos puntos iniciales para encontrar la raíz. Esto implica que dichos valores iniciales deben encerrar a la raíz. Los métodos que vamos a estudiar emplearan diferentes estrategias para reducir el tamaño del intervalo y converger a la respuesta correcta. Entre ellos tenemos: a) Método de Bisección b) Método de Regula Falsi MÉTODO DE BISECCIÓN INTRODUCCION Al graficar la función podemos observaremos que la función cambia de signo en ambos lados de la raíz. Sea 𝒇 𝒙 una función continua y definida en el intervalo, con 𝒇 𝒂 y 𝒇 𝒃 de signos distintos, existe un 𝒙∗ , 𝒂 < 𝒙∗ < 𝒃 tal que 𝒇 𝒙∗ = 𝟎. (Existe una solución ó raíz por el Teorema del Valor Medio). Este método pasos para de Bisección aplica los siguientes una raíz significativas exactas. con ciertas cifras 1)Sea para un intervalo generar inicial donde existe la raíz 𝒙∗ , luego la mediante la relación : sucesión 𝒙𝒊 = 𝒂𝒊 +𝒃𝒊 𝟐 2)Determinar • 𝒇 𝒂𝒊 𝒇 𝒙𝒊 = = > 𝟎 ⇒ 𝒂𝒊+𝟏 = 𝒙𝒊 𝒃𝒊+𝟏 = 𝒃𝒊 < 𝟎 ⇒ 𝒂𝒊+𝟏 = 𝒂𝒊 𝒃𝒊+𝟏 = 𝒙𝒊 𝟎 3) Dejar de iterar sí ⇒ 𝒙𝒊 𝒆𝒔 𝒍𝒂 𝒓𝒂𝒊𝒛 Tolerancia ∞ 𝒙𝒊 ⟶ 𝒙∗ 𝒊=𝟎 , 𝒊 = 𝟏, 𝟐, 𝟑, … , EJEMPLO: Encuentre la raíz de la siguiente ecuación en el intervalo 𝟔 ,𝟕 empleando el método de bisección polinomio error para el 𝒇 𝒙 = 𝒙𝟐 𝒍𝒏 𝒙 − 𝟗𝒙 − 𝟏𝟖 e iterar hasta que el estimado sea menor o igual al 0.01. 𝑓 6 = 6 2 ln 6 − 9 6 − 18 = −7.5 𝑓 7 = 7 2 ln 7 − 9 7 − 18 = 14.35 Si 𝒇 𝟔 𝒇 𝟕 < 𝟎 ⟹ ∃ 𝒙∗ 𝒂 , 𝒃 ; 𝒇 𝒙∗ = 𝟎 Ejemplo La tostación de menas sulfuradas produce una gran contaminación del aire por la emisión de enormes cantidades de óxido de azufre (SO2) a la atmósfera, viene dada por la función: 𝒇 𝒙 = 𝒔𝒆𝒏 𝒙 + 𝒄𝒐𝒔 𝟏 + 𝒙𝟐 − 𝟏 en el intervalo Bisección e 𝟐𝝅 𝟑 ,𝝅 , para ello emplee el método de iterar hasta que el menor que 𝟎. 𝟎𝟎𝟖. (6 dígitos ) error estimado sea 2𝜋 2𝜋 2𝜋 𝑓 = 𝑠𝑒𝑛 + cos 1 + 3 3 3 𝑓 𝜋 = 𝑠𝑒𝑛 𝜋 + cos 1 + 𝜋 Entonces: 𝑓 2𝜋 3 2 𝑓 𝜋 < 0 , ∃ 𝑢𝑛𝑎 𝑟𝑎𝑖𝑧 2 − 1 = 0.490221 − 1 = −1.1256337 𝒏 𝒙𝒏 0 2.617994 1 2.879793 0.261799 2 2.748894 0.130900 3 2.683444 0.065450 4 2.716169 0.032725 5 2.732531 0.016362 6 2.740712 0.008181 7 2.744803 0.004091 ⃒𝒙𝒏+𝟏 − 𝒙𝒏 ⃒ EJEMPLO Encuentre la raíz de la siguiente ecuación en el intervalo −1, −2.5 , empleando el método de Bisección para el polinomio 𝒇 𝒙 = 𝟑𝒙𝟐 − 2𝑥 − 10, e iterar hasta que el error estimado sea menor o igual al 5%. Sea 𝒇 𝒙 = 𝟑𝒙𝟐 − 𝟐𝒙 − 𝟏𝟎, 𝒙∗ 𝝐 −𝟏, −𝟐. 𝟓 con un 𝝃𝒔 ≤ 𝟓% 𝒊 𝒙𝒊 𝒙𝒊+𝟏 − 𝒙𝒊 0 -1.750000000 1 -1.375000000 0.375000000 2 -1.562500000 0.187500000 3 -1.468750000 0.093750000 4 -1.51625000 Luego tenemos que la raíz es: 0.046875000 ≤ 𝟎. 𝟎𝟓 ⟹ 𝒙𝟐 = −𝟏. 𝟓𝟔𝟐𝟓𝟎𝟎 Donde ⃒𝒙𝒊+𝟏 − 𝒙𝒊 ⃒ = 𝟎. 𝟎𝟒𝟔𝟖𝟕𝟓𝟎𝟎𝟎 ≤ 𝟎. 𝟎𝟓 EJEMPLO Aplique el método de Bisección para la función 𝑓 𝑥 = 𝑥 3 − 2𝑥 2 𝑠𝑒𝑛 𝑥 en el intervalo 2 , 3 , e iterar hasta que el error aproximado sea menor que 0.008. Sea 𝑓 𝑥 = 𝑥 3 − 2𝑥 2 𝑠𝑒𝑛 𝑥 , 𝑥 ∗ 𝜖 2 , 3 con un 𝐸𝑎𝑝𝑟𝑜𝑥 < 0.008 No se puede continuar pues, no tiene raiz 𝑬𝒂𝒑𝒓𝒐𝒙 = 𝑬𝑹𝑹𝑶𝑹 𝑨𝑷𝑹𝑶𝑿𝑰𝑴𝑨𝑫𝑶 = ⃒ 𝑨𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒄𝒊ó𝒏 𝑨𝒄𝒕𝒖𝒂𝒍 − 𝑨𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒄𝒊ó𝒏 𝑨𝒏𝒕𝒆𝒓𝒊𝒐𝒓 ⃒ 𝑨𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒄𝒊ó𝒏 𝑨𝒄𝒕𝒖𝒂𝒍 EJEMPLO: Aplique el método de Bisección para la función 𝑓 𝑥 = 𝑥 3 − 2𝑥 2 𝑠𝑒𝑛 𝑥 en el intervalo −2 , 3 , e iterar hasta que el error aproximado sea menor que 0.008. Sea 𝑓 𝑥 = 𝑥 3 − 2𝑥 2 𝑠𝑒𝑛 𝑥 𝐸𝑎𝑝𝑟𝑜𝑥 < 0.008 , 𝑥 ∗ 𝜖 −2 , 3 con un MÉTODO DE REGULA FALSI INTRODUCCION Dado que el Método de Bisección es una técnica que permite determinar raíces, su enfoque no es tan eficiente. La Falsa Posición es una alternativa basada en la visualización gráfica, pues la intersección de una línea con el eje de las X, representa una mejor estimación de la raíz, de aquí el nombre de Falsa Posición, en Latín Regula Falsi ó método de Interpolación Lineal CARACTERISTICAS 1) Este método se basa en la interpolación lineal, es análogo al método de bisección, puesto que el tamaño del intervalo que contiene a la raíz se reduce mediante iteración. 2) El Método de Bisección tiene el defecto que al dividir el intervalo en mitades iguales no considera la magnitud de las imágenes de la función 3) Sin embargo en vez de encontrar los puntos medios de los intervalos en forma monótona , utiliza la interpolación lineal ajustada a dos puntos extremos para encontrar una aproximación de la raíz, siendo la función bien aproximada por la interpolación lineal , entonces las raíces tendrán una buena precisión y la iteración convergerá más rápido que usando el método de bisección. Sabemos que la ecuación de la recta es: 𝑦 − 𝑦0 = 𝑚 𝑥 − 𝑥0 𝑦1 − 𝑦0 𝑦 − 𝑦0 = 𝑥 − 𝑥0 𝑥1 − 𝑥0 Entonces: Sea el intervalo cerrado 𝑎 , 𝑏 que contenga a la raíz , la función lineal que pasa por los puntos : 𝑥1 , 𝑓 𝑥1 𝑦 − 𝑓 𝑥1 , 𝑥0 , 𝑓 𝑥0 , se tiene: 𝑓 𝑥1 − 𝑓 𝑥0 = 𝑥1 − 𝑥0 𝑥1 − 𝑥0 Si 𝑦 = 0 ⟹La recta intersecta al eje X en una raíz Entonces −𝑓 𝑥0 𝑥1 − 𝑥0 𝑥1 = + 𝑥0 𝑓 𝑥1 − 𝑓 𝑥0 𝑥1 − 𝑥0 𝑥1 = 𝑥0 − 𝑓 𝑥0 𝑓 𝑥1 − 𝑓 𝑥0 Entonces: 𝑥2 − 𝑥1 𝑥2 = 𝑥1 − 𝑓 𝑥1 𝑓 𝑥2 − 𝑓 𝑥1 𝑥3 − 𝑥2 𝑥3 = 𝑥2 − 𝑓 𝑥2 𝑓 𝑥3 − 𝑓 𝑥2 Despejando, 𝑥1 tenemos: 𝑦 =0 − 𝑓 𝑥0 𝑥1 − 𝑥0 + 𝑥0 = 𝑥1 𝑓 𝑥1 − 𝑓 𝑥0 • ....... • 𝑥𝑛 = 𝑥𝑛−1 − 𝑥𝑛 −𝑥𝑛−1 𝑓 𝑥𝑛 −𝑓 𝑥𝑛−1 𝑓 𝑥𝑛−1 1) La desventaja de este método es que pueden aparecer extremos fijos así, las aproximaciones 𝑥2 , 𝑥3 , 𝑥4 … … . a la raíz converge solamente por un lado. 2) Los extremos fijos no son deseables, pues hacen más lentos la convergencia, especialmente cuando el intervalo inicial es muy grande. ALGORITMO DEL METODO DE REGULA FALSI EJEMPLO Sea𝑓 𝑥 = 𝑠𝑒𝑛 𝑥 − 𝑐𝑜𝑠𝑒𝑐 𝑥 + 1 para 𝑥 ∗ ∈ [0.5 , 0.7], emplee el Método de Regular Falsi estimado e iterar hasta que el error sea menor e igual a 10−4 Sea 𝑓 0.5 = 𝑠𝑒𝑛 0.5 − 𝑐𝑜𝑠𝑒𝑐 0.5 + 1= − 0.606404 𝑓 0.7 = 𝑠𝑒𝑛 0.7 − 𝑐𝑜𝑠𝑒𝑐 0.7 + 1 = 0.091947 Por lo tanto: 𝑓 0.5 𝑓 0.7 < 0 ⇒ ∃𝑥 ∗ ∈ 0.5, 0.7 , donde 𝜉𝑠 < 10−4 = 0.0001 n 𝒙𝒏 0 0.673667 1 0.667875 0.005791 2 0.666599 0.001275 3 0.666600 0.000100 0.0001 4 0.666319 5 0.666257 𝝃𝒔 EJEMPLO: Encuentre la raíz de 𝑓 𝑥 = 𝑥 4 − 8𝑥 3 − 36𝑥 2 + 462𝑥 − 1010, empleando el método de Regula Falsi, en un intervalo 3.0, 4.0 , e iterar hasta que 𝜉𝑠 ≤ 0.0001%. i xi │Xi+1-Xi │ 0 3.932584270 1 3.902857099 0.000297272 2 3.890154073 0.000127030 3 3.884799978 0.000053541 4 3.882556510 0.000022435 5 3.881618770 0.000009377 6 3.881227212 0.000003916 7 3.881063786 0.000001634 8 3.880995588 0.000000682 9 3.880967131 0.000000285 𝜉𝑠 ≤ 0.0001%= 0.00000 i 0 1 2 3 4 5 6 7 8 9 xi 3.932584 3.902857 3.890154 3.884800 3.882557 3.881619 3.881227 3.881064 3.880996 3.880967 │Xi+1-Xi │ 0.000297 0.000127 0.000054 0.000022 0.000009 0.000004 0.000002 0.000001 𝝃𝒔 ≤ 0.0001%= 0.00000100 0.000000 EJEMPLO: Aplique el método de Falsa Posición de 𝑓 𝑥 = 𝑠𝑒𝑛𝑥 − 𝑥 + 1 en un intervalo 1 ; 3 veces. e iterar seis n Xn │Xi+1-Xi │ 0 1.623230826 0.536616512 1 2.159847338 0.071080873 2 2.230928211 0.007408356 3 2.238336567 0.000748018 4 2.239084585 0.000075277 5 2.239159862 0.000008420 6 2.239168282 0.000000000 7 0.000000000 OBSERVACION 𝑬𝒂𝒑𝒓𝒐𝒙 % = 𝑬𝑨 % = 𝑬𝑹𝑹𝑶𝑹 𝑨𝑷𝑹𝑶𝑿𝑰𝑴𝑨𝑫𝑶% = ⃒ 𝑬𝑹 % = 𝑬𝑹𝑹𝑶𝑹 𝑹𝑬𝑳𝑨𝑻𝑰𝑽𝑶 % = 𝑨𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒄𝒊ó𝒏 𝑨𝒄𝒕𝒖𝒂𝒍 − 𝑨𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒄𝒊ó𝒏 𝑨𝒏𝒕𝒆𝒓𝒊𝒐𝒓 ⃒% 𝑨𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒄𝒊ó𝒏 𝑨𝒄𝒕𝒖𝒂𝒍 𝑽𝒂𝒍𝒐𝒓 𝑽𝒆𝒓𝒅𝒂𝒅𝒆𝒓𝒐 − 𝑽𝒂𝒍𝒐𝒓 𝑨𝒑𝒓𝒐𝒙𝒊𝒎𝒂𝒅𝒐 ⃒ ⃒% 𝑽𝒂𝒍𝒐𝒓 𝑽𝒆𝒓𝒅𝒂𝒅𝒆𝒓𝒐 EJEMPLO Sea 𝑓 𝑥 = 𝑥 4 − 3𝑥 2 + 2𝑥 + 1 𝑥 ∗ ∈ −2, −1 Método de Regular Falsi , emplee el e iterar hasta que el error estimado porcentual sea menor a 10−3 Sea 𝑓 −2 = −2 𝑓 −2 = 1 𝑓 −1 = −1 4 − 3 −2 2 + 2 −2 + 1 4 − 3 −1 2 + 2 −1 + 1𝑓 −1 = − 3 Por lo tanto: 𝑓 −2 𝑓 −1 < 0 ⇒ ∃𝑥 ∗ ∈ −2, −1 , donde 𝜉𝑠 % < 10−3 = 0.001 n 𝒙𝒏 0 -1.7500000 1 -1.9244392 0.17444 2 -1.9392410 0.01480 3 -1.9403105 0.00107 4 -1.9403868 0.00008 𝝃𝒔 % EJEMPLO: Sea 𝑓 𝑥 = 𝐶𝑜𝑠𝑥 3 2𝑥 − 3 𝑥 ∗ ∈ 2 , 9 ( 𝑥 𝑒𝑠𝑡á 𝑒𝑛 𝑟𝑎𝑑𝑖𝑎𝑛𝑒𝑠); emplee el Método de Regular Falsi e iterar 6 veces. n 0 𝒙𝒏 7.1356761 1 8.0916005 2 8.8152968 3 8.6733614 4 8.7260958 5 8.7907143 6 8.7883088 EJEMPLO: Sea f x = x 2 sen x − 5 ( x está en radianes ), determine la raíz positiva más pequeña de la función, empleando el método de Falsa posición para x ∗ ϵ 0 ; 5 . Realice el cálculo hasta que ξs < 0,005 n 𝒙𝒏 𝝃𝒔 0 1.271053198 1 1.996112309 0.725059110 2 2.199467317 0.203355008 3 2.233593225 0.034125908 4 2.238406548 0.0046875000 ≤ 0.05 5 2.239064611 0.000658063 6 2.239168296 0.000103685 7 0.000000000 0.000000014