Cuadernillo Conceptos básicos de triángulos
Anuncio
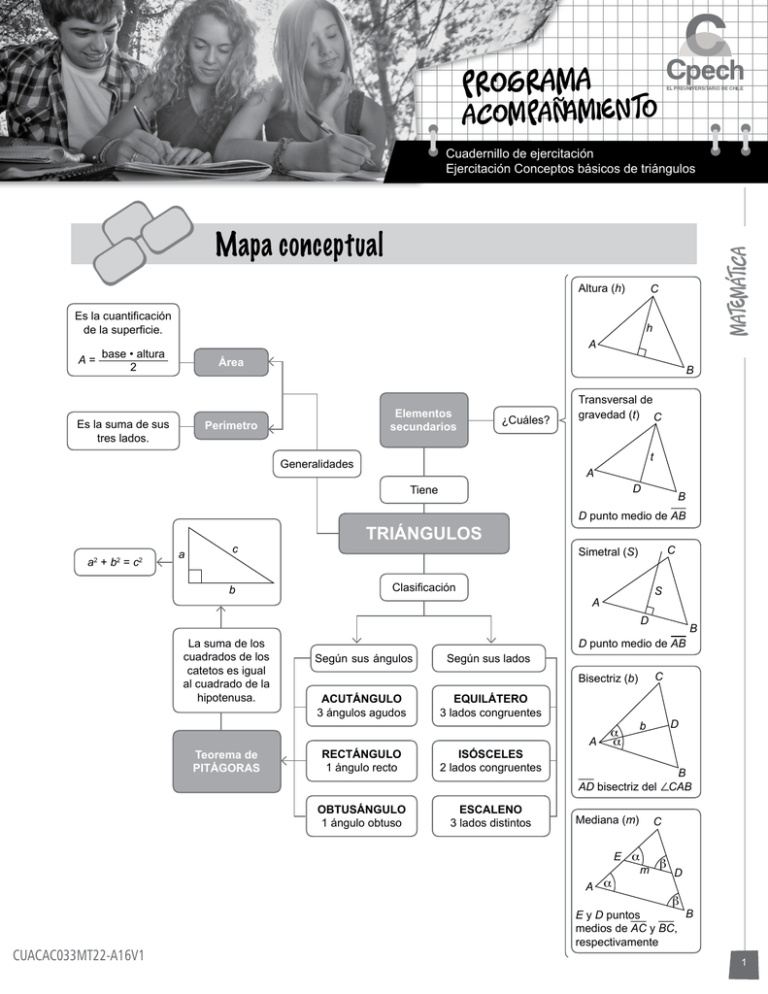
Programa Acompañamiento Cuadernillo de ejercitación Ejercitación Conceptos básicos de triángulos Altura (h) Es la cuantificación de la superficie. A= C h A base • altura 2 Área Es la suma de sus tres lados. B Elementos secundarios Perímetro ¿Cuáles? Transversal de gravedad (t) C t Generalidades A D Tiene a2 + b2 = c2 Matemática Mapa conceptual a c b TRIÁNGULOS B D punto medio de AB C Simetral (S) Clasificación S A D La suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Teorema de PITÁGORAS Según sus ángulos Según sus lados C Bisectriz (b) ACUTÁNGULO 3 ángulos agudos EQUILÁTERO 3 lados congruentes RECTÁNGULO 1 ángulo recto ISÓSCELES 2 lados congruentes OBTUSÁNGULO 1 ángulo obtuso ESCALENO 3 lados distintos B D punto medio de AB A a a D b B AD bisectriz del ∠CAB Mediana (m) E a A a C m b D b CUACAC033MT22-A16V1 B E y D puntos medios de AC y BC, respectivamente 1 MATEMáTICA Ejercicios PSU 1. Según el triángulo de la figura, ¿cuál(es) de las siguientes afirmaciones es (son) verdadera(s)? I) b<a 75º a II) a>b+c α > 75º + 20º III) b 20º A) B) C) D) E) Solo I Solo II Solo III Solo I y II Solo I y III 2. En la figura, BC = α c 8 6 23 , AC = y el perímetro del triángulo ABC es . Entonces, ¿cuál es el 25 25 25 perímetro del triángulo equilátero ADB? 9 A) 25 14 B) 25 27 C) 25 42 D) 25 75 E) 25 2 B C A D CUADERNILLO DE EJERCITACIóN 3. En la figura, AB = MN = 1, AC = KL = RS = 2 y PQ = 4. Si A1 es al área del triángulo 1, A2 es el área del triángulo 2 y A3 es el área del triángulo 3, ¿cuál(es) de las siguientes afirmaciones es (son) FALSA(S)? Triángulo 3 Triángulo 1 R C Triángulo 2 A B K L N M Q S P KM ⊥ NM I) A3 = A1 + A2 II) A1 = A2 III) A3 = 2 A) B) C) D) E) Solo I Solo II Solo III Solo I y II Solo I y III En la figura, AD es transversal de gravedad y su medida es 5 cm. Si el perímetro del triángulo ADC mide 16 cm, entonces el perímetro del triángulo ABC mide C A) 24 cm B) 19 cm D C) 18 cm 6 cm D) 10 cm E) 5 cm 4. A 8 cm B 3 MATEMáTICA 5. En la figura, QS y PT son transversales de gravedad del triángulo escaleno PQR, entonces es FALSO que R A) G es centro de gravedad del triángulo PQR. T S ∠ GQP ≅ ∠ TQG. B) G ST es mediana. C) PG es el doble de GT . D) E)Área ∆ STR = Q P 1 Área ∆ PQR 4 6. En el triángulo ABC de la figura, AD es bisectriz del ángulo BAC, y A, B y E son colineales. La medida del ángulo exterior EBD es A) 50º B) 80º C)100º D)130º E)150º C 30° 100° D E B A 7. En el triángulo ABC de la figura, G es centro de gravedad. Si CG = 30, entonces el triple de GD es A)90 B)45 C)15 D)10 E) 5 C G A 4 D B CUADERNILLO DE EJERCITACIóN 8. En la figura, DE es mediana del triángulo ABC y FG es mediana del triángulo DEC. ¿Qué fracción del área del triangulo ABC es el área sombreada? C 1 A) 16 1 B) 8 3 C) 16 F G E D B A 1 D) 4 1 E) 3 En la figura, D y E son puntos medios de AC y BC, respectivamente. Si el área del triángulo ABC mide 72 cm2, entonces ¿cuánto mide el área achurada? C A) 18 cm2 2 B) 24 cm C) 36 cm2 D E D) 54 cm2 E) Faltan datos para determinarla. 9. A B 10. En la figura, el triángulo ABC es isósceles en B, AD es altura y el ángulo CBA mide 40º, ¿cuánto mide el ángulo DAC? C A)20º D B)40º C)50º D)70º E)90º A B 5 MATEMáTICA 11. En la figura, el triángulo ABC y el triángulo interior en él, son equiláteros cuyos lados miden 6 cm y 3 cm respectivamente. El área achurada mide C 3 A) �3 cm2 2 B)3�3 cm2 C) 27�2 cm2 4 D) 27�3 cm2 4 E) 27�3 cm2 2 A B 12. En la figura, ABC es un triángulo equilátero y DE es mediana. El valor de AE es C A) 4�3 B) 4�2 D C)4 4 E D) 2�3 E) 2�2 A B 13. En la figura, MN es una mediana del triángulo PQT, que es equilátero de lado 10. El perímetro del rectángulo PQRS es A) 10 + 5�3 B) 20 + 5�3 C) 30 D) 20 + 10�3 T S M N R E)40 P 6 Q CUADERNILLO DE EJERCITACIóN 14. En la figura, el triángulo SUT es equilátero de área 25�3 cm2. Se traza un segmento PR, paralelo a SU , de manera que el área del triángulo PRT sea igual al área del cuadrilátero SURP. ¿Cuánto mide PR ? T 5 A) �3 cm 2 B) 5 cm P C)5�2 cm D)5�3 cm E) R S U Faltan datos para determinarlo. 15. En el triángulo CDA de la figura, AB = 2 y BC = 3. El valor de x es A �6 A) �10 B) �5 C)3�2 D)5 E) B ninguno de los valores anteriores. D x C 16. En la figura, hay un gato en la rama de un árbol a una altura h metros del suelo. El dueño del animal debe ayudarlo a bajar utilizando para ello una tabla de tres metros, situada como indica la figura, entonces ¿a cuántos metros de altura se encuentra el gato? A) 1 �2 B) �5 C) 5 D) 2 E) h 5 2 metros 7 MATEMáTICA 17. En la figura aparece una antena de 45 metros de altura que es perpendicular al suelo y que posee cables que la estabilizan, uno de los cuales tiene forma de línea recta. ¿Cuántos metros de longitud posee este cable? A)30 metros B)15�5 metros C)15�10 metros D)60 metros E)45�10 metros 15 metros 18. Una flor perpendicular al suelo está a 40 centímetros del piso y una abeja vuela desde el piso hacia ella en línea recta como muestra la figura. ¿Cuántos centímetros vuela la abeja? A) 2�30 B) 6�15 C)20�5 D)20�10 E) Ninguna de las medidas anteriores. 20 cm 19. En la figura, los puntos A y C pertenecen a la recta L1 y los puntos B y D pertenecen a la recta L2. ¿Cuál de las siguientes afirmaciones es FALSA? L2 A) BD = 3�3 B) OB = 1 B C) OD = 2�3 D) AD = �21 E) AB = �10 • A • 3 O �5 2 4 D• 8 C • L1 CUADERNILLO DE EJERCITACIóN 20. En la figura, el rectángulo ABCD está inscrito en el triángulo PQR, de tal forma que A y D son los puntos medios de sus lados respectivos. Si PQ = 4 cm y PR = RQ = 6 cm, entonces la medida de AB es A) R 2 cm �5 cm B) D) �10 cm D A C)2�2 cm P E)2�5 cm C B Q 21. Respecto de la figura, ¿cuál(es) de las siguientes afirmaciones es (son) verdadera(s)? I) x = 11�2 II) y = 11�10 III) z = 11�5 A) B) C) D) E) Solo I Solo II Solo III Solo II y III I, II y III 33 y 22 x z 11 11 11 11 22. En la figura, AC = 60 cm, BC = 80 cm y AB = 100 cm. Si D es punto medio de AB, entonces ¿cuánto mide CD? A) B) C) D) E) C 50 cm 60 cm 70 cm 80 cm Faltan datos para determinarlo. A D B 9 MATEMáTICA 23. En la figura, el triángulo ABC es rectángulo en C y DE es mediana. Si AC = 5 y CB = 12, el triple de CD es 13 A) 2 C E B)13 C)18 A 39 D) 2 B D E)39 24. En el triángulo ABD de la figura, se puede determinar la medida del ángulo BAD si: (1) (2) DB ⊥ AB El triángulo ABC es equilátero. A) B) C) D) E) (1) por sí sola. (2) por sí sola. Ambas juntas, (1) y (2). Cada una por sí sola, (1) ó (2). Se requiere información adicional. C A 60° D B 25. En la figura, D es punto medio de AB . Se puede determinar la medida de CD si: C (1) AB = 5 cm (2) CB = 4 cm 10 A) B) C) D) E) (1) por sí sola. (2) por sí sola. Ambas juntas, (1) y (2). Cada una por sí sola, (1) ó (2). Se requiere información adicional. A • D B CUADERNILLO DE EJERCITACIóN Tabla de corrección Ítem Alternativa Habilidad 1 Comprensión 2 Aplicación 3 ASE 4 Aplicación 5 Comprensión 6 Aplicación 7 Aplicación 8 Aplicación 9 Aplicación 10 Aplicación 11 Aplicación 12 ASE 13 Aplicación 14 ASE 15 Aplicación 16 Aplicación 17 Aplicación 18 Aplicación 19 Aplicación 20 ASE 21 Comprensión 22 Comprensión 23 Aplicación 24 ASE ASE 25 11 Registro de propiedad intelectual de Cpech. Prohibida su reproducción total o parcial.









