UNIDAD 5. NÚMEROS COMPLEJOS Mapa conceptual LOS
Anuncio
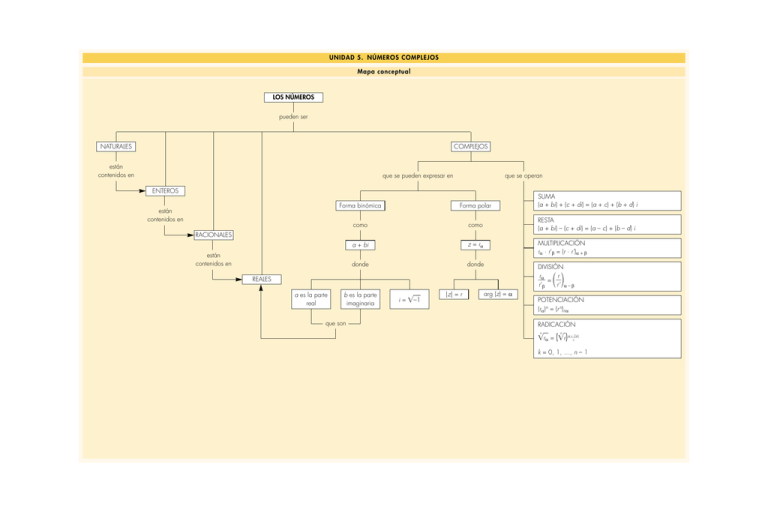
UNIDAD 5. NÚMEROS COMPLEJOS Mapa conceptual LOS NÚMEROS pueden ser NATURALES COMPLEJOS están contenidos en que se operan que se pueden expresar en ENTEROS están contenidos en SUMA (a + bi) + (c + di) = (a + c) + (b + d) i Forma binómica Forma polar como como RESTA (a + bi) – (c + di) = (a – c) + (b – d) i a + bi z = rα MULTIPLICACIÓN rα · r’β = (r · r’)α + β donde donde DIVISIÓN r r α = r’β r’ α – β RACIONALES están contenidos en REALES a es la parte real b es la parte imaginaria que son i= –1 |z| = r arg (z) = α POTENCIACIÓN (rα)n = (r n)nα RADICACIÓN n n α + 2πk rα = (r) n k = 0, 1, …, n – 1











