TEMA 2. CUESTIONES Y PROBLEMAS
Anuncio

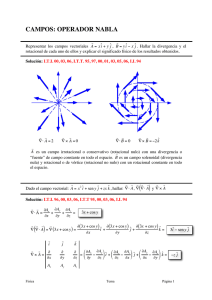
TEMA 2. CUESTIONES Y PROBLEMAS Campos escalares. Gradiente 1. Obtener la ecuación de las superficies isoescalares de la función U y representar dos de ellas. a) U=Kz , K=cte >0. b) U=K/r2 donde r=(x 2+y2+z2)1/2 y K=cte >0. 2. Indicar cómo serían las superficies isotermas (igual valor de la temperatura) en el caso de una fuente de calor: a) Plana, b) Puntual. 3. En la figura se representan 3 superficies equipotenciales del campo escalar U, donde U1>U2>U3. Dibujar el vector gradiente en los puntos A, B y C, resaltando la diferencia entre los módulos. U3 A B C U2 U1 4. a) Dada la función U=xy+z, calcular: la expresión del vector gradiente, grad U, y el gradiente de U para el punto P(1,1,1), grad Up . r r r b) Sí, a partir del punto P, nos desplazamos en la dirección a = 2i + j , ¿cuanto varía la f.e.p. U por unidad de longitud? (Esta variación se conoce como derivada direccional de la función U en la r dirección de a ). r r r r r r Sol.: a) ∇ U = yi + x j + k ∇ U = i + j + k b) 3/√5 p 2 5. Dado el campo escalar U=3x y-y3z2, calcular su gradiente en el punto P(1,-2,-1). r r r Sol.: ∇ U = −12 i − 9 j − 16k Campos vectoriales r 6. Dibujar algunas líneas de campo de la f.v.p. F r r Kr r r r 2 a)F = 2 u r donde ur = y|r |= x 2 + y + z 2 r r 1 r r b)F = Kzk r r c)F = Kxj r d)F = ∆U donde U = Kz Z r r Y X 7. Indicar cuáles de las siguientes afirmaciones son ciertas: -La tangente a la línea de campo en un punto es paralela al vector campo en ese punto. -El gradiente de una función escalar es tangente a las superficies de nivel. -En todos los puntos de una superficie de nivel, la función escalar toma el mismo valor. -Las superficies de nivel de un campo vectorial son normales a la función vectorial en todos los puntos. Circulación. Campos conservativos r r 8. En el plano xy, calcular la circulación de la función F = xi entre los puntos (0,0) y (2,4) a lo largo de la curva y = x 2. Sol.: 2 r r r r 2 2 F = ( 2yz)i +(y + xz)j +(1 2 )k xyz x 9. Calcular la circulación de entre los puntos O(0,0,0) y P(1,1,1). a) a lo largo del segmento que une O y P. b) a lo largo de la curva x=t; y=t2; z=t3. Sol: a) 11/10 b) 4/3 10. Deducir si las siguientes funciones derivan r r de potencial. r r r r r r 2 2 a ) F = 2 xy i + 2 x yj + xyk b ) G = 2 xy 2 i + 2x 2 yj + k Sol.: a) No , b) Si. r r 11. Calcular la f.e.p. U(x,y,z), sabiendo que su gradiente es ∇U = Kr , siendo K una cte >0 y r el vector de posición. En el origen O(0,0,0), U = 0. Dar la solución en función de r. Kr r Idem si ∇ U2 = 2 ur y ∇ U3 = Ke−2 r ur (U 2 ( ∞ ) = 0, U3 ( 0 ) = −1 / 2 ) r 1 k 1 Sol: U = k r 2 , U2 = , U 3 = − e −2 r 2 r 2 2 12. La temperatura en los puntos del plano xy sigue la ley T = 4x 2y + 2y. a) ¿Cuánto vale su gradiente (∇T) en los puntos (0,0) y (1,1)? y b)¿Cuánto vale la circulación del grad T a lo largo de todo el contorno (0,1) cerrado de la superficie de la figura? ¿Por qué? (1,1) r r r Sol.: a) ∇ T(0,0) = 2j ∇ T(1,1) = 8i + 6j b) cero x (1,0) (0,0) Flujo r r 13. Calcular el flujo de la f.v.p. F = Kj , figura. K > 0, de la superficie plana de la z Sol.: Kab/2 b y a 30o x r r 14. Calcular el flujo de F = Kyi , K > 0, a través de la superficie plana de la figura. z 2 Sol.: Kb(a +2ac)/2 c b a y x z r r 15. Calcular el flujo de F = Kj , K > 0, a través de la superficie cerrada de la figura. b a Sol.: cero c r r 16. Calcular el flujo de F = Krur a través de la superficie esférica centrada en el origen de coordenadas y radio R. Sol.:K4πR3 3 y x