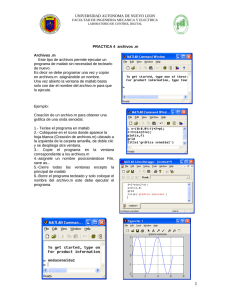
software de aplicación de las transformadas rápidas de fourier (fft)

Autorizada la entrega del proyecto del alumno:
D. Antonio Gordón Romero
Madrid, 24 de junio de 2008
EL DIRECTOR DEL PROYECTO
Fdo.: Dr. D. Francisco Javier Rodríguez Gómez
Vº Bº del Coordinador de Proyectos
Fdo.: D. Eduardo Alcalde Lancharro
Fecha: ……/ ……/ ……
UNIVERSIDAD PONTIFICIA COMILLAS
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA (ICAI)
INGENIERO TÉCNICO EN INFORMÁTICA DE GESTIÓN
PROYECTO FIN DE CARRERA
SOFTWARE DE APLICACIÓN DE LAS
TRANSFORMADAS RÁPIDAS DE
FOURIER (FFT)
AUTOR: ANTONIO GORDÓN ROMERO
MADRID, JUNIO DE 2008
Dedicatoria
A mi familia y amigos, ya que aunque no me habéis podido ayudar en
los números y fórmulas, seréis y sois la luz que me ha guiado durante
todo este año de oscuridad y caídas.
I
Proyecto Fin de Carrera
Agradecimientos
Agradezco la creación y finalización de este proyecto en primer lugar a
mi director de proyecto Francisco Javier Rodríguez Gómez, que confió
en mí durante todo este tiempo, y nunca perdió la paciencia. Sin él este
proyecto no habría llegado a buen puerto.
También quiero agradecer a todas las personas tanto familiares, en
especial a mi padre, como amigos que sin querer han puesto un granito
de arena para conseguir que este proyecto se convierta de un trabajo
pesado a un sueño que significa la culminación de una etapa en mi
vida. No tengo palabras solo decir GRACIAS de todo corazón.
II
Software de Aplicación de la FFT
Resumen
El objetivo de este proyecto será la aplicación del famoso algoritmo de la
Trasformada Discreta de Fourier a distintos problemas en el campo de las matemáticas y
los métodos numéricos. El algoritmo de la FFT descubierto por Jean Baptiste Fourier
(1768-1830), fue en un primer momento estudiado mucho antes por Gauss, quien ideo un
método para descomponer una onda en armónicos simples. Fourier fue más adelante
declarando que cualquier onda se puede descomponer en un sumatorio de ondas armónicas
sinusoidales puras, que darían como resultado la misma señal origen, es más no hacían falta
muchos sumatorios de armónicos con tan solo diez se podría describir la señal origen de
manera casi perfecta. Este gran descubrimiento no fue tenido en cuenta hasta bien entrado
el s. XX donde en 1965 James Cooley y John Tukey de IBM en su estudio sobre
procesamiento de señales digitales redescubrieron y aplicaron esta técnica de Fourier. Esto
fue el inicio de la aplicación del algoritmo de la FFT, ya que a partir de ese momento se
empezó a aplicar a diversos, campos no solo en procesamiento de señales, sino en todas las
ramas de la ciencia.
En la actualidad el algoritmo de la FFT tiene multitud de aplicaciones. En este
proyecto en especial se estudiará la aplicación de dicho algoritmo en el mundo de las
Matemáticas y de Métodos Numéricos.
- Multiplicación de números enteros de gran magnitud.
III
Proyecto Fin de Carrera
- Multiplicación de polinomios de cualquier grado.
- Interpolación Trigonométrica.
- Aproximación rápida de Chebyshev.
Como se observa son problemas que, por un lado, usan operaciones que necesitan
mucho cálculo y tiempo de procesamiento y, por otro lado, hay operaciones de
interpolación de funciones. Todos estos casos, en la actualidad, se resuelven con otras
técnicas, que son comúnmente utilizadas por matemáticos e ingenieros. Lo interesante de
este proyecto es poder tener los mismos resultados, a ser posible con numerosas ventajas
aplicando el algoritmo FFT, tales como más rapidez en el cálculo. Comentar que la
aplicación de Fourier a estos problemas son cada vez más utilizadas y dado que son de
descubrimiento muy reciente, se pretende dar un enfoque pedagógico, como un objetivo de
este proyecto.
Todo ello se va a programar en una herramienta matemática de última generación
muy utilizada en el ámbito académico y de investigación denominada MATLAB. Esta
aplicación posee numerosas bibliotecas con más de trescientas funciones para poder hacer
cualquier cálculo. Una de estas bibliotecas es la FFTW que contiene el algoritmo de la FFT
y ayudará en el cálculo de los diversos módulos que se irán programando. Además,
MATLAB posee una interfaz gráfica llamada GUIDE capaz de programar interfaces
gráficas de usuario de manera sencilla, pudiendo hacer más accesible el programa,
objetivos también del proyecto.
Se diseñará el software sin adecuarse del todo a seguir una metodología típica,
IV
Software de Aplicación de la FFT
como la que se emplea para programar aplicaciones informáticas como es la de Yourdon,
sino se aplicará una más adecuada que realiza una simbiosis entre la metodología antes
citada con la metodología que frecuentemente se usa para proyectos de carácter
matemático, que se resume a continuación.
- Una primera parte será de búsqueda de documentación.
- Estudio de cada problema.
- Obtención final de una lista de requisitos.
- Diseño un pseudocódigo de los problemas, programándolos en MATLAB y
resolviendo con ellos diversos problemas prácticos que servirán de pruebas.
- Seguidamente, cuando se terminen todos los módulos, se empezará con un estudio
de arquitectura y un diseño externo de la interfaz.
- Finalmente se programará la interfaz gráfica de usuario (GUI).
Por último, se trabajará en una guía de instalación donde se explicará de forma
esquematizada pero comprensible cómo instalar y ejecutar el programa, para facilitar el
aprendizaje del usuario.
V
Proyecto Fin de Carrera
Abstract
The objective of this project will be the application of the famous algorithm of the
Discreet Transform of Fourier to different problems in the mathematics field and numerical
methods. The algorithm of the FFT discovered by Jean Baptiste Fourier (1768-1830) had
been formerly studied by Gauss, who devised a method to fragment a wave into simple
harmonic waves. Fourier, however, was more advanced declaring that any wave can be
fragmented into a number of pure sinusoidal harmonic waves, the sum of which will result
in the same original signal, but moreover this number of elements in the sum was not
necessary, only ten harmonic waves would be required to obtain the signal of origin in an
almost perfect way. This great discovery was not considered until the twentieth century. In
1965 James Cooley and John Tukey of IBM while researching digital signal processing rediscovered the FFT and then applied Fourier's technique to their research. This was the
beginning of the application of the algorithm of the FFT, as of that moment it began to
apply to diverse fields not only in signal processing, but in all the branches of science.
Nowadays when Fourier's name is heard, very few people recognize his name, although
with his famous algorithm it is now possible to solve a multitude of cases. In this project
especially we will study the uses of this algorithm in the world of the mathematics and
numerical methods, which is summed up below:
- Multiplication of whole numbers of great magnitude.
- Multiplication of polynomials of any degree.
VI
Software de Aplicación de la FFT
- Trigonometrically Interpolation.
- Fast Approach of Chebyshev.
As it is seen they are problems that on one hand involve operations that need much
calculation and time of processing and on the other they involve operations of interpolation
of functions.
At the present all these cases are solved with other techniques that are commonly
used by mathematicians and engineers. The interesting thing of this project is to be able to
have same the results, if possible, with numerous advantages, applying the algorithm FFT,
such as more speed in the calculation. Nevertheless, the application of Fourier to these
problems is not used and in addition they are of very recent discovery, therefore there is no
pedagogical explanation of them. As a result, this will become in extra work in the project.
All of it will be to programmed in a mathematical tool of last generation, very
commonly used in the academic and investigation scopes, called Matlab. This application
has numerous bookstores with more than three hundred functions enabling it to make any
calculation, one of those bookstores is the FFTW which contains the algorithm of the FFT
and will help us in the calculation of the diverse modules that will be programmed. In
addition, Matlab has an interface GUIDE which is able to program user interfaces in a
simpler way.
In order to develop all this it has not been possible to follow a typical methodology
used to program computer science applications, as Yourdon, but a more suitable has been
used; one that brings together the methodology mentioned before and the following which
VII
Proyecto Fin de Carrera
is frequently used for mathematical projects, which is summed up below:
- Firstly search of documentation.
- Together with step one; there will be a study of each problem.
-Then obtained in the end a list of requirements.
- Third a pseudocode will be done of the problems, programming them on Matlab
and solving them with problems that will serve as tests.
- Next when all the modules are finished, a study of architecture and an external
design of the interface will begin.
- Finally the graphic user interface will be programmed.
To conclude, we will work in an installation guide where we will easily explain
how to install and execute, so that the end user does not have any problem.
VIII
Software de Aplicación de la FFT
Índice
Dedicatoria ...................................................................................................................
I
Agradecimientos...........................................................................................................
II
Resumen....................................................................................................................... III
Abstract......................................................................................................................... VI
Índice............................................................................................................................ IX
1. Introducción y motivación.......................................................................................
.
1
2. Objetivos del proyecto.............................................................................................. 3
3. Análisis de requisitos................................................................................................ 7
3.1. Requisitos funcionales.................................................................................... 7
3.2. Requisitos mantenimiento.............................................................................. 16
3.3. Requisitos de fiabilidad.................................................................................. 17
4. Metodología.............................................................................................................. 18
5. Multiplicación de polinomios................................................................................... 26
5.1. Convolución.................................................................................................... 26
5.2. Multiplicación de polinomios......................................................................... 29
6. Multiplicación de enteros grandes............................................................................ 34
6.1. Multiplicación de enteros............................................................................... 34
7. Interpolación trigonométrica.................................................................................... 40
7.1. Interpolación trigonométrica.......................................................................... 40
8. Aproximación de Chebyshev.................................................................................... 52
8.1. Polinomios de Chebyshev y nodos de Chebyshev......................................... 52
8.2. Aproximación de Chebyshev.......................................................................... 53
9. Estudio de arquitectura............................................................................................. 64
9.1. Especificación de alternativa-1....................................................................... 65
9.2. Especificación de alternativa-2....................................................................... 66
9.3. Valoración de alternativas.............................................................................. 68
IX
Proyecto Fin de Carrera
9.3.1. Matriz de evaluación operativa............................................................. 69
9.3.2. Matriz de evaluación técnica................................................................ 70
9.3.3. Matriz de evaluación económica.......................................................... 71
9.3.4. Valoración final de cada alternativa..................................................... 72
9.4. Elección de alternativa.................................................................................... 72
9.5. Planificación temporal del proyecto............................................................... 73
10. Diseño externo........................................................................................................ 75
10.1. Diseño de ventanas....................................................................................... 75
11. Valoración económica............................................................................................ 88
11.1. Introducción................................................................................................... 88
11.2. Técnicas de estimación de costes................................................................. 88
11.3. Costes del proyecto....................................................................................... 91
12. Conclusiones y líneas futuras................................................................................. 93
13. Bibliografía............................................................................................................. 98
Anexo I. Programación y guía de instalación...............................................................101
I.1. Bibliotecas y Funciones MATLAB.................................................................102
I.2. Guía de instalación del software.....................................................................105
CD-ROM con la aplicación y el código de los algoritmos numéricos del Software de
aplicación de la Transformada Rápida de Fourier (FFT).
X
Software de Aplicación de la FFT
1. Introducción y motivación
La Transformada Rápida de Fourier (Fast Fourier Transform) (FFT) es un
algoritmo eficiente OH log L para calcular la DFT (Transformada Discreta de Fourier).
Originalmente descubierta por Gauss a principios de 1800, basándose en la descomposición
de señales en armónicos simples ideando un algoritmo que podía descomponer señales y
verlas según el dominio de la frecuencia trabajando con ellas, no como fluctuaciones en el
tiempo, sino como señales más simples, cada uno de una frecuencia diferente.
Redescubierta por Cooley y Tukey en IBM durante 1960. La FFT explota las simetrías en la
matriz de Fourier HWL y el teorema de la duplicación basado en el lema de DanielsonLanczos.
Hoy en día la Transformada Rápida de Fourier es de gran importancia en una
amplia variedad de aplicaciones, desde el tratamiento de señales digitales, como por
ejemplo analizar la frecuencia independientemente de la señal que sea, reducción del ruido
de las señales, tratamiento de imagen JPEG y audio como es el caso del MP3, solucionar
ecuaciones diferenciales parciales (aquellas funciones que contienen derivadas con respecto
a dos o más variables), multiplicación rápida de números y polinomios grandes, para los
algoritmos de convolución y desconvolución (operador matemático que transforma dos
funciones f y g en una tercera función que en cierto sentido representa la magnitud en la que
se superponen, f y una versión trasladada e invertida de g) usado para operaciones
1
Proyecto Fin de Carrera
estadísticas como el promedio móvil ponderado. Se emplea en el campo de la óptica
(dispositivos ópticos 2 D y 3 D), en la ingeniería eléctrica se usa para hallar la salida de un
sistema lineal, en la Física allí donde haya un sistema lineal con un "principio de
superposición". Como se ve el algoritmo FFT sirve para explicar y solucionar multitud de
situaciones en casi todos los campos de la ciencia moderna.
La motivación del presente proyecto es realizar un software sencillo e intuitivo
capaz de emplear la FFT para realizar diferentes funciones que incorpore los algoritmos que
permiten solucionar los problemas científicos antes citados, como multiplicar polinomios
de grado alto, resolver ecuaciones diferenciales parciales, determinar los coeficientes de
Fourier y de los polinomios trigonométricos, así como el análisis y procesamiento de
señales digitales. Otra de las motivaciones es el aprendizaje de programación en la
herramienta matemática MATLAB ya que es un lenguaje desconocido y poco utilizado,
pero con gran interés para las empresas por su potencia y funcionalidades por eso en la
actualidad es de los más demandados. El conocimiento y estudio de la FFT es otra de las
motivaciones del proyecto, un algoritmo poco conocido y cuya aplicación a los distintos
campos de la ciencia se han descubierto muy recientemente a lo largo del siglo XX. Por
último señalar que gracias al estudio de todo lo que se ha dicho anteriormente se ampliarán
los conocimientos de matemáticas y métodos numéricos del estudiante.
2
Software de Aplicación de la FFT
2. Objetivos del proyecto
El proyecto se inició con unos objetivos que en la medida que el tiempo ha dejado
se han cumplido prácticamente en su totalidad. La principal intención del proyecto ha sido
la educativa, y la de conocer poco a poco durante el curso, en mayor medida no solo la
transformada de Fourier, sino las diferentes aplicaciones donde se puede aplicar, siendo un
trabajo costoso y complejo, intentando mostrar a través de un software finalmente sus
diferentes opciones de la manera más sencilla posible.
A continuación, se comentan los objetivos del proyecto y en qué nivel se han visto
satisfechos.
1º.
El principal objetivo de este proyecto será diseñar una aplicación informática para
Windows XP/Vista que aplique los diferentes algoritmos de la transformada rápida de
Fourier (FFT), con el fin de realizar de manera práctica las funciones u operaciones que se
explicarán posteriormente y que se han programado en módulos separados. Además la
aplicación, desde el lenguaje de MATLAB, utilizará los algoritmos de la biblioteca de
funciones FFTW para el cálculo de la transformada rápida de Fourier (FFT) en una o
varias dimensiones, de tamaño arbitrario, y empleará estos algoritmos para el cálculo y
aplicación en las materias reseñadas.
3
Proyecto Fin de Carrera
1.1.
El estudio de la multiplicación de polinomios a través de la FFT, a simple vista
parece un tema muy simple, pero se trata de conseguir multiplicar dos polinomios de grado
elevado utilizando la técnica de convolución, explicando antes de modo didáctico qué es la
convolución, tratando de ir desvelando la relación que existe entre ésta y la multiplicación
de polinomios. Hay que destacar que MATLAB no trabaja directamente con polinomios
sino que funciona con matrices. Esto que puede resultar una barrera o una limitación, en
este caso, al final no lo es tanto, ya que la convolución se define de forma matricial,
pudiéndose programar fácilmente con ayuda de la FFT este módulo.
1.2.
El estudio de la multiplicación de enteros de gran magnitud a través de la FFT,
utilizando la convolución otra vez como herramienta principal. El objetivo del módulo es
multiplicar dos números enteros de gran longitud, para la utilización futura como por
ejemplo en el campo de cifrado de documentos. Comentar que este módulo sigue la misma
filosofía de trabajo que el anterior, además no se han encontrado tanto estudios como
documentación donde se demuestre de forma didáctica y aplicada este tema, solamente
encontrándose formulación matemática, consiguiéndose con éxito tras finalizar este módulo
ver de forma sencilla, el funcionamiento de la convolución y su aplicación para así poderse
usar de base para futuros trabajos relacionados.
1.3.
Otro de los módulos tratará sobre la Interpolación Trigonométrica. Con ayuda de
la FFT se podrá aproximar una función dada por medio del polinomio trigonométrico
4
Software de Aplicación de la FFT
interpolador, calculándose de forma separada y diferente sus coeficientes tanto ai como bi ,
necesarios para la interpolación, según en el intervalo en el que se encuentre la función. El
algoritmo podrá interpolar en dos intervalos, tanto en @-p , pD como en @0 , 2 pD. De este
tema es posible encontrar abundante documentación, pero no así su relación con la FFT,
siendo costoso su estudio.
1.4.
La aproximación rápida de Chebyshev es uno de los módulos más interesantes,
gracias a una función llamada Trasformada rápida del coseno (CDT), muy cercana a la
FFT, pudiéndose programar la CDT a través de la trasformada rápida de Fourier, calculando
los coeficientes de Chebyshev de forma fácil y sencilla, con ellos y los famosos polinomios
de Chebyshev se hará una interpolación y por consiguiente una aproximación rápida a una
función continua dada, todo ello en el intervalo @-1 , 1D, haciendo una trasformación si es
necesario si la función se encuentra definida en otro intervalo cualquiera. Reseñándose que
de este tema no hay ninguna documentación al respecto solo encontrándose mencionado en
un par escaso de libros.
2º.
Proponer y realizar distintos problemas de prueba que servirán como ejemplos de
utilización de los distintos algoritmos después de cada explicación teórica del caso y de su
correspondiente pseudocódigo. Cada módulo dispone de una serie de problemas resueltos
como ejemplo de su utilización, con una serie de explicaciones de cómo funciona.
5
Proyecto Fin de Carrera
3º.
Desarrollar una GUI (Interfaz Gráfica de Usuario) para la aplicación. La interfaz
permite ejecutar los algoritmos en un ambiente más amigable para el usuario gracias a la
herramienta que MATLAB posee llamada GUIDE, consiguiéndose así hacer una aplicación
de manejo sencillo que se espera que pueda tener un buen uso didáctico, incluso sin tener
grandes conocimientos de MATLAB. La dificultad en este objetivo ha sido la programación
de la GUI en MATLAB, debido a la escasa documentación en este apartado ya que esta
herramienta matemática no se utiliza principalmente para hacer interfaces graficas, pero sí
ha sido sencillo acoplar en esa interfaz los diferentes módulos que anteriormente se
diseñaron y se programaron con MATLAB.
6
Software de Aplicación de la FFT
3. Análisis de requisitos
3.1 Requisitos funcionales
Prioridad Alta
RF001. Diseñar Interfaz de Usuario.
Se desea diseñar una interfaz de usuario, sencilla e intuitiva, para que la puedan
utilizar usuarios que no entiendan MATLAB, pero que sí tengan conocimiento de
matemáticas u otras ciencias relacionadas con los módulos.
RF001.1. Diseñar ventana de inicio de aplicación.
En la ventana de inicio estarán todos los botones para acceder a los módulos de la
aplicación, con la explicación de lo que hace cada uno de ellos.
Requisitos relacionados:
RF001
RF001.2. Diseñar ventana módulo multiplicación de polinomios.
En la ventana de este módulo se dispondrá de cajas de textos para que se puedan
introducir los datos. En este caso el usuario introducirá en dos pestañas de texto los
polinomios a multiplicar. La solución aparecerá en otro cuadro, y si el usuario quisiera ver
la operaciones intermedias, podrá hacerlo viendo otro cuadro que no será visible por
defecto. Todo estará perfectamente distribuido y explicado con ventanas de información
para orientar al usuario en todo momento.
7
Proyecto Fin de Carrera
Requisitos relacionados:
RF001
RF001.3. Diseñar ventana módulo multiplicación de enteros.
En la ventana de este módulo se dispondrá de cajas de textos para que se puedan
introducir los datos. En este caso el usuario introducirá en dos pestañas los dos números
enteros grandes a multiplicar. La solución aparecerá en otro cuadro de texto. Si el usuario
quisiera ver la operaciones intermedias, podrá hacerlo viendo otro cuadro que no será
visible por defecto. Todo ello estará perfectamente distribuido y explicado con ventanas de
información para orientar al usuario en todo momento.
Requisitos relacionados:
RF001
RF001.4. Diseñar ventana módulo Interpolación trigonométrica.
En la ventana de este módulo, se podrá escribir la función a interpolar en un cuadro
de texto, antes el usuario deberá marcar una opción, entre introducir la función en forma de
vector o en forma normal, acompañado con el número de puntos de la interpolación.
También se tendrá que elegir el intervalo, según sea @-p , pD o @0 , 2 pD. Al hacer la
interpolación saldrá el resultado y además un grafico que mostrará la aproximación,
mostrándose la función que se ha introducido junto a la nueva. Las operaciones intermedias
no serán visibles por defecto pero se podrán ver si el usuario así lo desea.
Requisitos relacionados:
RF001
RF001.5. Diseñar ventana módulo Aproximación rápida de Chebychev.
8
Software de Aplicación de la FFT
Se dispondrá en esta ventana de un cuadro donde se escribirá la función que se
desea aproximar por Chebyshev, además de indicar el intervalo y el número de puntos
escogidos también. El módulo dará como resultado la función que se aproximará a la
propuesta. Esto se podrá ver en una gráfica donde se representarán la función original y la
interpolada por Chebyshev. Las operaciones intermedias no serán visibles por defecto pero
se podrán ver si el usuario así lo desea.
Requisitos relacionados:
RF001
RF002. Diseñar módulos de aplicación.
La aplicación constará de cuatro módulos que se diseñarán de manera
independiente, cada módulo podrá ejecutarse de manera individual, viendo los resultados
fácilmente. Cada vez que un módulo se haya terminado, se diseñará su interfaz,
implantándola después en el programa principal.
RF002.1. Diseñar módulo multiplicación de polinomios.
Se diseñará el módulo teniendo en cuenta no solo que los polinomios se
introducirán en forma de vector, sino que al final se tendrá que trasformar el vector
resultante de la multiplicación en forma polinómica para que el usuario pueda verlo de
forma sencilla. En este módulo no solo se ha tenido en cuenta el uso de la función fft y la
propiedad de la convolución, sino que desde el principio los resultados se meterán todos en
un fichero de texto, para en un futuro visualizarlos en una interfaz gráfica, por ello se va a
tener que hacer una parte del diseño para poder trasformar el resultado que será un
9
Proyecto Fin de Carrera
polinomio, en forma de string, ya que el módulo trabajará con variables simbólicas, y por
limitaciones del software de programación, en este caso MATLAB, es imposible grabar en
un fichero variables de este tipo.
Requisitos relacionados:
RF002
RF002.2. Diseñar módulo multiplicación de enteros.
Al diseñarse el módulo de multiplicación de enteros, se tienen que tener en cuenta
dos factores. Uno es que los números dados van a ir en formato string y por consiguiente se
van a tener que pasar a vectores de formato long. El segundo es que los vectores tienen que
operarse de forma inversa teniendo que hacer estas dos cosas en una función aparte, que se
explicará a continuación. En este módulo se utilizará la función fft y la propiedad de la
convolución y además el paso de todos los resultados a fichero de texto para que en un
futuro se visualicen en una interfaz gráfica.
Requisitos relacionados:
RF002
RF002.2.1. Diseñar módulo cadena a enteros.
Se programará un sencillo módulo para pasar las cadenas de números enteros en
forma de string a formato long, transformándose el vector, poniendo las coordenadas de
forma inversa y devolviendo el resultado para las futuras operaciones.
Requisitos relacionados:
RF002.2
RF002.3. Diseñar módulo Interpolación trigonométrica.
10
Software de Aplicación de la FFT
Se diseñará y programará un módulo de interpolación trigonométrica donde el
usuario podrá hacer la interpolación introduciendo una función continua o un vector de
coordenadas pares correspondientes a los valores de una función. Según se haya introducido
un intervalo u otro @-p, pD o @0, 2 pD el algoritmo hará operaciones diferentes, llamando al
final al algoritmo de la fft para realizar los cálculos necesarios. Por último, se tendrá que
introducir el número de puntos de la interpolación, siempre un número par de puntos. Se
obtendrá al final el polinomios interpolador, guardando todas las operaciones relevantes en
un archivo de texto para su futura visualización.
Requisitos relacionados:
RF002
RF002.4. Diseñar módulo Aproximación de Chebychev.
Se programará un algoritmo capaz de calcular la aproximación rápida de
Chebyshev. El usuario tendrá que introducir una función continua, junto con su intervalo
@-1, 1D. Si no se introduce ese intervalo el algoritmo reajustará el intervalo para que valga.
Por último, se introducirá el número de puntos. Utilizando la función de la DCT
(trasformada discreta del coseno) con FFT, se calcularán los coeficientes de Chebyshev, y
tras esto se llamará a otra función que calculará los polinomios de Chebyshev. El resultado
será el polinomio de aproximación de Chebyshev. Todas las operaciones intermedias se
guardarán en fichero de texto para futuras visualizaciones.
Requisitos relacionados:
RF002
RF002.4.1. Diseñar módulo polinomios de Chebychev.
11
Proyecto Fin de Carrera
Se introducirá en este módulo el grado del polinomio de Chebyshev, y el módulo
calculará el polinomio de ese grado, devolviendo el resultado para utilizarlo en el módulo
de aproximación rápida de Chebyshev.
Requisitos relacionados:
RF002.4
RF002.4.2. Diseñar módulo DCT con FFT.
Se sabe que la Trasformada discreta del coseno tiene relación con la Trasformada
discreta de Fourier. Sabiendo esto se diseñará un algoritmo capaz de conseguir la DCT de
un vector dado llamando a la función fft que posee MATLAB.
Requisitos relacionados:
RF002.4
Prioridad Media
RF003. Mostrar gráficas de los resultados obtenidos.
En las ventanas de los módulos de aproximación rápida de Chebyshev y de
Interpolación Trigonométrica es interesante no solo poder ver las operaciones intermedias
que hace el algoritmo y el resultado final, sino poder observar en una gráfica las
aproximaciones, con la función original. Se va a introducir en la ventana de dichos módulos
un apartado para ver los resultados de forma grafica, de manera sencilla y simple.
Requisitos relacionados:
RF001.4
Requisitos relacionados:
RF001.5
12
Software de Aplicación de la FFT
RF004. Mostrar ventana información sobre funciones en MATLAB.
En los módulos de aproximación rápida de Chebyshev y de Interpolación
Trigonométrica se pondrá en la ventana del interfaz del usuario un botón de información.
En estos módulos se introduce una función como datos de entrada, pero al hacerse pueden
quedar dudas de cómo se escriben algunas expresiones en el lenguaje MATLAB. Para
ayudar al usuario y remediar posibles fallos en su escritura se diseñará una ventana
informativa que el usuario podrá consultar en todo momento, viendo en ella de forma clara
cómo se escriben las expresiones en MATLAB y solucionar así cualquier problema que
pueda surgir.
Requisitos relacionados:
RF001.4
Requisitos relacionados:
RF001.5
RF005. Mostrar ayuda de la ventana de menú.
Se diseñará una pequeña ventana de ayuda que se visualizará al apretar un botón de
información en la ventana principal de la aplicación, orientando al usuario y diciéndole qué
posibles acciones puede hacer y así ser más cómoda la navegación por la interfaz desde el
principio.
Requisitos relacionados:
RF001.1
RF006. Mostrar ayuda de la ventana de Multiplicación de enteros.
Se diseñará una pequeña ventana de ayuda que se visualizará al apretar un botón de
13
Proyecto Fin de Carrera
ayuda en la ventana de Multiplicación de enteros, guiando paso a paso al usuario. Será una
guía de usuario pero de forma simplificada, con la información ordenada para que el
usuario al leerla solo una vez, pueda saber qué hacer en el módulo, manejando la aplicación
con soltura desde el primer momento.
Requisitos realacionados: RF001.2
RF007. Mostrar ayuda de la ventana de Multiplicación de polinomios.
Se diseñará una pequeña ventana de ayuda que se visualizará al apretar un botón de
ayuda en la ventana de Multiplicación de polinomios, guiando paso a paso al usuario. Será
una guía de usuario pero de forma simplificada, con la información ordenada para que el
usuario al leerla solo una vez, pueda saber qué hacer en el módulo, manejando la aplicación
con soltura desde el primer momento.
Requisitos relacionados:
RF001.3
RF008. Mostrar ayuda de la ventana de Interpolación Trigonométrica.
Se diseñará una pequeña ventana de ayuda que se visualizará al apretar un botón de
ayuda en la ventana de Interpolación Trigonométrica, guiando paso a paso al usuario. Será
una guía de usuario pero de forma simplificada, con la información ordenada para que el
usuario al leerla solo una vez, pueda saber qué hacer en el módulo, manejando la aplicación
con soltura desde el primer momento.
Requisitos relacionados:
RF001.4
14
Software de Aplicación de la FFT
RF009. Mostrar ayuda de la ventana de Aproximación rápida de Chebyshev.
Se diseñará una pequeña ventana de ayuda que se visualizará al apretar un botón de
ayuda en la ventana de Aproximación rápida de Chebyshev, guiando paso a paso al usuario.
Será una guía de usuario pero de forma simplificada, con la información ordenada para que
el usuario al leerla solo una vez, pueda saber qué hacer en el módulo, manejando la
aplicación con soltura desde el primer momento.
Requisitos relacionados:
RF001.5
RF010. Mostrar ventana de Error.
Se diseñará una pequeña ventana de Error para los módulos de la aplicación que
sean necesarios, avisando al usuario de que ha ocurrido durante el trascurso de las
operaciones algún fallo, cometido por introducirse erróneamente un dato de entrada. Se
informará detalladamente el fallo escribiéndose el fichero de texto que creará el módulo
para que el usuario pueda verlo en la ventana de operaciones.
Requisitos relacionados:
RFI001
RF011. Guardar resultados en ficheros Matlab.
Se programarán los módulos de tal forma que los resultados se guardarán en
ficheros de texto para su utilización en las salidas de la interfaz gráfica o para que el usuario
pueda guardar una vez finalizados los cálculos los resultados para poder utilizarlos en
acciones futuras. Se crearán los ficheros de manera que se podrá actualizar cada vez que se
haga una nueva operación, no borrándose lo anterior. Cada módulo posee su fichero de
15
Proyecto Fin de Carrera
texto individual.
Requisitos realacionados: RF001.2
Requisitos realacionados: RF001.3
Requisitos realacionados: RF001.4
Requisitos realacionados: RF001.5
3.2 Requisitos mantenimiento
Prioridad alta
RM001. Crear guía de instalación y usuario.
Se creará dentro del proyecto una guía de instalación y de usuario ya que se pueden
encontrar posibles problemas al instalar el software MATLAB. Además aunque la
aplicación se ha pensado de manera que para el usuario sea lo más sencilla posible se
pondrá una breve guía resolviéndose así todas las dudas posibles.
16
Software de Aplicación de la FFT
3.3 Requisitos de fiabilidad
Prioridad alta
RFI001. Verificación de los datos de entrada.
Se programarán los módulos para que el usuario no pueda introducir datos de
entrada erróneos, validándolos y avisándose seguidamente si el usuario introduce una
variable incorrecta por medio de una ventana de diálogo.
Requisitos relacionados:
RF001.2
Requisitos relacionados:
RF001.3
Requisitos relacionados:
RF001.4
Requisitos relacionados:
RF001.5
17
Proyecto Fin de Carrera
4. Metodología
Dado que el proyecto que se presenta no es un desarrollo de software estándar sino
una aplicación matemática, para el cual un ingeniero en informática se podría valer de
metodologías de ingeniería del software clásicas, en este caso el proyecto ha obligado a
definir una metodología distinta para el diseño y programación de los diferentes módulos.
En parte porque para afrontar la parte de diseño de la interfaz gráfica se ha seguido un
modelo estructurado de Yourdon, que es el caso clásico en el diseño de una aplicación
informática, pero solo aplicando algunas fases ya que esta metodologia posee fases que en
este proyecto no tiene sentido hacerlas. Se han intentado seguir unos pasos formales y la
metodología resultante se mostrará a continuación. Se han estipulado los paquetes de
trabajo que se indican más adelante, además de venir definidas qué tareas se va a realizar en
cada caso.
18
Software de Aplicación de la FFT
Software de
aplicación
de la FFT
WP 00
WP 01
WP 02
Gestión
Conceptos
Codificación
Pruebas
Creación
Generales
Algoritmos
de Algoritmo
GUI
WP 02.1
Programación
WP 03
WP 04
WP 05
Conclusiones
WP 03.1
Generación
de Problemas
WP 04.1
WP 04.2
Estudio de
Diseño Externo
WP 01.1
WP 01.2
WP 01.3
WP 01.4
Búsqueda de
Identificación
Análisis de
Diseñar
información
de Necesidades
Requisitos
Arquitectura
Pseudocódico
WP.00 - Gestión
Definición: El paquete de Gestión no se refiere a una tarea que tardará un tiempo
determinado, sino que durará todo desarrollo del proyecto hasta su finalización. Se trata de
las diferentes entrevistas que se producirán a lo largo del ciclo del diseño del proyecto,
programando reuniones semanales o quincenales, vigilando con esto la correcta realización
de los contenidos del proyecto. Así mismo, se incluye en este paquete todo el trabajo que
tenga que ver con el seguimiento del correcto funcionamiento del proyecto, como por
19
Proyecto Fin de Carrera
ejemplo las fases de pruebas finales.
Entradas: Entregables del proyecto en distintas fases de realización.
Salidas: Las entradas revisadas y modificadas si se creyera necesario.
WP.01.1 - Búsqueda de la información
Definición: Antes de empezar a diseñar y programar nada se tendrá que estudiar el
tema tanto de la Trasformada rápida de Fourier como del lenguaje MATLAB con el que se
va a programar y las diferentes herramientas auxiliares para realizar la documentación. La
información se ha buscado tanto en bibliotecas; publicaciones de libros y ensayos
matemáticos y de telecomunicaciones, como en Internet, siendo esta última fuente de poca
ayuda. Al contrario de lo que cabría esperar ya que todas las publicaciones ubicadas en
Internet son de uso privado y restringido, por lo tanto inaccesibles.
Entradas: No hay entradas ya que se trata solo de la búsqueda de información.
Salidas: Será la información necesaria para poder empezar a diseñar los módulos de
la aplicación.
WP.01.2 - Identificación de necesidades
Definición: Se trata de uno de los procesos en el ciclo de desarrollo de una
aplicación en Yourdon. Una vez obtenida la información y estudiándose toda la teoría
matemática a fondo, se procederá a identificar las necesidades del usuario que en un
20
Software de Aplicación de la FFT
principio utilizaría la aplicación, con ayuda de las entrevistas semanales se acotará el
entorno global del problema en estudio, produciéndose al final los objetivos generales del
sistema.
Entradas: Se tendrán en cuenta todas la ideas y propuestas que tenga el posible
usuario que utilizará en un futuro la aplicación.
Salidas: Serán los objetivos concretos del proyecto, el alcance, tipología de
usuarios finales, restricciones, produciendo lo que se llama, documento de conceptos del
sistema, que en el proyecto se ha denominado objetivos.
WP.01.3 - Análisis de requisitos
Definición: Una vez terminado el documento de conceptos del sistema se procederá
al análisis de requisitos, en él se escribirá y analizará todo lo que el sistema hará, una vez se
finalice el proyecto. Teniendo el alcance y los objetivos se clasificarán según su prioridad y
la tipología del requisito. Esta parte del proyecto es una de las más importantes ya que todo
lo que se apruebe aquí, será la columna vertebral del proyecto, teniendo en cuenta esto a lo
largo de su diseño y desarrollo.
Entradas: Se utilizarán los objetivos que se han obtenido antes en el módulo
anterior como punto de partida.
Salidas: Será la lista de requisitos y la estructura de los módulos para su posterior
21
Proyecto Fin de Carrera
diseño y programación.
WP.01.4 - Diseñar pseudocódigo
Definición: Se diseñará cada módulo en pseudocódigo cumpliendo con los
requisitos antes citados. Cuando se termine cada pseudocódigo se revisará, se corregirá y se
pasará a la siguiente fase del ciclo de vida del proyecto, así con cada uno de los módulos.
Usando un lenguaje en pseudocódigo fácil e intuitivo, basándonos en la teoría matemática
se harán los diferentes algoritmos para después programarlos.
Entradas: Se dispondrá de los requisitos y los documentos de teoría matemática
que explican cada uno de los diferentes métodos de utilización de la FFT.
Salidas: Como salida se tendrán los diseños en pseudocódigo para finalmente
implantarlo en la programación.
WP.02.1 - Programación
Definición: Cuando se diseñe y finalice el pseudocódigo se programará el algoritmo
en lenguaje MATLAB, programando también un código de prueba junto a él para poderse
probar y saber si funciona de manera satisfactoria.
Entradas: Basándose en los pseudocódigos se programarán los módulos.
Salidas: Como salida se tendrá los módulos programados en MATLAB junto a los
ficheros también en MATLAB de prueba, para saber si los cálculos se hacen correctamente
22
Software de Aplicación de la FFT
y poder modificarse si fuera necesario.
WP.03.1 - Generación de problemas
Definición: Para poder probar los algoritmos, además de los ficheros MATLAB de
prueba iniciales se dispondrá de diferentes problemas sacados de diferentes libros de
Métodos Numéricos, con diferentes datos para poder saber si los módulos funcionan en
todas sus casuísticas, cambiando y modificando los programas en caso de errores en su
funcionamiento y volviendo a diseñar el pseudocódigo.
Entradas: Como entrada se tendrá tanto los módulos programados como los
diferentes problemas planteados.
Salidas: Como salida se tendrá los resultados junto con los errores, que se
considerarán las pruebas de la aplicación. Con ellas se mejorará el rendimiento de la
aplicación y se eliminarán posibles defectos.
WP.04.1 - Diseño externo
Definición: Dentro del diseño externo se tendrá especial atención en el diseño de
entradas, es decir, en el diseño y programación de cada una de las ventanas de la aplicación,
una vez terminado todas las programaciones de los módulos en MATLAB. Se programarán
las ventanas en MATLAB con la herramienta GUIDE, para hacer una interfaz de usuario
intuitiva y sencilla.
Entradas: Se dispondrá de los módulos en MATLAB junto con el análisis de
23
Proyecto Fin de Carrera
requisitos para saber cómo se diseñarán las ventanas de la interfaz de usuario.
Salidas: Como salida se tendrán los diseños de las ventanas de cada módulo, para
programarlas en GUIDE.
WP.04.2 - Estudio de arquitectura
Definición: En esta fase se estudiará el último punto del método de Yourdon que se
utilizará para seguir la metodología de diseño de una aplicación informática. En el estudio
de arquitectura se tendrá el estudio de las diferentes alternativas de implantación de la
aplicación. Poniendo la mejor alternativa que se utilizar a posteriori tanto Hardware como
Software. En esta parte también se tendrá en cuenta la planificación que se ha seguido
durante todo el año.
Entradas: Tanto los requisitos como la información sobre las diferentes
alternativas en la implantación a utilizar.
Salidas: Especificación lógica de la solución elegida y Planificación del proyecto a
desarrollar.
WP.05 - Conclusiones
Definición: En esta fase se redactarán las conclusiones del proyecto. Se intentará
que no tengan un nivel muy avanzado y que sean de fácil comprensión con un lenguaje
adaptado a personas que no necesariamente tengan que estar muy preparadas en el campo
de la transformada de Fourier. El contenido de estas conclusiones será el grado de
24
Software de Aplicación de la FFT
cumplimiento de los objetivos y las dificultades que se han tenido al realizar las diferentes
aplicaciones del algoritmo de Fourier y las posibles mejoras y añadidos que en un futuro
podría tener la aplicación.
Entradas: Toda la información generada a lo largo del proyecto.
Salidas: El apartado de conclusiones del proyecto.
25
Proyecto Fin de Carrera
5. Multiplicación de polinomios
5.1 Convolución
1. Definicion de Convolución y Producto de Convolución discreta de
vectores.
Sean x, y dos vectores de dimensión . El producto de convolución se define
como el vector x * y:
x* y =
x0
x1
x2
x3
...
x-2
x-1
x -1
x0
x1
x2
...
x -3
x -2
x -2
x -1
x0
x1
...
x -4
x -3
...
...
...
...
...
...
...
x2 x1
y0
x3 x2
y1
x4 x3
y2
x5 x4 . y3
... ...
...
x0 x -1
y -2
x1 x0
y -1
(1)
La n - ésima componente del producto de convolución x * y viene dado por las
expresiones
Hx * yLn =
y0 xn + y1 xn-1 + ... + yn x0 + yn+1 x -1 + ... + y-1 xn+1 ,
n
-1
j=0
j=n+1
Hx * yLn = ‚ y j xn- j + ‚ y j x +n- j =
‚ y j xk +
j+k=n
‚
y j xk .
j+k=+1
26
(2)
Software de Aplicación de la FFT
La matriz cuadrada anterior se la llama circulante (los elementos de la primera
columna rotan su posición en las columnas sucesivas). También se puede ver que la primera
columna es el vector x y que posee una diagonal constante y en cada diagonal paralela a ella
todos los elementos son iguales.
Por tanto, se puede expresar el producto de convolución como:
x * y = C HxL y
(3)
donde C HxL es la matriz circulante generada por x.
Además existe una relación entre las matrices circulantes y la transformada discreta
de Fourier.
Siendo C HxL matriz circulante, como consecuencia es diagonalizable (una matriz
A œ Mn de dimensión n x n es diagonalizable si existe una matriz P œ Mn , denominada de
paso, inversible tal que P-1 A P = D es diagonal) tomando como matriz de paso , se dice
que:
H L-1 C HxL = L
(4)
siendo L la matriz de autovalores formada por una matriz diagonal cuyos elementos
diagonales son en el mismo orden los de b = DFT HxL. Es decir, L = diagH bi L. Operando
resulta:
C HxL = L C HxL = LH L-1
1
C HxL =
L (5)
Con esto se pasa a ver un teorema que permite calcular el producto de convolución
empleando la transformada discreta de Fourier.
27
Proyecto Fin de Carrera
ô Teorema 1. Producto de Hadamard ( b.g)
Sean
las
transformadas
discretas
de
Fourier
b = DFT HyL = y
y
g = DFT HzL = z, entonces el producto de convolución x * y será:
y * z = C HyL z =
1
L z =
1
L g
Con esto y viendo como es la estructura de b, L = diagH bi L y del vector g se dice
que el producto L g es un vector que se obtiene multiplicando b y g coordenada a
coordenada, es decir,
HL gLn = bn gn :
b=
b0
b1
...
b0 0
0 b1
L=
... ...
0 0
,
b -1
b0 0
0 b1
Lg =
... ...
0 0
...
0
...
0
,
... ...
... b -1
g0
g1
g=
,
...
g -1
g0
...
0
b0 g0
g1
...
0
b1 g1
.
=
.
... ...
...
...
... b -1 g -1
b -1 g -1
Como conclusión a esto se dice que para el cálculo del producto de convolución
y * z requiere obtener las DFT de los vectores y y z, se multiplican coordenada a
coordenada, y luego se realiza la transformada inversa de Fourier:
y*z =
1
L g =
1
H b.gL = IDFTH b.gL.
28
(6)
Software de Aplicación de la FFT
5.2 Multiplicación de polinomios
Se emplea la convolución para multiplicar polinomios. Sean los polinomios pHxL de
grado n y qHxL de grado m. El producto pHxL qHxL es otro polinomio de grado n + m cuyos
coeficientes se calculan de la siguiente forma:
1.
En primer lugar se toman los vectores c p y cq que contienen los coeficientes de pHxL
y qHxL respectivamente en potencias decrecientes de x y se rellenan con ceros hasta la
dimensión n + m + 1.
2.
El producto de convolución c p * cq es el vector de los coeficientes de pHxL.qHxL en
potencias decrecientes de x que lo se llamará r. Se toman las transformadas discretas de
Fourier b = DFTHc p L y g = DFT Hcq L, obteniendo:
c p * cq =
1
n+m+1
n+m+1 H b.gL = IDFTH b.gL
c p * cq = Hrn+m , rn+m-1 , ..., r2 , r1 , r0 LT .
Por tanto, si se dispone en forma de polinomio se tiene la expresión:
pHxL qHxL = rn+m xn+m + rn+m-1 xn+m-1 + ... + r2 x2 + r1 x + r0 .
è Algoritmo 1. Multiplicación por convolución de polinomios
grandes.
Multiplicación de
polinomios
H* Los argumentos que recibe la función son y,
29
Proyecto Fin de Carrera
H* Los argumentos que recibe la función son y,
z dos vectores, donde se guardan los coeficientes
de las x de cada polinomio. Se devolverá un polinomio
resultado de la multiplicación realizada con la FFT *L
Input HHyL, Hz LL
H* Declaración variable simbólica*L
x ≠ simbólica HxL
H* Tamaño del primer y segundo vector *L
n ≠ longitud HyL
m ≠ longitud HzL
H* Grado de los vectores *L
grado_ 1 ≠ longitud HyL - 1
grado_ 2 ≠ longitud HzL - 1
H* Tamaño de la matriz inversa de Fourier n+m+1 *L
n+m+1 ≠ n + m + 1
H* Se igualan los tañamos de los vectores, llenándolos con 0 *L
For i = n + 1, n + 2, n + 3, ..., n+m+1 do
yi ≠ 0
End
For i = m + 1, m + 2, m + 3, ..., n+m+1 do
zi ≠ 0
End
H* Se hece la trasformada rápida de Fourier de cada vector *L
bi ≠ fft HyL
gi ≠ fft HzL
H* Se multiplican las dos matrices * L
ai ≠ bi µ gi
H* Se hace la trasformada rápida inversa de Fourier de ai *L
wi ≠ ifft HaL
H* Se eliminan los ceros del final *L
For i = 1, 2, 3, ..., Hgrado_ 1 + grado_ 2L do
Ri ≠ wi
30
Software de Aplicación de la FFT
End
(* Se pasa el vector a forma polinómica *)
For i = 1, 2, 3, ..., Hgrado_ 1 + grado_ 2L do
Fi ≠ Ri * x Hgrado_ 1 + grado_ 2L+1-iL
End
For i = 1, 2, 3, ..., Hgrado_ 1 + grado_ 2L do
End
F ≠ SHFi L
Return HHF L L
Output
à Ejemplo 1. Sean los polinomios pHxL y qHxL dados. Hallar el producto pHxL qHxL
mediante el empleo del producto de convolución.
a)
b)
pHxL = 2 x3 - 3 x2 + x - 55,
pHxL = 4 x3 + 3 x2 + 2 x + 1,
qHxL = x3 + 5 x2 - 10 x + 13.
qHxL = 4 x4 - 3 x3 + 2 x2 - x + 1.
à Solución apartado a)
% Polinomio 1 º H2 ∗ x ^ 3 − 3 ∗ x ^ 2 + x − 55L
y = @2; −3; 1; −55D;
% Polinomio 2 Hx ^ 3 + 5 ∗ x ^ 2 − 10 x + 13L
z = @1; 5; −10; 13D;
X = Multiplicacion_de _Polinomios Hy, zL;
y = 2 − 3 1 − 55 0 0 0 0 0
z = 1 5 − 10 13 0 0 0 0 0
% FFT HyL
Y=
−55.0000
27.3755 + 48.5750 i
28.0394 − 45.0190 i
−52.0000 + 3.4641 i
33.0851 + 49.3002 i
33.0851 − 49.3002 i
−52.0000 − 3.4641 i
31
Proyecto Fin de Carrera
28.0394 + 45.0190 i
27.3755 − 48.5750 i
% FFT HzL
Z=
9.0000
−3.4063 − 4.6242 i
4.7652 + 9.7545 i
16.5000 − 12.9904 i
−17.8589 − 19.3963 i
−17.8589 + 19.3963 i
16.5000 + 12.9904 i
4.7652 − 9.7545 i
−3.4063 + 4.6242 i
% Vector resultante del producto de convolución
R=
2.0000
7.0000
−34.0000
6.0000
−324.0000
563.0000
−715.0000
% Resultado en forma polinómica
6
5
4
3
2
2 x + 7 x − 34 x + 6 x − 324 x + 563 x − 715
à Solución apartado b)
% Polinomio 1 º H4 x ^ 3 + 3 x ^ 2 + 2 x + 1L
y = @4; 3; 2; 1D;
% Polinomio 2 º H4 x ^ 4 − 3 x ^ 3 + 2 x ^ 2 − x + 1L
z = @4; −3; 2; −1; 1D;
X = Multiplicacion_de _Polinomios Hy, zL;
y=4 3 2 1 0 0 0 0 0 0
z = 4 −3 2 −1 1 0 0 0 0 0
% FFT HyL
Y=
10.0000
32
Software de Aplicación de la FFT
6.7361 − 4.6165 i
2.5000 − 3.4410 i
2.2639 − 1.0898 i
2.5000 − 0.8123 i
2.0000
2.5000 + 0.8123 i
2.2639 + 1.0898 i
2.5000 + 3.4410 i
6.7361 + 4.6165 i
% FFT HzL
Z=
3.0000
1.6910 + 0.2245 i
2.5729 + 2.0409 i
2.8090 + 2.4899 i
5.9271 + 5.2043 i
11.0000
5.9271 − 5.2043 i
2.8090 − 2.4899 i
2.5729 − 2.0409 i
1.6910 − 0.2245 i
% Vector resultante del producto de convolución
R=
16.0000
−0.0000
7.0000
0.0000
2.0000
3.0000
1.0000
1.0000
% Resultado en forma polinómica
7
5
3
2
16 x + 7 x + 2 x + 3 x + x + 1
33
Proyecto Fin de Carrera
6. Multiplicación de enteros grandes
6.1 Multiplicación de enteros
Se empleará la convolución para multiplicar enteros de gran tamaño. Sean los
vectores A de dimensión n y B de dimensión m . El producto A B es otro vector C de
dimensión n + m + 1 que tendrá el resultado del producto de convolución expresado de la
forma siguiente:
C0 100 + C1 101 + C2 102 + ... ... .. + Cn-2 10n-2 + Cn-1 10n-1 + Cn 10n .
(7)
Se multiplicarán dos números enteros muy grandes siguiendo los pasos siguientes:
1.
En primer lugar se toman los vectores A y B que contienen las cifras de los números
puestas de forma inversa, es decir las unidades irán en la primera posición del vector, las
decenas en la segunda posición, etc. Se rellenarán con ceros los vectores hasta la dimensión
n + m + 1.
2.
Se usan las transformadas discretas de Fourier b = DFT HAL y g = DFTHBL,
obteniendo:
A*B =
1
n+m+1
n+m+1 Hb.gL = IDFT H b.gL
A * B = HC0 , C1 , ..., Cn-2 , Cn-1 , Cn LT .
Por tanto, dispuesto el resultado en el orden adecuado, se obtiene el número
resultante del producto:
34
Software de Aplicación de la FFT
A B = C0 100 + C1 101 + C2 102 + ... ... .. + Cn-2 10n-2 + Cn-1 10n-1 + Cn 10n .
è Algoritmo 2. Multiplicación por convolución de dos números
enteros grandes.
Multiplicación de números enteros
grandes
H* Los argumentos que recibe la función son y ,
y z que son dos cadenas de caracteres donde se
guardan los dos números. Se devolverá una variable
resultado de la multiplicación realizada con la FFT *L
Input HHyL, Hz LL
H* Se llama a la funcion Cadena_de_Enteros_a_vector
para pasa las dos cadenas de caracteres a vectores *L
Y ≠ Cadena_de _Enteros _a _vector HyL
Z ≠ Cadena_de _Enteros _a _vector HzL
H* Tamaño del primer vector *L
n ≠ longitud HY L
H* Tamaño del segundo vector *L
m ≠ longitudHZ L
H* Tamaño de la matriz Inversa de Fourier n+m+1 *L
n+m+1 ≠ n + m + 1
H* Se igualan los tañamos de los vectores, llenándolos con 0 *L
For i = n + 1, n + 2, n + 3, ..., n+m+1 do
Yi ≠ 0
End
For i = m + 1, m + 2, m + 3, ..., n+m+1 do
Zi ≠ 0
35
Proyecto Fin de Carrera
End
H* Se haca la trasformada rápida de Fourier de cada vector *L
bi ≠ fftHY L
gi ≠ fftHZL
H* Se multiplican las dos matrices *L
ai ≠ bi µ gi
H* Se hace la trasformada rápida inversa de Fourier de ai *L
wi ≠ ifftHaL
H* Se convierte el vector a número *L
For i = 1, 2, 3, ..., n+m+1 do
Ji ≠ wi µ 10i-1
End
For i = 1, 2, 3, ..., Hgrado_ 1 + grado_ 2L do
J ≠ SHJi L
End
Return HJ L
Output
è Algoritmo 3. Conversión de cadena de caracteres a vector.
El argumento que recibe la función y es una cadenas de caracteres donde se guarda
el número. Se devolverá un vector donde se irán guardando las cifras puestas inversamente
del numero dado.
Conversión de cadena de caracteres a vector
Input HHyLL
H* Tamaño de la cadena de caracteres *L
n ≠ longitud HyL
H* Se pasa la cadena al vector llamando a la función str2num.
*L
H* Esta función transforma un caracter yHiL de la cadena a entero. *L
For i = 1, 2, 3, ..., n do
Vi ≠ str2numHyHn - i + 1L
End
36
Software de Aplicación de la FFT
Return HV L
Output
à Ejemplo 2. Sean dos números enteros 2.345.677.889.993.453.465.349 y
35.235.235.252.353.253.255 dados. Hallar el producto mediante el empleo del producto
de convolución.
à Solución
a = ' 2 345 677 889 993 453 465 349 ';
b = ' 35 235 235 252 353 253 255 ';
S = Multiplicacion_de _Enteros Ha, bL;
% FFT HaL
Y=
1.0 e + 002 ∗ 1.2300
−0.0521 − 0.7968 i
−0.0744 + 0.1642 i
0.2159 − 0.1268 i
0.0748 − 0.1188 i
−0.0143 − 0.1135 i
0.0147 + 0.0420 i
0.0932 + 0.0110 i
0.1069 − 0.0313 i
0.0351 − 0.0257 i
0.0848 + 0.0361 i
0.1242 + 0.0130 i
0.1511 − 0.0572 i
0.0587 − 0.0892 i
0.0248 − 0.0358 i
0.0433 + 0.0208 i
0.0920 − 0.0011 i
0.0825 − 0.0193 i
0.0532 − 0.0428 i
0.0307 + 0.0187 i
0.0849 + 0.0184 i
0.0849 − 0.0184 i
0.0307 − 0.0187 i
0.0532 + 0.0428 i
0.0825 + 0.0193 i
0.0920 + 0.0011 i
0.0433 − 0.0208 i
0.0248 + 0.0358 i
0.0587 + 0.0892 i
0.1511 + 0.0572 i
0.1242 − 0.0130 i
37
Proyecto Fin de Carrera
0.0848 − 0.0361 i
0.0351 + 0.0257 i
0.1069 + 0.0313 i
0.0932 − 0.0110 i
0.0147 − 0.0420 i
−0.0143 + 0.1135 i
0.0748 + 0.1188 i
0.2159 + 0.1268 i
−0.0744 − 0.1642 i
−0.0521 + 0.7968 i
% FFT HbL
Z=
70.0000
7.0736 − 43.9634 i
0.5056 − 0.3351 i
6.9568 − 13.6612 i
1.2270 − 0.5053 i
6.8344 − 7.8495 i
1.3599 − 0.0750 i
8.3503 − 5.3707 i
1.0527 − 2.4993 i
5.6105 − 3.3450 i
1.2999 + 1.6988 i
13.3073 − 1.8327 i
2.5414 − 7.7762 i
9.2568 − 2.9295 i
−0.1125 − 15.6934 i
−8.7465 + 1.4154 i
4.6226 + 3.0401 i
3.1238 − 3.4136 i
−1.0351 − 2.3406 i
−0.6865 + 2.9046 i
4.9581 + 2.6797 i
4.9581 − 2.6797 i
−0.6865 − 2.9046 i
−1.0351 + 2.3406 i
3.1238 + 3.4136 i
4.6226 − 3.0401 i
−8.7465 − 1.4154 i
−0.1125 + 15.6934 i
9.2568 + 2.9295 i
2.5414 + 7.7762 i
13.3073 + 1.8327 i
1.2999 − 1.6988 i
5.6105 + 3.3450 i
1.0527 + 2.4993 i
8.3503 + 5.3707 i
1.3599 + 0.0750 i
6.8344 + 7.8495 i
1.2270 + 0.5053 i
38
Software de Aplicación de la FFT
6.9568 + 13.6612 i
0.5056 + 0.3351 i
7.0736 + 43.9634 i
% Resultado del producto de convolución
S = 8.2651 e + 040
39
Proyecto Fin de Carrera
7. Interpolación trigonométrica
7.1 Interpolación trigonométrica
1. Definicion de Polinomio trigonométrico interpolador.
Como se ha comentado anteriormente en la introduccíón una de las aplicaciones
prácticas de la trasformada rápida de Fourier es el cálculo en un periodo T del polinomio
trigonométrico que interpola una función real.
m-1
Se el conjunto de 2 m puntos 8xi , yi <2i=0
que dividen uniformemente el intervalo
cerrado @-p, pD, siendo las abscisas xi :
ip
xi = -p +
m
i = 0, 1, ..., 2 m - 1
(8)
y sus ordenadas yi = f Hxi L. El polinomio trigonométrico interpolador que pasa por estos
puntos de grado m - ésimo tiene la expresión:
Sm HxL =
a0
2
+
am cosHm xL
2
m-1
+ ‚ Hai cosHi xL + bi senHi xLL
(9)
i=1
siendo las constantes 8ai < y 8bi < de Sm HxL
ai =
bi =
1
m
1
m
2 m-1
‚ y j cosHi x j L
j=0
2 m-1
‚ y j senHi x j L
j
Hi = 0, 1, 2, ..., mL
(10)
Hi = 1, 2, ..., m - 1L.
Descripción de cálculo de los coeficientes del polinomio trigonométrico en
[-p, p]
40
Software de Aplicación de la FFT
El polinomio trigonométrico que interpola = 2 m = 2 p puntos en @-p, pD tiene la
expresión:
Sm HxL =
ai =
bi =
1
m
1
m
a0
2
+
am cosHm xL
2
2 m-1
‚ y j cosHi x j L
j=0
2 m-1
‚ y j senHi x j L
j=0
m-1
+ ‚ Hai cosHi xL + bi senHi xLL,
i=1
Hi = 0, 1, 2, ..., mL
(11)
Hi = 1, 2, ..., m - 1L.
Para poder calcular los coeficientes 8ai < y 8bi < del polinomio trigonométrico
interpolador nos tendremos que basar en el algoritmo de la transformada rápida de Fourier
HFFT L o método de Cooley-Tukey.
ô Teorema 2. Método de Cooley-Tukey
El método consiste en organizar el número de puntos a usar de tal modo que sea
un potencia de dos. Además no se evaluarán directamente los coeficientes 8ai < y 8bi < de
la fórmula anterior, sino que se tendrá que calcular los coeficientes complejos 8ci <. La
expresión de estos coeficientes complejos se deduce tomando la expresión compleja
ai - Â bi , cuyo valor es:
ai - Â bi =
1
m-1
A⁄2j=0
m
y j cosHi x j L - Â y j senHi x j LE,
Hi = 0, 1, 2, ..., mL.
Aplicando la fórmula de Euler se obtiene:
ai - Â bi =
1
m
m-1
y j e-Â i x j ,
⁄2j=0
Hi = 0, 1, 2, ..., mL.
Como los puntos donde se interpola son @-p, pD y tienen por abscisas a
41
Proyecto Fin de Carrera
x j = -p +
jp
m
para j = 0, 1, ..., 2 m - 1, entonces:
-Â i J-p+
jp
N
ai - Â bi =
1
m
m-1
yj e
⁄2j=0
ai - Â bi =
1
m
m-1
y j e- 2 p i jêH2 mL e p i
⁄2j=0
ai - Â bi =
1
m
m
,
m-1
H-1Li ⁄2j=0
y j e-Â 2 p i jêH2 mL
Hi = 0, 1, 2, ..., mL.
Tomando el valor del coeficiente complejo ci como el valor del sumatorio, por
lo que la relación entre los coeficientes 8ai < y 8bi < del polinomio y 8ci < viene dada por:
ai - Â bi =
1
m
H-1Li ci ,
m-1
ci = ⁄2j=0
y j e-Â 2 p i jêH2 mL
m-1
ci = ⁄2j=0
y j W2 m
-i j
ô
Hi = 0, 1, 2, ..., mL.
Como conclusión se establece que, los coeficientes complejos 8ci < se corresponden con las componentes de la transformada discreta de Fourier c = b = DFT HyL:
m-1
ci = bi = ⁄2j=0
y j W2 m
-i j
Hi = 0, 1, 2, ..., 2 m - 1L.
m-1
Por tanto, teniendo el conjunto de = 2 m = 2 p puntos 8xi , yi <2i=0
que dividen
uniformemente el intervalo cerrado @-p, pD, siendo las abscisas xi
xi = -p +
ip
m
i = 0, 1, ..., 2 m - 1,
y sus ordenadas yi = f Hxi L. Si b = c = DFT HyL es la transformada discreta de Fourier del
vector y, entonces el polinomio trigonométrico interpolador de grado m - ésimo que
satisface Sm Hxi L = yi para i = 0, 1, 2, ..., 2 m - 1 tiene la expresión:
Sm HxL =
a0
2
+
am cosHm xL
2
+ ⁄m-1
i=1 Hai cosHi xL + bi senHi xLL
42
Software de Aplicación de la FFT
siendo las constantes 8ai < y 8bi < de Sm HxL:
ai - Â bi =
a0 =
b0
,
m
H-1Li
m
bi ,
am =
ai = H-1Li
ReH bi L
m
bi = H-1Li
-ImHbi L
m
bm
m
=
e-Â p i
m
ReHbi L,
= - e m ImH bi L ,
-Â p i
Hi = 1, 2, ..., m - 1L.
Descripción de cálculo de los coeficientes del polinomio trigonométrico
en [0 2p]
La transformada discreta de Fourier b = DFT HyL depende de las ordenadas yi , por
lo que su valor para un vector y no dependerá de las abscisas xi . Por tanto, si se tiene una
función f HxL definida en el intervalo @-p, pD y se quiere saber el polinomio trigonométrico
que interpola los puntos 8xi , yi <i=0
pero para los mismos puntos equistantes en el intervalo
@0, 2 pD con las mismas ordenadas yi , se debe realizar un cambio de intervalo de @-p, pD a
@0, 2 pD. La nueva función gHzL definida sobre éste nuevo intervalo se obtiene con el cambio
de variable x = z - p:
x œ @-p, pD,
z œ @0, 2 pD,
z= x+p
fl
x = z-p
f HxL
fl
gHzL = f Hz - pL
(12)
Cambiando de variable para definir el polinomio trigonométrico interpolador en
@0, 2 pD se tiene la expresión de Sm HzL:
43
Proyecto Fin de Carrera
a0
Sm HzL =
2
+
am cosHm Hz - pLL
2
m-1
+ ‚ Hai cosHi Hz - pLL + bi senHi Hz - pLLL,
(13)
i=1
y empleando las fórmulas trigonométricas:
ai cosHi Hz - pLL =
ai 8cosHi zL cosH-i pL + senHi zL senH-i pL < = H-1Li ai cosHi zL
bi senHi Hz - pLL =
(14)
bi 8senHi zL cosH-i pL - cosHi zL senH-i pL < = H-1Li bi senHi zL
se reescribe el polinomio trigonométrico:
a0
Sm HzL =
2
+ H-1L
a0 =
b0
m
,
ai = H-1Li
bi = H-1Li
m
am cosHm zL
2
am =
m-1
+ H-1L ‚ Hai cosHi zL + bi senHi zLL
i
i=1
bm
ReH bi L
m
(15)
m
-ImH bi L
Hi = 1, 2, , ..., m - 1L.
m
m-1
Luego, dado el conjunto de = 2 m puntos 8xi , yi <2i=0
que dividen uniformemente
el intervalo cerrado @0, 2 pD, siendo las abscisas xi
xi =
ip
m
i = 0, 1, ..., 2 m - 1,
y sus ordenadas yi = f Hxi L. Y sea b = DFT HyL la transformada discreta de Fourier del
vector y. El polinomio trigonométrico interpolador de grado m - ésimo que satisface
Sm Hxi L = yi para i = 0, 1, 2, ..., 2 m - 1 tiene la expresión:
Sm HxL =
a0
2
+
am cosHm xL
2
+ ⁄m-1
i=1 Hai cosHi xL + bi senHi xLL
siendo las constantes 8ai < y 8bi < de Sm HxL
a0 =
b0
,
m
am =
bm
m
44
Software de Aplicación de la FFT
ai =
ReHbi L
,
m
bi =
-ImH bi L
,
m
Hi = 1, 2, ..., m - 1L.
è Algoritmo 4. Polinomio trigonométrico interpolador en [-p, p]
y [0, 2p] usando la FFT con el teorema de duplicación
Polinomio trigonométrico interpolador en
[ -p
p, p ] y [ 0, p ] usando la FFT
H* Los argumentos que recibe la función son y ,
que es la función a interpolar y0 es un parametro para saber si la función
a interpolar esta es forma de vector o en forma de función N es el
número de puntos y por último int que es el intervalo . Se devolverá
una variable S que sera el polinomio interpolado en ese intervalo *L
Input HHyL, HY0 L, HN L, HintLL
H* Cálculos previos *L
M ≠ N ê2
P ≠ Log2H2 * M L
H* Intervalo @ -p, p D *L
If int <> @0, 2 pD
(* Cálculo de xi*)
For i = 1, 2, 3, ..., N do
Xi ,1 ≠ intH1L + HHi - 1L * intH2LL ê M
End
(* Cálculo de yi*)
If Y0 ã 0
For l = 1, 2, 3, ..., N do
Yl ,1 ≠ sustituir H y ,Xl ,1 M
45
Proyecto Fin de Carrera
End
Else
For j = 1, 2, 3, ..., N do
Yl ,1 ≠ yH jL
End
End
(* Cálculo de Beta*)
Beta ≠ fft HYL
(* Primer elemento del vector "a" del polinomio de
interpolacion*)
a 1 ≠ BetaH1L ê M
(* Último elemento del vector "a" del polinomio de
interpolacion*)
a M +1 ≠ Beta(M+1) / M
(* Cálculo del resto del vector "a" y el vector "b"*)
For t = 2, 3, ..., M do
a t ≠ parte_real HH-e H p * t L * i L ê ML * parte_realHBetaHtLL
bt ≠ - parte_real HH-e H p * t L * i L ê ML *
parte_imaginariaHBetaHtLL
End
For p = 2, 3, ..., M do
Z p ≠ a p * cosHHp-1L*xL + bt * sinHHp-1L*xL
End
(* S m es la función de interpolación*)
S m ≠ Ha 1 ê 2 L + Ha M +1 * cosHM* xL ê2 L + ⁄M
j=2 Z j L
Else
46
Software de Aplicación de la FFT
(* Intervalo @0, 2 pD*)
(* Cálculo de xi*)
For i = 1, 2, 3, ..., N do
Xi ,1 ≠ HHi - 1L * pL ê M
End
(* Cálculo de yi*)
If Y0 ã 0
For l = 1, 2, 3, ..., N do
Yl ,1 ≠ sustituir H y ,Xl ,1 M
End
Else
For j = 1, 2, 3, ..., N do
Yl ,1 ≠ yH jL
End
End
(* Cálculo de Beta*)
Beta ≠ fft HYL
(* Primer elemento del vector "a" del polinomio de
interpolacion*)
a 1 ≠ BetaH1L ê M
(* Último elemento del vector "a" del polinomio de
interpolacion*)
a M +1 ≠ Beta(M+1) / M
(* Cálculo del resto del vector "a" y el vector "b"*)
For t = 2, 3, ..., M do
a t ≠ parte_real HBetaHtL ) / M
47
Proyecto Fin de Carrera
bt ≠ - parte_imaginaria HBetaHtL ê ML
End
For p = 2, 3, ..., M do
Z p ≠ a p * cosHHp-1L*xL + bt * sinHHp-1L*xL
End
(* S m es la función de interpolación*)
S m ≠ Ha 1 ê 2 L + Ha M +1 * cosHM* xL ê2 L + ⁄M
j=2 Z j L
End
Return HS L
Output
à Ejemplo
3. Sea f HxL = xHp - xL definida en @-p, pD. Determinar el polinomio
trigonométrico interpolante S4 HxL que aproxima a f HxL, aplicando la transformada rápida
de Fourier HFFT L . Se tomarán = 2 m = 2 p = 8 puntos con m = 4 y p = 3. Representar
las funciones f HxL y S4 HxL.
à Solución
y = ' HHxL ∗ Hpi − HxLLL ';
% En forma de función
y0 = 0;
int = @−pi; piD;
n = 8;
x=
−3.1416
−2.3562
−1.5708
−0.7854
0
0.7854
1.5708
2.3562
y = −19.7392
−12.9539
−7.4022
48
Software de Aplicación de la FFT
−3.0843
0
1.8506
2.4674
1.8506
beta =
−37.0110
−26.7181 + 23.8273 i
−14.8044 + 9.8696 i
−12.7603 + 4.0881 i
−12.3370
−12.7603 − 4.0881 i
−14.8044 − 9.8696 i
−26.7181 − 23.8273 i
a = −9.2528
6.6795
b=0
− 2.4674
5.9568
− 3.7011
1.0220
% Resultado final Sm
49
3.1901
− 3.0843
Proyecto Fin de Carrera
Gráfica de f (x) = x*(pi-x) y de p (x)
10
f (x) = x*(pi-x)
p (x)
5
0
Y
-5
-10
-15
-20
-25
-4
-3
-2
-1
0
X
1
2
3
4
Gráficas de f HxL = x * Hp - xL y pHxL = S4 HxL
Figura 1
à Ejemplo
3. Sea f HxL = 3 ê H5 - 4 * cos HxLL definida en @-p, pD. Determinar el
polinomio trigonométrico interpolante S4 HxL que aproxima a f HxL, aplicando la
transformada rápida de Fourier HFFT L . Se tomarán = 2 m = 2 p = 8 puntos con m = 4
y p = 3. Representar las funciones f HxL y S4 HxL.
à Solución
y = ' 3. ê H5 − 4. ∗ cos HxLL ';
y0 = 0;
int = @−pi; piD;
n = 8;
x = −3.1416
−2.3562
−1.5708
−0.7854
0
0.7854
1.5708
2.3562
y = 0.3333
0.3832
0.6000
1.3815
3.0000
50
Software de Aplicación de la FFT
1.3815
0.6000
0.3832
beta = 8.0627
−4.0784
2.1333
−1.2549
1.0039
−1.2549
2.1333
−4.0784
a = 2.0157 1.0196 0.5333 0.3137 0.2510
b=0 0 0 0
% Resultado final Sm
Gráfica de f (x) = 3/(5-4*cos (x)) y de p (x)
3
f (x) = 3/(5-4*cos (x))
p (x)
2.5
Y
2
1.5
1
0.5
0
-4
-3
-2
-1
0
X
1
2
3
Gráficas de f HxL = 3 ê H5 - 4 * cos HxLL y pHxL = S4 HxL
Figura 2
51
4
Proyecto Fin de Carrera
8. Aproximación de Chebyshev
8.1 Polinomios de Chebyshev y nodos de
Chebyshev
1. Relación de recurrencia
Los polinomios de Chebyshev se generan a partir de la relación de recurrencia
siguiente:
T0 HxL = 1
T1 HxL = x
T2 HxL = 2 x2 - 1
T3 HxL = 4 x3 - 3 x
... ... ..
Tk HxL = 2 x Tk-1 HxL - Tk-2 HxL
(16)
Hk > 2L.
2. Representación trigonométrica en @-1, 1D
El polinomio de Chebyschev verifica:
Tn HxL = cosHn arccosHxLL
H-1 § x § 1L.
(17)
3. Ceros simples en @-1, 1D y en el intervalo [a, b]
El polinomio Tn HxL tiene n ceros distintos, los puntos xi , que se encuentran todos en
el intervalo @-1, 1D, llamándose a estos ceros nodos o abscisas de Chebychev. El valor de
estos nodos es
xi = cos
H2 i + 1L p
2n
H0 § i § n - 1L.
52
(18)
Software de Aplicación de la FFT
Pero también se puede considerar los polinomios de Chebyshev definidos en un
intervalo cerrado general @a, bD, para lo cual los nodos de interpolación de Chebyshev se
calculan realizando el cambio de variable siguiente:
x=
b-a
2
x œ @-1, 1D,
z+
a +b
H0 § i § n - 1L
2
z œ @a, bD
(19)
que transforma los números xi del intervalo @-1, 1D en el correspondientes número zi del
intervalo @a, bD. Por tanto, los nodos o abscisas de Chebyshev correspondientes a
Tn HxL ª Tn HzL, definido en @a, bD son:
xi =
b-a
2
cos
H2 i + 1L p
2n
+
a +b
2
H0 § i § n - 1L
(20)
4. La extrema de Chebyshev
Los polinomios Tn HxL = cosHn arccosHxLL tienen la propiedad tal que 1 § Tn HxL § 1.
Además, Tn HxL toma los extremos + 1, esto es que, Tn Hx r L = ≤1 en:
xr = cos qr = cosK
rp
O
Hr = 0, 1, ... .... L.
(21)
porque Tn Hx r L= cos qr = cos r p = ≤ 1.
8.2 Aproximación de Chebyshev
El polinomio de aproximación de Chebyshev pn HxL de grado menor o igual a n para
una función f HxL definida en @-1, 1D se puede escribir como la suma ponderada de los
polinomio de Chebyshev 8Tk HxL<:
f HxL º pn HxL = ⁄nk=0 ck Tk HxL
en la que los coeficientes 8ck < se calculan de la siguiente manera:
53
Proyecto Fin de Carrera
ck = IDCT H f HxLL
H0 § k § nL.
(22)
donde IDCT es la Transformada discreta del coseno inversa de la función f HxL, pudiéndose
calcular la IDCT como
2
DCT. Se verá ahora cómo se relacionan la FFT con la DCT, ya
que el objetivo es calcular la aproximación rápida de Chebyshev con la trasformada rápida
de Fourier.
ô Relación entre la FFT y DCT
Sea la DFT la trasformada discreta de Fourier de longitud 2 usándose el
vector x que se utilizaría para la DCT de longitud + 1, x = Ax0, x1, ..., xn E, entonces:
2 -1
Xr = ⁄
l=0
-
donde w2 = ‰
2 jp
2
rl
xl w
2
Hr = 0, 1, 2, ..., 2 - 1L
= cosI p M - j senI p M, y xn+1, xn+2, , ..., x2 n-1 son los elementos
añadidos al vector original x, simétricos a xn ,
x2 -l ª xl
Hl = 0, 1, 2, ..., L.
Se obtiene la DCT de longitud + 1 enbebida dentro de la FFT de longitud 2 como se verá a continuación.
54
Software de Aplicación de la FFT
2 -1
Xr = ⁄
2
l=0
-1
= ⁄ xl w
rl
l=0
2
-1
rl
= ⁄ xl w
ô
Hr = 0, 1, 2, ..., 2 - 1L
rl
xl w
l=0
2
-1
rl
= ⁄ xl w
l=0
2
-1
rl
l=0
2
= ⁄ xl w
-1
2 -1
+ ⁄
2
l=
r H2 -lL
+⁄
x
l=1 2 -l
rH2 L
+
w
2
w
2
-r l
l=1
2
-r l
l=1
2
-r l
=2
-1
rl
l=1
2
2
-1
+ ⁄ xl cosI
l=1
+ x
2
l=1
= x0 + H-1L x + ⁄ xl H w
r
= 1
2
-1
2
r
2
‹ w
+ ⁄ xl w
rl
x0 + H-1L x H ‹ x2 -l = xl L
⁄ x w
+ ⁄ xl w
= x0 + ⁄ xl w
l=0
rl
xl w
prl
2
-r l
+ w
2
L
-r w
2
2
‹ w
= -1
2
M
= 2 Cr HDonde Cr y Xr son valores realesL
Con esto, si @C0 , C1 , ..., C D = DCTIAx0, x1, ..., xn EM son los resultados deseados
de la Traformada discreta del coseno y @X0 , X1 , ..., X D = DFTIAx0, x1, ..., xn EM, siendo
estos los resultados de la traformada discreta de Fourier entonces:
@C0 , C1 ... .. C D =
1
2
@X0 , X1 ... .. X D.
55
Proyecto Fin de Carrera
Como conclusión la tarea para programar la DCT de longitud + 1 se puede
llevar a cabo programando la DFT de longitud 2 pudiendo ser implementada con un
algoritmo FFT O H log L.
è Algoritmo 5. Polinomios de Chebyshev
Polinomio de Chebyshev de grado N
H* Los argumentos que recibe la función son n ,
que es el grado del polinomio de Chebyshev que se desea construir,
como resultado se obtendrá el polinomio de grado n *L
Input HHnLL
H* Inicializaciones *L
t0 ≠ 1
t1 ≠ [1 0]
H* Se calculan los coeficientes del polinomio. *L
if n ã 0
T ≠ t0
else if Hn ã 1L
T ≠ t1
else
For k = 2, 3, ..., n do
T ≠ @2* t1 0D - @0 0 t0 D
t0 ≠ t1
t1 ≠ T
End
End
56
Software de Aplicación de la FFT
H* Con los coeficientes se construye el polinomio. *L
For i = 1, 2, ..., n + 1 do
FHi,1L ≠ TH1,i L * y HHn+1L-iL
End
(* Sumatorio del vector para tener el polinomio completo. *)
F ≠ ⁄n+1
i=1 FHi,1L
Return HF L
Output
è Algoritmo 6. Algoritmo de la Transformada discreta del
coseno DCT con la función de la Transformada rápida de Fourier
Algoritmo de la DCT con FFT
H* Los argumentos que recibe la función son x que es el
vector al que se le va a aplicar la Trasformada Discreta del
coseno por medio del algoritmo de la FFT que posee MATLAB,
como resultado se obtendrá la DCT del vector*L
Input HHxLL
H* Se calcula la longitud del vector *L
N ≠ longitudHxL
H* Paso del vector de N a 2N. *L
For i = 1, 2, ..., N do
rHi,1L ≠ xHN -i + 1, 1L
End
For i = N + 1, N + 2, ..., 2 N do
57
Proyecto Fin de Carrera
rHi,1L ≠ xHi- N , 1L
End
(* Traspuesta del vector. *)
r ≠ r'
(* Se llama al algoritmo de la FFT. *)
C ≠ fftHrL
(* Se pasa FFT a DCT. *)
For i = 0, 1, ..., 2 * N - 1 do
cambioHiL ≠e H- j * 2 * p * HN -0.5L * i ê H2*N L L
End
For j = 0, 1, ..., 2 * N - 1 do
f H jL ≠ real(CH jL /cambioH jL )
End
For k = 1, 2, ..., N do
DHkL ≠ f HkL /,(2*N)
End
DH1L ≠ DH1L /,2
Return HDL
Output
è Algoritmo 7. Algotitmo de aproximación rápida de Chebyshev
en intervalo [ -1, 1 ]
Algoritmo Aproximación rápida de Chebyshev
58
Software de Aplicación de la FFT
H* Los argumentos que recibe la función son int que es el
intervalo de la interpolación, N que será el número de puntos
y por último f es la función continua que se va a interpolar,
el resultado del módulo es la función aproximada por Chebyshev *L
Input HHint, N , f LL
H* Declaración de la variable simbólica *L
y ≠ symsH' y 'L
H* Se comprueba que el intervalo es H-1;1L. *L
if Hint ã H-1; 1LL
H* Se calculan los nodos de Chebyshev. *L
if HN ã 1L
nodos ≠ @0D
else
For i = 0, 1, ..., N +1do
nodosH1,iL ≠ cosHH2*i+1L* pL ê HH2*NL+2L
End
H* Evaluación en los nodos de la función a interpolar. *L
For j = 1, 2, ..., N do
ZH j,1L ≠ f I nodosH1, jL M
End
End
else
H* Cálculo los nodos de Chebyshev. *L
if HN ã 1L
nodos ≠ @0D
59
Proyecto Fin de Carrera
else
For i = 0, 1, ..., N +1 do
nodosH1,iL ≠ HHintH2L - intH1L L ê 2L * cosHH2 * i + 1L * pL ê H2 * N L L
+ HHintH1L - intH2L L ê 2L
End
H* Evaluación en los nodos de la función a interpolar. *L
For j = 1, 2, ..., N do
ZH j,1L ≠ f I nodosH1, jL M
End
End
End
H* Se llama a la función de la DCT . *L
C ≠ H2 ê HN + 1L L * DCT_
_con_
_FFTHZL
H* Se calcula el polinomio de Chebyshev . *L
For i = 1, 2, ..., N + 1 do
T ≠Polinomio_De_Chebyshev_grado_n(i-1)
RHi,1L ≠ CHiL * T
End
(*Sumatorio del vector para tener el polinomio completo. *)
R ≠ ⁄n+1
i=1 RHi,1L
Return HRL
Output
60
Software de Aplicación de la FFT
Ejemplo 4. Sea la función f HxL = e-x .
a)
Calcular los polinomios de Chebyshev p2 HxL y p3 HxL que aproximan la función en
el intervalo @-1, 1D .
b)
Dibujar las funciones f HxL y el polinomio pHxL que lo aproxima.
à Solución
f = exp H−xL;
int = @−1; 1D;
N = 3;
% Nodos de Chebyshev
0.9239 0.3827 − 0.3827 − 0.9239
% Sustitución de los nodos en la función f
z = 0.3970
0.6820
1.4662
2.5190
% Coeficientes de Chebyshev
c = 1.2661 − 0.799 0.1919 − 0.0310
% Polinomios de Chebyshev
1
y
2 ∗ y^2 − 1
4 ∗ y^3 − 3 ∗ y
% Aproximación y resultado final
61
Proyecto Fin de Carrera
Gráfica de f (x) = exp (-x) y de p (x)
25
f (x) = exp (-x)
p (x)
20
Y
15
10
5
0
-5
-4
-3
-2
-1
0
X
1
2
3
4
Gráficas de f HxL = e-x y pHxL.
Figura 3
à Ejemplo 5.
Sea la función f HxL =
1
.
Ix2 +1M
a)
Calcular los polinomios de Chebyshev p2 HxL y p3 HxL que aproximan la función en
el intervalo @-1, 1D .
b)
Dibujar las funciones f HxL y el polinomio pHxL que lo aproxima.
à Solución
f = 1 ê HHx ^ 2L + 1L;
int = @−1; 1D;
N = 3;
% Nodos de Chebyshev
0.9239 0.3827 − 0.3827 − 0.9239
% Sustitución de los nodos en la función f
z = 0.5395
0.8723
0.8723
0.5395
% Coeficientes de Chebyshev
c = 0.7059 0 − 0.1664 0
62
Software de Aplicación de la FFT
% Polinomios de Chebyshev
1
y
2 ∗ y^2 − 1
4 ∗ y^3 − 3 ∗ y
% Aproximación y resultado final
Gráfica de f(x) = 1/(x 2+1) y de p(x)
1
f(x) = 1/(x 2+1)
p(x)
0.95
0.9
0.85
Y
0.8
0.75
0.7
0.65
0.6
0.55
0.5
-1
-0.8
-0.6
-0.4
-0.2
Gráficas de f HxL =
0
X
1
Ix2 + 1M
Figura 4
63
0.2
0.4
y pHxL.
0.6
0.8
1
Proyecto Fin de Carrera
9. Estudio de arquitectura
A continuación se estudiarán las alternativas propuestas para la implantación de
proyecto. De cada alternativa se propondrán tanto los elementos Software con Hardware
que mejor convendrían para la realización de la aplicación, haciendo seguidamente un
estudio contemplando diferentes ámbitos y sacando unas conclusiones, eligiéndose al final
la mejor propuesta.
Los componente software que se proponen a continuación son los básicos para
desarrollar cualquier aplicación matemática. En primer lugar un sistema operativo
comercial, después un procesador de textos, luego una herramienta matemática con la que
se pude programar y hacer cálculos y por último un software que permita general ficheros
PDF en los que se pueda presentar la documentación.
En cuanto a los componentes hardware las dos alternativas propuestas son
prácticamente la mismo ya que solo hace falta un ordenador para el desarrollo y ejecución
de la aplicación ya sea de sobremesa o sea un ordenador portátil.
Una vez se seleccione la alternativa se establecerá una planificación temporal del
proyecto, viéndose cada una de las etapas que se han comentado antes en la metodología,
viendo de forma aproximada el reparto de tiempo en cada una de las fases.
64
Software de Aplicación de la FFT
9.1 Especificación de alternativa-1
à TÍTULO / CÓDIGO
Aplicación Software FFT con Mathematica (FFT01)
Área
Matemáticas y Métodos Numéricos.
Antecedentes
Se sabe de la implantación de otros sistema y aplicaciones matemáticas construidas
con esta herramienta Mathematica obteniendo muy buenos resultados, además es una de las
más importantes el sector, siendo una alternativa fiable y probada por muchos usuarios.
Además es una de las mejores aplicaciones que trabaja con variables simbólicas y cálculo
simbólico y muy fiable ejecutándose bajo Windows.
Requisitos
Se necesita de un ordenador capaz de soportar una gran cantidad de operaciones con
cálculos muy pesados ya que se utilizarán variables de gran magnitud y complejidad.
Además la GUI se debe programar en Java 2 SE, y se conoce la compatibilidad de las dos
herramientas. Tanto Mathematica como Java se pueden integrar sin ningún problema, por
eso es necesario que el sistema donde vaya a funcionar y ejecutar tenga la aplicación JDK
(Java Development Kit). Por último, comentar que la documentación se haría en Microsoft
Office, herramienta líder en el sector y que tendrá que estar instalada en el sistema.
Necesidades Software
æ Sistema Operativo Windows XP SP2 Home Edition.
65
Proyecto Fin de Carrera
æ Software Ofimático Microsoft Office Vista Proffesional Edition.
æ Software Matemático Mathematica 6.0.
æ JDK Java 2 SE con etbeans 6.1.
æ Adobe Acrobat 8 Proffesional.
Necesidades Hardware
æ Ordenador personal con procesador Intel Pentium IV 1,8 GHz, con 1 GB de memoria
RAM, disco duro de 80 GB , tarjeta gráfica de 128 MB y unidad lectora de CD-DVD.
9.2 Especificación de alternativa-2
à TÍTULO / CÓDIGO
Aplicación Software FFT con Matlab (FFT02)
Área
Matemáticas y Métodos Numéricos.
Antecedentes
66
Software de Aplicación de la FFT
La herramienta matemática Matlab es una de las más importantes en el sector,
usada por usuarios que necesitan no solo potencia y rapidez en el cálculo, sino hacer
módulos y aplicaciones informáticas de manera sencilla. Gracias a su cómoda interfaz
GUIDE se pueden construir interfaces de usuario con la misma herramienta sin tener que
utilizar otro sistema. Además es compatible con todos los lenguajes de programación,
pudiendo trasportar la aplicación a cualquier otro sistema. También se conoce que se usa en
el campo de los métodos numéricos y de telecomunicaciones.
Requisitos
Se necesita un ordenador capaz de soportar una gran cantidad de operaciones con
cálculos muy pesados ya que se utilizarán variables de gran magnitud y complejidad. La
documentación se hará en la herramienta Mathematica ya que se necesitan escribir multitud
de fórmulas y teorías matemáticas, siendo de fácil manejo. También cuenta con opciones de
procesador de textos cómoda y sencilla, pudiéndose redactar la documentación y poderla
maquetar de forma elegante. Por último, el sistema deberá tener instalado Windows Vista,
aunque es un sistema operativo nuevo en el mercado es totalmente compatible y funciona
perfectamente tanto con Matlab como con Mathematica.
Necesidades Software
æ Sistema Operativo Windows Vista Home Edition.
æ Software Matemático Matlab 7.0.
67
Proyecto Fin de Carrera
Software Matemático Mathematica 6.0.
æ PDF Creator.
Necesidades Hardware
æ Ordenador personal con procesador Intel Core 2 Duo 2,33 GHz, con 2 GB de memoria
RAM, disco duro de 80 GB, tarjeta gráfica de 128 MB y unidad lectora de CD-DVD.
9.3 Valoración de alternativas
Para saber cuál de las dos alternativas se elegirá se crearán tres matrices de
evaluación, que se expondrán a continuación. Cada una tratará sobre tres aspectos de
interés, evaluación operativa, técnica y económica.
La matriz tendrá una serie de diferentes aspectos o características dependiendo de la
organización, del negocio al que se dedica y del sistema en estudio, asignando a cada uno
un peso que oscilaran entre los valores 1 y 3, siendo 1 el peso menor y por lo tanto teniendo
la valoración más baja, o teniendo un 3 que será el que tendrá mayor relevancia dentro de la
aplicación.
Seguidamente se valorarán los parámetros tratados en cada una de las alternativas
según el grado de cumplimiento que la alternativa tiene de ese parámetro dando una
puntuación. Estos valores oscilan entre el 1 y el 3, siendo el 1 el valor que se refiere al poco
cumplimiento del parámetro y el 3 correspondiendo a un cumplimiento perfecto.
68
Software de Aplicación de la FFT
Por último, para obtener la puntuación total de la alternativa se multiplicará cada
parámetro el peso con su puntuación obtenida teniendo su valor total. Seguidamente se
sumarán todos los valores totales de cada uno de los parámetros teniendo el resultado final
de cada alternativa. La que tenga valor más alto será a que tenga mejor valoración y por lo
tanto la que se aplique al proyecto.
9.3.1 Matriz de evaluación operativa
1
ALTER@ATIVAS
Parámetros ê Peso
Puntuación
2
Valor
Puntuación
Valor
Fiabilidad de los datos H3L
3
9
3
9
Facilidad de uso y manejo
2
6
3
9
Control de sistema H2L
2
4
2
4
Agilidad de la aplicación H3L
2
6
3
9
Seguridad H1L
1
1
2
2
aplicación H3L
TOTAL
26
69
33
Proyecto Fin de Carrera
9.3.2 Matriz de evaluación técnica
1
ALTER@ATIVAS
Parámetros ê Peso
Puntuación
2
Valor
Puntuación
Valor
Requisitos Software H3L
3
9
3
9
Requisitos Hadware H3L
2
6
3
9
Portabilidad software H3L
2
4
2
4
Compatibilidad con
otros lenguajes H2L
2
4
3
6
Manejo de caracteres
simbólicos H3L
3
9
2
6
3
6
3
6
2
2
2
2
1
3
3
9
2
6
3
9
Potencia de calculo H2L
Mantenibilidad del
sistema H1L
Biblioteca con FFT H3L
Opciones de creación
GUI H3L
TOTAL
49
70
60
Software de Aplicación de la FFT
9.3.3 Matriz de evaluación económica
Costes de implantación
ALTER@ATIVAS
Parámetros ê Peso
Puntuación
1
Valor
Puntuación
2
Valor
Coste de
desarrollo H3L
3
9
3
9
Costes de puesta
en marcha H2L
2
6
2
6
2
4
2
4
Coste de formación H1L
Costes de tecnología
Coste Hardware H2L
2
4
3
6
Coste Software H3L
1
3
3
9
Costes operacionales
Costes de mantenimiento
y mejora H1L
TOTAL
2
2
28
71
2
2
36
Proyecto Fin de Carrera
9.3.4 Valoración final de cada alternativa
Parámetros
Alternativa 1 Alternativa 2
Parámetros Operativos
26
33
Parámetros Técnicos
49
60
Parámetros económicos
28
36
TOTAL
103
129
9.4 Elección de alternativa
Como se puede ver las dos opciones son igual de válidas, pero la que se va a optar
es la Alternativa 2, ya que posee mayor puntuación. Para aclarar la elección se explicarán a
continuación las razones, por las que se ha elegido la segunda alternativa que son las por
las que se han dado las puntaciones más altas.
En primer lugar se optará por un sistema operativo Windows Vista, en un ordenador
con procesador Intel Core 2 Dúo 2,33 GHz, con 2 GB de memoria RAM, ya que se
necesitará mucha potencia para procesar los cálculos. No vale cualquier procesador, de
hecho el programa MATLAB, no se instala en ordenadores con poca potencia, y en general
también se necesita bastante memoria RAM teniendo más que suficiente con 1 ó 2 GB.
En relación con la elección de la aplicación matemática entre MATLAB y
Mathematica, decir que prácticamente son iguales estas dos herramientas. La diferencia
fundamental por la que se ha elegido la primera, es por un lado el poder operarar con variables y
operaciones simbólicas, pero lo fundamental es que posee una biblioteca de funciones FFTW con
el algoritmo de la FFT. Por otro lado, MATLAB tiene bibliotecas para poder diseñar interfaces de
72
Software de Aplicación de la FFT
usuario, con GUIDE, que permite integrar fácilmente los módulos y la propia interfaz GUI, sin
tener que utilizar Java y con esto tener que instalar más aplicaciones extras como la JDK. Por
último se ha elegido MATLAB por su potencia y calidad de representación de funciones gráficas.
Para finalizar comentar la elección del procesador de textos. A pesar de que
Windows Office es la mejor herramienta ofimática en general, se usará la aplicación
matemática Mathematica en lugar del conocido procesador de texto, ya que este paquete
matemático dispone de un procesador de textos con notación matemática que permite
pueden escribir de forma sencilla, tanto fórmulas como cualquier símbolo, e integra el
texto, las ecuaciones matemáticas y los gráficos de un modo profesional. Con el procesador
de Office sería una tarea pesada y ardua.
9.5 Planificación temporal del proyecto
El siguiente diagrama de Gantt refleja cómo se ha repartido el tiempo a lo largo del
proyecto. Se han tenido en cuenta tanto los exámenes intercuatrimestrales de los días 19 al
23 de Noviembre y los segundos intercuatrimestrales del 21 al 25 de Abril, así como los
exámenes de Febrero. Esto conlleva a que los días anteriores a esos periodos de exámenes
tampoco se realizó ninguna actividad del proyecto. Se tendrá también en cuenta que cada
día se han dedicado 4 horas, como media durante todo el año.
73
Proyecto Fin de Carrera
Octubre 2007
D
L
M
X
J
V
S
1
2
3
4
5
6
7
8
9
10
11
12
13
4
5
6
14
15
16
17
18
19
20
11
12
13
27
18
19
20
25
26
27
21
22
23
24
28
29
30
31
Diciembre 2007
D
L
M
X
J
V
2
3
4
5
6
7
9
10
11
12
13
16
17
18
19
23
30
24
31
25
26
S
M
X
26
L
J
V
X
V
S
1
J
2
3
7
8
9
10
14
15
16
17
21
22
23
24
28
29
30
Febrero 2008
L
M
1
2
3
4
5
1
2
8
6
7
8
9
10
11
12
3
4
5
6
7
8
9
14
15
13
14
15
16
17
18
19
10
11
12
13
14
15
16
20
21
22
20
21
22
23
24
25
26
17
18
19
20
21
22
23
27
28
29
27
28
29
30
31
24
25
26
27
28
29
J
X
M
D
Marzo 2008
L
25
D
Enero 2008
1
D
Noviembre 2007
S
D
L
Abril 2008
V
S
D
L
1
M
J
X
M
X
J
V
S
Mayo 2008
V
S
D
L
M
J
X
V
S
1
2
3
1
2
3
4
5
2
3
4
5
6
7
8
6
7
8
9
10
11
12
4
5
6
7
8
9
10
9
10
11
12
13
14
15
13
14
15
16
17
18
19
11
12
13
14
15
16
17
16
17
18
19
20
21
22
20
21
22
23
24
25
26
18
19
20
21
22
23
24
23
30
24
31
25
26
27
28
29
27
28
29
30
25
26
27
28
29
30
31
MEMORIA
DESCRIPTIVA
ANÁLISIS DE
REQUISITOS
PROGRAMACIÓN
Y PRUEBAS
RECOGIDA Y
ANALISIS
MÓDULOS
VALORACIÓN
EACONÓMICA
IDENTIFICACIÓN
DE NECESIDADES
DISEÑO
ARQUITECTURA
Planificación temporal del proyecto.
Figura 5
74
CONCLUSIONES
Software de Aplicación de la FFT
10. Diseño externo
Se describirá el diseño de cada uno de las ventanas que se han desarrollado para la
aplicación dando una pequeña descripción y poniendo una captura de cada una de ellas.
Como características principales indicar que se estudió en primer lugar al usuario que
utilizará la aplicación, que serán no solo matemáticos sino cualquier ingeniero, por eso
todas las ventanas tienen que tener un lenguaje matemático comprensible para este tipo de
usuarios. Además el usuario quiere que la disposición de todos los iconos y elementos de
las ventanas sean visibles y accesibles, pero no molestos, pudiendo hacer las operaciones
con las menos interacciones posibles, y no acumulando en la pantalla objetos que serían
molestos y desorientarían al usuario.
Se disponen de un total de cinco ventanas principales, que son los pilares de la
aplicación, que corresponderán a los módulos programados. Luego se programarán
ventanas auxiliares que serán complementarias a éstas.
10.1 Diseño de ventanas
1. Diseño de ventana principal
à NOMBRE
Ventana de menú de la aplicación.
Código
75
Proyecto Fin de Carrera
Menu_PFC.
Ventanas a las que llama
-Ventana de Información (Info_0).
-Ventana de Multiplicación de números esteros de gran magnitud (Módulo_1).
-Ventana de Multiplicación de polinomios de cualquier grado (Módulo_2).
-Ventana de Aproximación rápida de Chebyshev (Módulo_4).
-Ventana de Aproximación Trigonométrica (Módulo_3).
-Ventana de Salida (modaldlg).
Descripción
La ventana del menú es la principal de la aplicación. Posee un menú en la parte
superior con el nombre de los diferentes módulos para poder acceder a cada uno de ellos,
además de la opción de salida de la aplicación. En esta ventana se pondrá el nombre de la
aplicación, también se pondrá el nombre del autor y del director del proyecto. Se colocará
en la parte inferior de la ventana un botón de información para que el usuario acceda y se
informe de las diferentes acciones que puede efectuar en el programa. Por último y para
rellenar se programará una función toroide en tres dimensiones de llamativos colores que se
dispondrá en medio de la ventana para hacerla mucho más atractiva y visual.
76
Software de Aplicación de la FFT
Ventana Menú principal de la aplicación.
Figura 6
2. Diseño de Multiplicación de números enteros de gran magnitud
à NOMBRE
Ventana de Multiplicación de números enteros de gran magnitud.
Código
Módulo_1.
Ventanas a las que llama
-Ventana de Ayuda (Info_1).
-Ventana de Salida (modaldlg).
-Ventana de Error (Error).
Descripción
77
Proyecto Fin de Carrera
La ventana de Multiplicación de números enteros de gran magnitud llamará al
módulo Multiplicacion_de_enteros.m . En la ventana se pondrán tanto los cuadros de texto
para introducir los dos números a multiplicar. También estará el cuadro de texto donde se
visualizará el resultado de la operación. El botón Multiplicar será el que ejecutará la
operación. Los iconos restantes tienes funciones diversas. VER OPERACIOES y
OCULTAR OPERACIOES se utilizarán para poder visualizar una ventana de texto donde
el usuario podrá ver los cálculos intermedios del algoritmo con más profundidad. Por
último, hay tres botones situados en la parte inferior de la ventana. Salir que sirve para que
desaparezca la ventana apareciendo una ventana de salida con opciones, el botón Limpiar
datos que borrará los números que aparecen en los tres cuadros de texto donde se
introducen los dos números enteros y el del resultado, el tercero es el de Ayuda que ofrece
al usuario información sobre cómo interactuar por la ventana, con instrucciones bien
enumeradas y simples. Si el usuario introduce los datos erróneamente se visualizará una
ventana de Error.
78
Software de Aplicación de la FFT
Ventana Multiplicación de números enteros.
Figura 7
3. Diseño de Multiplicación de polinomios de cualquier grado
à NOMBRE
Ventana de Multiplicación de polinomios de cualquier grado.
Código
Módulo_2.
Ventanas a las que llama
-Ventana de Ayuda (Info_2).
-Ventana de Salida (modaldlg).
Descripción
La ventana de Multiplicación de polinomios es similar a la anterior. Llamará al
módulo Multiplicacion_de_polinomios.m, y dispondrá de tres cuadros de texto para la
introducción de polinomios y la visualización de resultado. La operación de Multiplicación
79
Proyecto Fin de Carrera
se ejecutará cuando el usuario presione al botón Multiplicar situado en la parte superior
derecha de la ventana. VER OPERACIOES y OCULTAR OPERACIOES servirán para
que se visualicen las operaciones intermedias del algoritmo. Por último, se pondrán tres
botones en la parte inferior derecha de la ventana, el de Salir que sirve para salir de la
ventana, Limpiar datos, eliminará los datos introducidos por el usuario en los cuadros de
texto, y además borra el resultado para que se puedan introducir otros datos, y el tercer
botón será el de Ayuda, que dispondrá de información detallada de cómo funciona este
módulo de forma sencilla y enumerada.
Ventana Multiplicación de polinomios.
Figura 8
4. Diseño de Aproximación rápida de Chebyshev
80
Software de Aplicación de la FFT
NOMBRE
Ventana de Aproximación rápida de Chebyshev.
Código
Módulo_4.
Ventanas a las que llama
-Ventana de Ayuda (Info_4).
-Ventana de Salida (modaldlg).
-Ventana de Error (Error).
-Ventana de Información funciones (Info).
Descripción
La ventana de Aproximación rápida de Chebyshev llamará al módulo
Aprox_Chebyshev.m . En la parte superior derecha se visualizará tanto la función que
introduce el usuario, como el intervalo y el número de puntos. Con ellos el módulo operará
dando la aproximación. Esto ocurre al pulsar el botón Chebyshev. Dando a VER
OPERACIOES u OCULTAR OPERACIOES se podrán ver los cálculos que el algoritmo
ha realizado hasta obtener el resultado final. El botón Información, resuelve al usuario
dudas sobre la introducción de funciones en MATLAB, apareciendo en una ventana aparte.
El botón Ayuda ofrece al usuario las claves para poder moverse con soltura por la ventana y
realizar las operaciones. Finalmente los iconos de Salir y Limpiar datos cumplen las
mismas funciones que en las anteriores descripciones de ventanas de la aplicación.
81
Proyecto Fin de Carrera
Ventana Cálculo de aproximación rápidas de Chebyshev.
Figura 9
5. Diseño de InterpolaciónTrigonométrica
à NOMBRE
Ventana de Interpolación Trigonométrica.
Código
Módulo_3.
Ventanas a las que llama
-Ventana de Ayuda (Info_3).
-Ventana de Salida (modaldlg).
82
Software de Aplicación de la FFT
-Ventana de Error (Error).
-Ventana de Información funciones (Info).
Descripción
La ventana de Interpolación Trigonométrica llamará al módulo IT.m. Esta ventana
se ha provisto de un eje de coordenadas donde se visualizará de forma clara la
interpolación, mostrando la función original y la interpolada de otro color. En la parte
derecha al eje se dispondrá de los elementos típicos para introducir las variables: un cuadro
de texto para escribir la función o vector, otro para el intervalo, un tercero para el número
de puntos y la última opción será una pestaña para ejecutar las operaciones eligiendo Vector
o Función. También se ha puesto un botón de información de funciones MATLAB que
abrirá una ventana visualizándose todas las funciones de interés. Como en todas las
ventanas se verá un botón de OCULTAR OPERACIOES y VER OPERACIOES vara
visualizar las operaciones intermedias y el resultado. También se contará con el botón de
Ayuda para tener claras las operaciones y pasos a realizar, el botón de Limpiar datos para
introducir nuevas operaciones y el botón Salir que cerrará la ventana de Interpolación
Trigonométrica. La ventana de Error se ejecutará al introducir mal alguno de los elementos
de entrada como el intervalo, número de puntos, etc.
83
Proyecto Fin de Carrera
Ventana Interpolación Trigonométrica.
Figura 10
6. Diseño de Información sobre funciones
à NOMBRE
Ventana de Información sobre funciones en MATLAB.
Código
Info.
Descripción
Se ha pensado en los usuarios que no han interactuado nunca con el lenguaje
MATLAB, por eso se ha construido una simple ventana donde se informa al usuario cómo
se escriben algunas funciones con las que normalmente se trabaja. Esta opción solo
aparecerá en los módulos donde el usuario tenga que introducir una función de cualquier
84
Software de Aplicación de la FFT
tipo.
Ventana Información.
Figura 11
7. Diseño de Ayuda
à NOMBRE
Ventana de Ayuda.
Código
Info_1 , Info_2 , Info_3 , Info_4 .
Descripción
En cada uno de las ventanas principales se han añadido un botón de Ayuda, que
muestra la información necesaria para navegar por la ventana que el usuario tiene abierta.
85
Proyecto Fin de Carrera
En la ventana de ayuda se describe, de forma enumerada, cada paso que el usuario tiene que
realizar para hacer correctamente las operaciones y ejecutar el programa satisfactoriamente.
Ventana de Ayuda.
Figura 12
8. Diseño de Error
à NOMBRE
Ventana de Error.
Código
Error.
Descripción
Cuando el usuario cometa un error al introducir datos en el programa aparecerá esta
ventana de error explicando el problema detalladamente al usuario.
86
Software de Aplicación de la FFT
Ventana de Error.
Figura 13
9. Diseño de Salida
à NOMBRE
Ventana de Salida.
Código
modaldlg.
Descripción
Aparecerá esta ventana cuando el usuario desee salir de cualquiera de los módulos
del programa o también cuando quiera cerrar la aplicación completamente.
Ventana Salir.
Figura 14
87
Proyecto Fin de Carrera
11. Valoración económica
11.1. Introducción
En este apartado se detalla la valoración económica o análisis de costes de cada una
de las tareas/actividades que comprenden la realización y puesta en funcionamiento del
presente proyecto.
El proyecto se ha descompuesto en actividades y tareas, indicadas como partidas o
ítems en la valoración económica.
11.2. Técnicas de estimación de costes
Las diferentes partidas o ítems que componen el proyecto y que se han incluido en
este análisis de costes se detallan a continuación.
1.
Especificaciones y Desarrollo Software
Esta partida o ítem se ha dividido en dos grandes fases debido a su gran alcance e
importancia.
En primer lugar, aparece la fase de requisitos. Esta fase incluye las fases de
especificación de requisitos, del análisis funcional y del plan de pruebas.
En segundo y último lugar, se indica la fase de desarrollo del software. Esta fase es
sin duda la que ha supuesto más coste, en términos de tiempo, y la que distingue el
presupuesto del de otro proyecto que comprenda el mismo ámbito o sea del mismo tipo.
Para cada una de las fases anteriores se reseñan los costes directos, expresados en
88
Software de Aplicación de la FFT
meses/hombre (meses completos dedicados para cada actividad), necesarios para acometer
cada una de ellas, indicándose la categoría del realizador: Jefe de Proyecto o
Analista/Programador. La actividad del Jefe de Proyecto se ha estimado en un 14% respecto
de la actividad del Analista/Programador.
Por último, cabe destacar que no debe haber confusión con el significado de los
costes unitarios aquí expresados. Estos costes representan la valoración económica que
haría la empresa por poner a cargo de este proyecto a dicho Jefe de Proyecto o Analista en
su caso.
2.
Instalación, Pruebas e Integración del Software
En este apartado se recogen los costes directos de las actividades de integración y de
pruebas del software en el entorno de desarrollo y en el de explotación, incluidos los gastos
adicionales, tales como los desplazamientos y las dietas. Estos costes han sido calculados
del mismo modo que en el apartado anterior.
3.
Equipamiento y Licencias Software
Costes de todo el equipamiento e infraestructura (PCs, impresoras, RAL,
comunicaciones), si fuera necesario. Asímismo, se han de especificar en este apartado las
licencias necesarias para el entorno de explotación.
Para la implementación de este software sólo es necesario de una licencia del
lenguaje numérico y simbólico de MATLAB®, en concreto de la versión 7.0 aquí utilizada,
y disponer de un PC. Cómo la venta de este software será con toda seguridad a una persona
89
Proyecto Fin de Carrera
jurídica no se contempla en este presupuesto la adquisición de dicha plataforma hardware,
debido a que en los tiempos presentes cualquier empresa o persona jurídica dispone de un
PC, haciéndose sólo referencia a la licencia del MATLAB®.
4.
Apoyo logístico (Formación)
En este concepto se ampara la formación a impartir a los posibles operadores y
administradores del sistema a implantar. Se incluye en la formación la entrega de toda la
documentación necesaria para el curso de formación.
5.
Incrementos e IVA
Se parte de la suma de las partidas (1), (2), (3), y (4) formando el Coste Directo del
Proyecto. A este Coste Directo se le aplican los Gastos Generales H13 %L y el Beneficio
Industrial H6 %L. La suma de los conceptos de Coste Directo, Gastos Generales y Beneficio
Industrial constituyen el Total Importe sin IVA.
A este importe se le sumarán los impuestos correspondientes como IVA H16 %L,
para la Península y Baleares, IGIC H5 %L para las islas Canarias o IPSI H3 y 4 %L para Ceuta
y Melilla, respectivamente.
Total Proyecto
La suma del Total Importe sin IVA más la partida de Incrementos e IVA determinan
el importe total del desarrollo, implantación y puesta en servicio del proyecto.
90
Software de Aplicación de la FFT
11.3. Costes del proyecto
En función de lo explicado en el apartado de técnicas de estimación de costes y de
la planificación vista en apartados anteriores se procede a calcular los costes estimados del
presente proyecto.
El importe total del proyecto asciende a 23.650, 72 € (VEI@TITRÉS MIL
SEISCIE@TOS CI@CUE@TA MIL CO@ SETE@TA Y DOS CÉ@TIMOS), impuestos
incluidos.
El detalle de cada una de las partidas vistas en el apartado anterior, se expresa en la
tabla siguente:
91
Proyecto Fin de Carrera
SOFTWARE de Aplicación de la Transformada Rápida de Fourier
Ítem
1
Concepto
P.1
Empresa
Unidad
(Meses/
Hombre)
Coste
Unitario €
Coste Total
€
Total por
partidas €
Especificaciones y Desarrollo Software
a) Especificaciones
P.1.1.1
P.1.1.2
Especificación de Requisitos y Análisis Funcional
Jefe de Proyecto
Desarrollo Inf.
0,04
8.700,70
304,52
Analista/Programador
Desarrollo Inf.
0,25
6.388,78
1.597,19
Jefe de Proyecto
Desarrollo Inf.
0,04
8.700,70
304,52
Analista/Programador
Desarrollo Inf.
0,25
6.388,78
1.597,19
Jefe de Proyecto
Desarrollo Inf.
0,14
8.700,70
1.218,10
Analista/Programador
Desarrollo Inf.
1,00
6.388,78
6.388,78
Plan de pruebas
b) Desarrollo software
P.1.1.3
Ajuste de Curvas Lineal.
Multiplicación de números enteros de gran magnitud.
Multiplicación de polinomios de cualquier grado.
Interpolación Trigonométrica.
Aproximación rápida de Chebyshev.
Subtotal 1
2
P.1.2.1
P.1.2.2
Instalación, Pruebas e Integración del Software
Pruebas de integración en fábrica
(Entorno de Desarrollo)
Jefe de Proyecto
Desarrollo Inf.
0,01
8.700,70
121,81
Analista/Programador
Desarrollo Inf.
0,10
6.388,78
638,88
Jefe de Proyecto
Desarrollo Inf.
0,01
8.700,70
121,81
Analista/Programador
Desarrollo Inf.
0,10
6.388,78
638,88
Instalación y pruebas de aceptación en las instalaciones del
cliente
(Entorno de Explotación)
Subtotal 2
3
P.1.3.1
P.1.4.1
MATHWORKS
1
1.410,71
1.410,71
Apoyo Logístico (Formación)
Formación Aplicación Software y documentación
(Curso de 6 horas a 4 personas)
Desarrollo Inf.
1
2.790,83
1.410,71
2.790,83
Subtotal 4
TOTAL COSTE DIRECTO
5
1.521,37
Equipamiento y Licencias
Licencia de MATLAB V. 7.0 para Windows 10 usuarios con
Signal Processing Toolbox, Image Processing Toolbox,
Fuzzy Logic Toolbox y Wavelet Toolbox.
Mantenimiento por 1 año.
Subtotal 3
4
11.410,31
2.790,83
17.133,23
Incrementos e IVA
P.1.5.1
Gastos Generales
Desarrollo Inf.
13%
17.133,23
2.227,32
P.1.5.2
Beneficio Industrial
Desarrollo Inf.
6%
17.133,23
1.027,99
TOTAL IMPORTE SIN IVA
IVA (Península y Baleares)
16%
20.388,55
3.262,17
TOTAL PROYECTO (EUROS)
92
20.388,55
23.650,72
Software de Aplicación de la FFT
12. Conclusiones y líneas futuras
Durante el desarrollo de este proyecto, en el que se ha aplicado el conocimiento de
los algoritmos de la Trasformada Rápida de Fourier HFFTL para su utilización práctica en
diferentes problemas científicos, se ha comprobado que su programación ha sido ardua pero
muy eficiente en su aplicación práctica a problemas concretos.
La Trasformada Rápida de Fourier HFFTL es un algoritmo muy complejo que
requiere una base matemática para su comprensión así como un conocimiento de la
Transformada Discreta de Fourier HTDFL. En consecuencia, su aplicación práctica a los
problemas técnicos-científicos planteados como objetivos de este proyecto va más allá del
diseño e implementación de un software concreto. Esta razón ha guiado el desarrollo del
presente proyecto, abrigando la esperanza de clarificar los fundamentos de la FFT, así como
su amplia y la diversa aplicación de estos algoritmos en los diferentes casos que se han
propuesto, facilitando un conocimiento pedagógico de un tema árido, si se analiza desde un
punto de vista únicamente matemático.
Por consiguiente, tras hacer un amplio recorrido por los fundamentos matemáticos
de las aplicaciones de la FFT a diversos problemas técnicos, y tras haber analizado y
programado los algoritmos empleados para resolver el problema concreto tratado, se
establecen las conclusiones teóricas y prácticas enunciada a continuación:
1.
Multiplicación de números enteros de gran magnitud.
93
Proyecto Fin de Carrera
Se ha aplicado satisfactoriamente la FFT a este problema, aunque se ha encontrado
en un principio dificultades ya que no se encontraba información técnica sobre este tema. A
raíz de la teoría de la convolución, explicada en este proyecto, se ha investigado y estudiado
hasta llegar a los resultados fijados en los requisitos. En contra de lo que cabría pensarse se
han encontrado dificultades por parte del programa con el que se estaba programando, al no
obtenerse con precisión las últimas cifras menos significativas del resultado. Esto es debido
a que este lenguaje, aun operando internamente con números enteros de 16 dígitos
decimales de precisión, al representarlos en el mayor formato posible, realiza una operación
de truncamiento en su representación, visualizándolos en notación científica.
El algoritmo diseñado cumple con los objetivos, pero con el inconveniente que el
resultado vendrá truncado por la limitación de la representación simbólica del lenguaje
MATLAB.
2.
Multiplicación de polinomios de cualquier grado.
En este módulo se ha tenido también que aplicar la teoría de la convolución, y al
contrario del anterior, esta aplicación se ha desarrollado de manera más fácil, pudiéndose
usar la FFT de manera exitosa y obteniendo los resultados esperados. El problema ha sido
convertir los coeficientes del polinomio, que son los que se obtienen cuando se realizan las
operaciones, en formato simbólico para su representación tanto en la interfaz de usuario
como para crear el polinomio resultado como una expresión simbólica.
Otro problema resuelto ha sido el verificar que el usuario ha introducido
correctamente un vector, dado que este lenguaje no dispone de funciones que facilite su
94
Software de Aplicación de la FFT
comprobación. Se ha resuelto explicando al usuario cómo debe introducir las expresiones
de forma gráfica y sencilla.
3.
Interpolación Trigonométrica.
Se ha desarrollado la interpolación una función dada en dos intervalos posibles:
@-p , p D y @0 , 2 pD de manera satisfactoria, introduciendo cualquier función siempre con
un número par de puntos. La interpolación de un vector de puntos en lugar de una función
concreta también funciona con precisión, si bien el número de puntos tiene que ser potencia
de dos, debido al algoritmo de la FFT. En este módulo, por el contrario, se verifica que
todos los datos introducidos son correctos. El problema de las variables simbólicas, como
en el módulo anterior, se ha solucionado de la misma forma.
4.
Aproximación rápida de Chebyshev.
Este módulo ha sido el más complicado de diseñar y programar, puesto que no se
han encontrado suficientes artículos o publicaciones que lo traten. No obstante, con la
bibliografía de referencia y con los problemas ya resueltos, se ha conseguido un algoritmo
que proporciona una aproximación coherente y satisfactoria. Además, esta aproximación se
realiza en el intervalo @-1, 1D.
5.
Interfaz gráfica de la aplicación software.
Con la funcionalidad GUIDE de MATLAB se ha podido diseñar y programar una
interfaz gráfica sencilla y visual, que cumple sobradamente con los objetivos del proyecto,
ya que posee todos los elementos necesarios para interactuar con la aplicación.
95
Proyecto Fin de Carrera
Permite esta interfaz aprender y aplicar los algoritmos de la FFT en los campos ya
mencionados, de un modo inteligible y eminentemente práctico.
6.
Como línea futura de análisis e investigación y como mejora posible a introducir al
actual proyecto cabría reseñar:
a)
Incluir en el módulo de Interpolación Trigonométrica las gráficas que
representen la función error cometido entre la función y el polinomio interpolador
trigonométrico.
b)
Ampliar el módulo de la Aproximación rápida de Chebyshev para incluir la
gráfica de la función error.
c)
Diseño, programación e implementación de las siguientes aplicaciones
prácticas de la FFT:
ä
Cálculo de un vector por una matriz Toeplitz empleadas en el
procesamiento de señales.
ä
Obtención del producto de una matriz circulante y un vector.
ä
Resolución de un sistema lineal Circulante.
ä
Aplicación en la Transformada Rápida Discreta del Seno HDSTL y en
Transformada Rápida Discreta del Coseno HDCTL.
96
Software de Aplicación de la FFT
ä
Utilización de FFT en la Transformada Rápida Discreta de Hartley HDHTL.
ä
Resolución de Ecuaciones Diferenciales.
97
Proyecto Fin de Carrera
13. Bibliografía
La siguiente relación de libros y artículos incluye el material de consulta que se ha
utilizado para la realización de este proyecto. Están listados por orden alfabético de
referencias. Las referencias se componen de cuatro letras y dos numéricos. Las cuatro letras
hacen referencia al autor/es siendo las cuatro del primer apellido del autor, o si fuesen
varios, las cuatro primeras letras del primer apellido del autor que figuran en primer lugar.
Los dígitos corresponden con el año de la primera publicación.
La relación de consultas es la siguiente:
[BARR01]
Barranco de Areba, Jesús
Metodología de análisis estructurado de sistemas.
Ed UPCO. Madrid 2001.
[CHUE00]
Chu Eleanor, George Alan.
Inside the FFT Black Box.
Ed CRC Press LLC .United States of America, 2000.
[CUYP04]
Cuypers Gert ,Ysebaert Geert, Moonen Marc, Pisoni Fabio.
98
Software de Aplicación de la FFT
Chebyshev and Fourier Espectral Methods.
Katholieke Universiteit Leuven, Published in proc. IEEE ICC, 2004.
[DOMI05]
Domínguez Víctor, Rapún María Luisa.
Funciones como argumento. Recursividad Fórmulas de cuadratura. FFT.
Ed Univerrsidad de Navarra.Navarra, 2005.
[GARC05]
García de Jalón, José Ignacio Rodríguez, Vidal Jesús.
Aprenda matlab 7.0 como si estuviera en primero..
Ed. Escuela Técnica Superior de Ingeniería Industrial. Madrid 2005.
[GARC98]
García Alfonso, García Fernando, Gutiérrez Andrés,
López Antonio, Rodríguez Gerardo, De la Villa Agustín.
Cálculo I, Teoría y Problemas de Análisis matemático en una variable.
Ed. CLAGSA. Madrid, 1998, 2ª Edición.
[BOYD00]
Boyd, John.P.
Chebyshev and Fourier Espectral Methods.
Dover Publications, Inc.United States of America, 2000.
[RI@C01]
Rincón, F.
99
Proyecto Fin de Carrera
Análisis Matemático y Métodos uméricos para Informática.
Ed. Dpto. Publicaciones de la E.U.I. Madrid, 2001.
[RODR03]
Rodríguez Gómez, Fco. Javier.
Cálculo y Métodos úmericos. Teoria, Algoritmos y Problemas Resueltos
Ed. UPCO. Madrid 2003.
[ZULE06]
Zuleta Marzal Victoria.
Algoritmos y Aplicaciones de la transformada rápida de Fourier.
Proyecto fin de carrera, UPCO, Madrid, 2006.
URL's de Interés
[1] http://toyscaos.tripod.com/matlab7.html
[2] http://www.mathworks.com/
[3] http://en.wikipedia.org/wiki/Chebyshev_polynomials
[4] http://en.wikipedia.org/wiki/Discrete_cosine_transform
[5] http://www.hydrogenaudio.org/forums/lofiversion/index.php/t39574.html.
100
Software de Aplicación de la FFT
Anexo I. Programación y guía de
instalación
En esta parte se tratará de las bibliotecas y dentro de ellas las funciones que ha
utilizado MATLAB para realizar las operaciones en los diferentes módulos del programa.
Por otro lado se detallará una pequeña guía de instalación de la aplicación, para que
ayude al usuario a instalarla con éxito y pueda finalmente ejecutarla.
101
Proyecto Fin de Carrera
I.1 Bibliotecas y Funciones MATLAB
La bilioteca MATLAB C Math Library proporciona al usuario la capacidad para
programar con MATLAB en una biblioteca con formato objeto enlazable. El principal
objetivo de la C Math Library es soportar el desarrollo de aplicaciones que se puedan
ejecutar y controlar por el operador como entidades independientes de cualquier otra,
utilizando con ellos MATLAB y su compilador.
Proporciona una amplia variedad de funciones clásicas del programa MATLAB,
que se incluyen como bibliotecas objeto, abarcando entre otras las categorías siguientes en
el entorno MATLAB y archivos M compilados:
ä
Funcionales especiales y elementales.
ä
Álgebra lineal numérica.
ä
Polinomios e interpolación.
ä
Métodos numéricos no lineales.
ä
Estadística y análisis de Fourier.
ä
Operaciones algebraicas y lógicas.
Los algoritmos que se utilizan en esta biblioteca han sido desarrollados por un
grupo de renombrados expertos en programación algorítmica de funciones de tipo
matemático (álgebra lineal y cálculo numérico). Obteniéndose muchas de ellas de las
bibliotecas mundialmente reconocidas LINPACK y EISPACK. La biblioteca MATLAB C
102
Software de Aplicación de la FFT
Math Library contiene más de 300 funciones numéricas, lógicas y de utilidad. Todas estas
funciones permiten operar con datos de tipo escalar, vectorial o matricial con la misma
facilidad sintáctica.
En especial se hablará de la biblioteca FFTW (llamada antes Estadística y análisis
de Fourier) que posee la C Math Library. Esta biblioteca contiene todos los algoritmos de la
FFT utilizados en el proyecto. Posee las siguientes funciones:
fft
Trasformada Discreta de Fourier.
fft2
Transformada Discreta de Fourier de dos dimensiones.
fftn
Transformada Discreta Multidimensional.
fftshift
Reordena el vector X en orden creciente de frecuencia.
ifft
Inversa de la Trasformada Discreta de Fourier.
ifft2
Inversa de la Transformada Discreta de Fourier de dos dimensiones.
ifftn
Inversa de la Transformada Discreta Multidimensional.
Las únicas dos que se han utilizado son la fft e ifft, para ayudar a hacer las
operaciones que eran necesarias. En las dos funciones los argumentos de entrada son un
vector de n elementos, y el argumento de salida ha sidoa un vector de números complejos
de n elementos, siendo la trasformada del vector x introducido.
Otra de las biblioteca más utilizadas ha sido <string.h>. Contiene todas las
funciones relacionadas con el formato string. Se ha tenido que trabajar con ellas ya que
103
Proyecto Fin de Carrera
MATLAB no permite intoducir en un fichero de texto variables simbólicas, teniéndose que
trasformar en caracteres todas las funciones resultantes de los módulos.
strcpy
Copia una cadena.
strcat
Concatena dos cadenas de caracteres.
strcmp
Compara dos cadenas o una cadena con un vector de strings, devolviendo 1
si es cierto y son iguales y 0 si no lo son.
Por último, comentar que la interfaz <matplotlib.pylab> es la biblioteca que permite
a MATLAB dibujar gráficas de funciones o de puntos. Es una de las bibliotecas más
potentes que posee y contiene multitud de funciones relacionadas con el dibujo 2-D y 3-D .
Se han utilizado en el proyecto un gran número de ellas entre las se destacan:
plot
Dibuja una gráfica.
axes
Crea un eje.
title
Pone un nombre al eje.
zoom
Amplía la función al apretar en un punto de ella.
hold
Tiene dos posiciones Off y On. Mantiene la función para poder dibujar otra
encima.
grid
Dibuja una cuadrícula.
xlabel
Crea una etiqueta en el eje x.
104
Software de Aplicación de la FFT
ylabel
Crea una etiqueta en el eje y.
I.2 Guía de instalación del software
MATLAB V.7 (R14)
Este va a ser el programa que va a ser necesario para ejecutar la aplicación al
completo. Es necesario instalar el programa entero y no una versión de prueba, ya que se
necesita instalar la colección completa de biblioteca que posee. Una vez instalado se
procederá a explicar cómo ejecutar el programa.
Se entregará la aplicación completa en un CD-ROM junto con la carpeta
denominada PFC_FFT. En dicho directorio se encuentran todos los archivos con extensión
.m y extensión .fig necesarios para ejecutar el programa. Además en PCF_FFT se guardarán
todos los documentos de texto que se generarán en la aplicación para poder usarlos en
cualquier momento.
A continuaciuon se mostará como instalar el programa MATLAB:
(Aviso importante: Malab funciona perfectamente con todos los microprocesadores
tanto Intel como AMD, sin embargo si un ordenador usa este último se debe consultar la
página del fabricante ya que se tendrá que hacer algún paso más).
1º- Se dispondrá de una carpeta llamada MATLAB(7.0). Se accede a ella.
105
Proyecto Fin de Carrera
2º- Una vez dentro de MATLAB (7.0) se entra en la carpeta MATHLAB1 y se
ejecuta el instalador pulsando setup.
106
Software de Aplicación de la FFT
3º- Aparecerá una pantalla del sistema Windows Vista para verificar los permisos y
se pulsa permitir (si se instala en Windows XP no se necesita esta verificación). Una vez en
la pantalla de inicio de la instalación se elige la opción Install y se pulsa el botón @ext.
107
Proyecto Fin de Carrera
4º- Se procederá a poner el nombre y la compañía (se pondrá el mismo nombre para
que no haya problemas). Se continúa la instalación pulsando @ext y se mostrará una
pantalla donde se tiene que leer la licencia y dar finalmente a Yes y a continuación a @ext.
5º- A continuación, se elige la opción de instalación Typical, se pulsa @ext y
aparecerá una pantalla donde se preguntará dónde instalar el programa. Por defecto está en
C:\MATLAB7\ (se deja esta dirección por defecto), y se pulsa @ext.
108
Software de Aplicación de la FFT
6º- Seguidamente se pulsa el botón Install, y el programa empezará a instalarse. Se
verá el porcentaje. Esta operación durará varios minutos.
109
Proyecto Fin de Carrera
7º- En un momento de la instalación, aproximadamente por la mitad aparecerá una
ventana como la que se muestra a continuación.
Para completar la instalación se indica que hay que instalar el CD2. Para ello se
aprieta el botón Browser y se elige la dirección donde se encuentra la otra carpeta llamada
MATHLAB2. Se abre y se pulsa el botón Select. Para terminar se pulsa la opción OK. Con
esto hecho continuará la instalación.
110
Software de Aplicación de la FFT
8º- Por último, se pulsa la opción @ext y se concluye eligiendo el botón Finish.
Terminándose así la instalación de MATLAB.
111
Proyecto Fin de Carrera
9º- (Esta acción se tendrá que hacer cada vez que se quiera ejecutar el
programa). Con la pantalla de MATLAB abierta, en la parte superior de la ventana donde
pone Current Directory: se pulsa el icono de los puntos suspensivos y se busca la carpeta
PFC_FFT, pulsando por último el botón Aceptar.
112
Software de Aplicación de la FFT
10º- Una vez situados en la carpeta PFC_FFT se estará preparado para iniciar el
programa con éxito. Se ejecuta escribiendo en la pantalla principal del entorno MATLAB,
llamada Command Windows, el texto Menu_FFT, y se pulsa Enter: el programa del
proyecto se iniciará.
113