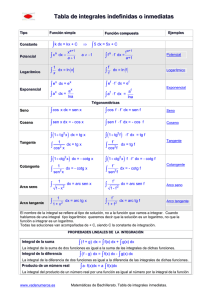
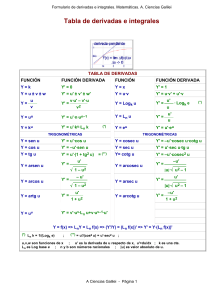
Tabla de Derivadas
Anuncio

1.2 TABLA DE DERIVADAS FUNCIONES ALGEBRAICAS Función Derivada FUNCIONES CIRCULARES INVERSAS Derivada Función y u v y u v y ku y k u y uv y u v u v y u v y u v u v y u v y y k v y y u k u v u v v2 k v v2 u y k y n u n1 u y u n y n y u n u n 1 1 n y au y a u u ln a y eu y e u u yu v y u y v u y v 1 y y arc tg u y y arc cotg u y y arc sec u y 1 1 un u v u u v ln u u u u yk y 0 yx y 1 y kx y k y x k y FUNCIONES LOGARÍTMICAS Función Derivada y k x y 1 u2 u 1 u2 u 1 u2 u u u2 1 u u u2 1 k x2 y xn y nx n 1 y x n y y x y ya u u log a e u ln a u u y u y log a u y FUNCIONES CIRCULARES Función Derivada y sen u y u cos u y cos u y u sen u y tg u y u sec 2 u y cotg u y u cosec 2 u y sec u y u sec u tg u n x n 1 x 1 2 x y a x ln a y ex y e x y xx y x x 1 ln x y log a x y 1 x ln a y ln x y 1 , x 0 x y sen x y cos x y cos x y sen x y tg x y sec 2 x dy d ; f ( x ) ; Df dx dx y cosec u y u cosec u cotg u Notaciones de la derivada : y ; f ( x ) ; Notación de Lagrange : f ( x ) ; Notación de Leibniz : Siendo las funciones: u f ( x ) y v g( x ) sec 2 u 1 1 1 tg 2 u ; cosec 2 u 1 cotg 2 u cos 2 u sen 2 u dy dx Las distintas partes de las expresiones que incluyen “dx” carecen de significado por separado, es decir, las “d” no son números y la expresión completa no es el cociente de dos números, es solo una forma de escribir la derivada de una función. MATH CHEAT SHEET ─ 3 c o n 1 4 . c o m u 1 k y ln u 1 u2 Funciones Simples Función Derivada n u u n1 n y arc cos u u y un y u y y arc cosec u y FUNCIONES POTENCIALES, EXPONENCIALES y V.A. Derivada Función 1 un y arc sen u