Agustin Martin DomingoTransmisión del calor. Física y Mecánica de

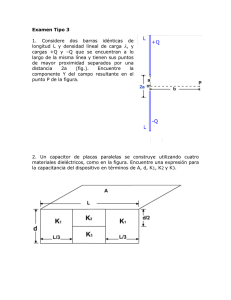
Transmisión del calor. Física y Mecánica de las Construcciones. A. Martín. Grupo B. 2010/2011.
1
Agustin Martin Domingo
1. Determínese la potencia calorífica que ha de suministrarse para mantener una habitación a la temperatura
de 24◦ C, teniendo en cuenta que pierde calor a través de una pared de piedra caliza de área total S =
40 m2 y espesor ep = 50 cm, a un medio exterior a −8◦ C. La pared está protegida interiormente por una
capa de material aislante de espesor ea = 0,5 cm de conductividad λa = 4,2 × 10−4 cal/(cm seg◦ C).
Otros datos: λp (piedra caliza) = 5,2 × 10−3 cal/(cm seg◦ C).
h(pared vertical) = 0,424 × 10−4 (∆T )1/4 cal/(seg cm2 ◦ C).
2. El aire situado sobre la superficie de un lago de agua dulce está a la temperatura TA , mientras que el agua
se encuentra en su punto de solidificación Ti (TA < Ti ). Al cabo de un cierto tiempo t se ha formado una
capa de hielo de espesor y. Suponiendo que todo el calor liberado cuando el agua solidifica fluye hacia
arriba por conducción a través del hielo y luego pasa al aire por convección, demostrar que:
y
y2
Ti − TA
+
=
t
h 2λ
ρl
donde h es el coeficiente de convección por unidad de área (o superficial), λ es la conductividad térmica
del hielo, l el calor latente de fusión y ρ la densidad del hielo.
3. Un tubo de hierro de longitud L = 20 m, diámetro interior D1 = 8 cm y exterior D2 = 9,6 cm está recubierto por una capa aislante cilíndrica de diámetro interior D2 = 9,6 cm y exterior D3 = 11,52 cm.
Por el tubo circula agua caliente que hace que la temperatura en la cara interior del tubo sea en régimen
estacionario T1 = 80◦ C. Cuando la temperatura del aire exterior, que se supone coincidente con la de la
capa de diámetro D3 del aislante es T3 = 10◦ C, y sabiendo que las conductividades térmicas del hierro y
del aislante son λh = 39 kcal/h m◦ C y λa = λh /999, respectivamente, determínese:
(a) La cantidad de calor perdida durante un día.
(b) Si el tubo sufriese dos cortes longitudinales separados 60 grados perdiendo el aislante y considerando que se pierde el contacto térmico entre las dos partes en que queda dividido el tubo interior,
calcular la pérdida de calor diaria si la temperatura de la superficie exterior de la parte que ha
perdido el aislante también es de 10◦ C.
4. Un local a las 10 de la mañana tiene una temperatura de 6◦ C siendo la temperatura exterior de 3◦ C y el
coeficiente total de transmisión del calor para paredes y techo U = 1,3 kcal/m2 h◦ C. El local tiene una
superficie total (paredes y techo) A = 100 m2 . Se enciende la calefacción que suministra una potencia
calorífica Φ = 50∆T kcal/h, siendo ∆T la diferencia de temperatura entre la placa de calefacción que
está a 70◦ C y la del local. Calcular:
(a) La temperatura de equilibrio de la habitación.
(b) Si la capacidad calorífica de la habitación es de Cp = 15 kcal/grado, ¿a qué hora se habrá alcanzado
la temperatura de 20◦ C?
5. En el interior de una canalización cilíndrica de acero (λ = 16 W/m◦ C) de radios R1 = 0,2 m y R2 =
0,25 m circula un fluido a una temperatura Ti = 80◦ C, cuando el medio exterior se encuentra a una temperatura Te = 20◦ C. Determínese:
(a) Coeficiente global de pérdidas por unidad de longitud en W/m◦ C.
(b) La distribución radial de temperatura en el tubo de acero.
(c) El espesor de una capa de aislante de conductividad térmica λa = 0,030 kcal/mh◦ C para que las
pérdidas se reduzcan a la cuarta parte.
siendo los coeficientes de intercambio de calor por convección en el interior y en el exterior de
hi = 8 kcal/m2 h◦ C y he = 4 kcal/m2 h◦ C respectivamente.
6. Se pierde calor a través de un cerramiento compuesto por un muro de fábrica de 20 cm de espesor y de
una capa aislante de 4 cm de espesor. Si la temperatura exterior es de −18◦ C, la habitación está a 20◦ C,
y los coeficientes de convección interior y exterior son hi = 10−4 cal/(s·cm2◦ C) y he = 2hi , determinar,
suponiendo régimen permanente:
Transmisión del calor. Física y Mecánica de las Construcciones. A. Martín. Grupo B. 2010/2011.
a)
b)
La energía calorífica perdida por unidad de tiempo y de superficie.
La conductividad que debe tener un aislante del mismo espesor que el anterior para que el mismo
muro de fábrica, pero de espesor 10 cm, tenga las mismas pérdidas.
Las temperaturas de las superficies exterior e interior del muro compuesto y la temperatura de la
superficie de contacto entre los dos materiales.
Agustin Martin Domingo
c)
2
Datos: Conductividad térmica del muro de fábrica 0,0141 cal/(cm·s·◦ C), conductividad térmica del aislante 5 · 10−4 cal/(cm·s·◦ C)
7. Una habitación tiene un cerramiento exterior de 2×2,40 m, que se compone de una ventana de 1×1,2 m2
y coeficiente global de transmisión térmica 4 W/m2◦ C, y de un muro de coeficiente global de transmisión
térmica 0,5 W/m2◦ C. El resto de paredes interiores dan a otras habitaciones de la casa que se encuentran a la misma temperatura de la habitación considerada. El coeficiente global de transmisión del calor
de suelo y techo es de 1 W/m2◦ C y sus dimensiones de 3 × 2 m2 . El piso superior se encuentra a una
temperatura de 26◦ C y el inferior a una temperatura de 23◦ C, mientras que la calle se encuentra a una
temperatura de 5◦ C. En régimen estacionario, calcular:
(a) Temperatura de la habitación.
(b) Pérdidas de calor por unidad de tiempo a través de la ventana.
(c) ¿Que potencia deberá tener una calefacción colocada en la habitación para que la temperatura en
la misma sea de 20◦ C? Para este apartado supóngase que las demás habitaciones de la casa tienen
en todo momento la misma temperatura que la habitación estudiada.
Capa
1 Hormigón
2 Fibra de vidrio
3 Ladrillo
4 Yeso
Conductividad térmica
(W·m−1◦ C−1 )
1,63
0,034
0,76
0,18
Resistencia al vapor
(N·g−1 s)
14,85 × 106
1,485 × 106
1,265 × 106
0,880 × 106
Interior Ti =18◦ C
Exterior Te =0◦ C
1
2
3 4
8. Sea el cerramiento multicapa que se muestra en la figura, constituido por los materiales de la tabla adjunta. Dicho cerramiento separa el interior de un local, donde el aire está a una temperatura de 18◦ C y la presión de vapor es de 1550 Pa, del exterior, que se encuentra a una temperatura de 0◦ C con una presión de vapor de 580 Pa. En el estado estacionario, y sabiendo que
los coeficientes superficiales convectivos interior y exterior son respectivamente hi = 9 W·m−2◦ C−1 y he = 17 W·m−2◦ C−1 , determinar:
(a) El flujo de calor por unidad de superficie a través del cerramiento.
(b) El flujo de vapor por unidad de superficie a través del cerramiento si no hubiera condensaciones.
(c) ¿Se producirán condensaciones superficiales? y de producirse, ¿dónde? ¿Y condensaciones
intersticiales, y dónde?
Espesor
(m)
0,15
0,18
0,04
0,015
9. Una esfera maciza de cobre ennegrecido, de radio 2 cm, se coloca dentro
de una cavidad en la que se ha hecho el vacío y cuyas paredes se mantienen a 100◦ C. ¿Que cantidad de energía ha de suministrarse por segundo
a la esfera para mantener su temperatura constante e igual a 127◦ C?
10. La temperatura de un filamento de wolframio es de 2450 K y su emisividad total 0,30. Calcular la superficie del filamento de una lámpara de 25 W?
11. La superficie de un tejado tiene un coeficiente de absorción α = 0,95 para la radiación solar y una emisividad o coeficiente de emisión ǫ = 0,1. En un determinado momento del día, la radiación solar incidente
es de 750 W/m2 y la temperatura de la superficie de 120◦ C. Determínese la potencia por unidad de superficie que absorbe ésta en esas condiciones.
Transmisión del calor. Física y Mecánica de las Construcciones. A. Martín. Grupo B. 2010/2011.
3
Agustin Martin Domingo
12. Estimar la máxima temperatura que alcanza, con tiempo despejado el día 21 de junio, una azotea horizontal situada a 45◦ de latitud norte (en estas condiciones, los rayos solares incidentes forman un ángulo
de 22◦ con la vertical). Se supone que la única radiación existente es la del Sol y que el coeficiente de
transmisión del calor por convección es de 9,75 kcal/h◦ C m2 . Se admite que la temperatura del aire ambiente es de 38◦ C y se consideran los casos:
(a) La azotea es perfectamente negra.
(b) La azotea está recubierta de aluminio, cuyo coeficiente de absorción para la radiación solar es 0,3
y su emisividad a la temperatura de la azotea es 0,07. Despreciar la absorción y dispersión por la
atmósfera.
Datos: Constante solar G = 1140 kcal/(h m2 ), hc = 0,01132 kW/(grado m2 )
R λ2
1
Fλ1 −λ2 = Rλ∞
0
1
0,8
0,6
ǫλ
13. Una superficie de ladrillo a la temperatura T = 500 K tiene el siguiente coeficiente de emisión hemisférico. Determinar el coeficiente de emisión total y la emitancia total
si F0−1,5 = 0,000, F0−10 = 0,634 y F0−∞ = 1, siendo:
Mλ (T )dλ
Mλ (T )dλ
0,4
0,2
con Mλ la emitancia espectral del cuerpo negro.
00 1,5
5
10
15
20
λ(µm)
14. Un pequeño orificio de área ∆A se abre en las paredes de un horno que contiene radiación a la temperatura T . Una esfera de radio r se coloca frente al orificio a una distancia R ≫ r. Determínese la expresión
de la energía que incide sobre la esfera, procedente del orificio en función de ∆A, T , R y r.
15. Suponiendo que la esfera del problema anterior es un cuerpo negro muy conductor de forma que la
temperatura de su superficie es la misma T0 en todos sus puntos, determínese cual sería su temperatura
de equilibrio si únicamente incide sobre ella la energía procedente del orificio. ¿Cómo se modifica el
problema si el coeficiente de absorción del cuerpo es α < 1 con independencia de la longitud de onda de
la radiación?
16. Considérese el Sol como una esfera de diámetro 2R = 1,39 · 106 km que irradia como un cuerpo negro con temperatura T = 5770 K, situado a una distancia d = 149 · 106 km de la Tierra, cuyo radio vale
r = 6370 km. Con estas hipótesis, determínese:
(a) Energía solar incidente sobre la tierra por segundo.
(b) Suponiendo que la Tierra se comporta como un cuerpo negro y que su temperatura no difiere
apreciablemente de un punto a otro, ¿cuánto valdría su temperatura de equilibrio T0 ?
(c) Suponiendo que la Tierra absorbe una fracción α de la energía solar y emite una fracción ǫ, ¿cuál
sería su temperatura de equilibrio?
17. Una capa de nubes muy extensa tiene su base, horizontal, a una temperatura T1 = −3◦ C y se encuentra
sobre un suelo también horizontal a T2 = 27◦ C. Suponiendo que el aire no absorbe radiación, que es de
noche, que no interviene otro mecanismo de transmisión del calor que la radiación y que suelo y nubes
se comportan como cuerpos negros, determínese la relación entre la energía perdida por el suelo y la que
perdería si la atmósfera estuviera despejada.
18. A la misma distancia del Sol se consideran dos objetos de la misma sustancia perfectamente conductora
del calor. Uno es una esfera y el otro un cubo con una de sus caras ortogonal a los rayos solares. ¿Cuál
será la relación Te /Tc entre las temperaturas de equilibrio que alcanzan la esfera y el cubo?