Stephen P. Shao (1975) STATISTICS FOR BUSINESS AND
Anuncio

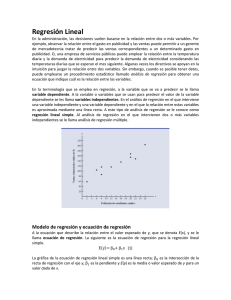
Stephen P. Shao (1975) STATISTICS FOR BUSINESS AND ECONOMICS Estadística para Economistas y Administradores de Empresas Editorial: Herrero Hermanos, SUCS., S.A. Página 669 México, D.F. CORRELACIÓN NO LINEAL, MÚLTIPLE, PARCIAL Y POR RANGOS La exposición en los dos capítulos previos estuvo basada en el supuesto de que la relación promedio entre dos variables pudo ser descrita mediante una línea recta. Sin embargo, el supuesto puede llegar a ser inadecuado para algunos datos. Es muy frecuente que la relación concerniente a las actividades de los negocios y económicas pueden ser descritas mejor mediante una curva que mediante una línea recta. El análisis de regresión y correlación no lineal se presenta en la sección 23.1. Aún más, una variable dependiente puede estar relacionada o asociada no solamente con una variable independiente sino también con dos o más variables independientes. El análisis de la relación entre tres o más variables se presenta en las secciones 23.2 y 23.3 concerniente a la correlación múltiple y parcial. Además, dos variables relacionadas pueden ser expresadas en números ordinales o de rango. La medida de correlación por rangos es expuesta en la sección 23.4. 23.1 REGRESIÓN Y CORRELACIÓN NO LINEAL Esta sección presentará el análisis de la regresión y correlación no lineal basado en 1) una curva parabólica determinada mediantes una ecuación polinomial de segundo grado, 2) una curva suave dibujada mediante el método gráfico a mano alzada y 3) una línea quebrada calculada para datos agrupados mediante una tabla de correlación. Curva parabólica de segundo grado Esta curva de regresión está basada en la ecuación polinomial de segundo grado, presentada en el capítulo 18, p 531. 𝐘𝐜 = 𝒂 + 𝒃𝑿 + 𝒄𝑿𝟐 Los tópicos incluidos usualmente en el análisis de regresión y correlación, basado en la curva parabólica de segundo grado, son como sigue: a) Dibujar el diagrama de esparcimiento sobre una gráfica. b) Calcula la ecuación de regresión 𝐘𝐜 = 𝒂 + 𝒃𝑿 + 𝒄𝑿𝟐 . c) Dibujar sobre la gráfica la curva de regresión, basados en la ecuación de arriba. d) Calcular la desviación estándar de regresión mediante la fórmula presentada en el capítulo 21. (p. 621) (Y Yc) 2 Sy / x n