Capitulo 7 Reacciones Heterogeneas

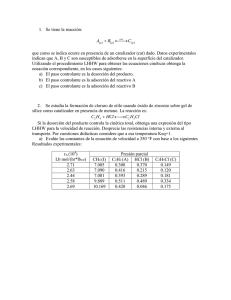
Capítulo 7 - Reacciones Heterogéneas
1
________________________________________________________________________________________________________
-----------7.- Reacciones Heterogéneas.
7.1.- Introducción.
Una gran cantidad de procesos industriales, se llevan a cabo mediante reacciones que
no son homogéneas, es decir, presentan más de una fase.
Estas reacciones no son tan fáciles de estudiar como las reacciones homogéneas, ya
que los procesos físicos involucrados muchas veces son más complejos que la reacción química
en sí misma. En muchos casos también ocurren cambios de fases tales como el paso de sólido a
líquido durante la reducción de los minerales a metales fundidos en las industrias metalúrgicas.
Aún más difíciles de analizar son las reacciones enzimáticas.
La velocidad global de una reacción heterogénea dependerá, además de la afinidad
química, de otros factores, entre los cuales podemos mencionar:
a.- El área de la superficie de interface.
La velocidad de reacción química es proporcional a la superficie de la interface. Una
gran superficie se consigue, normalmente, mediante la molienda de la materia prima. Sin
embargo, no siempre una granulometría muy fina es conveniente, a pesar de su gran
superficie tal es el caso de la obtención de cal, salvo que sea un horno que opere con
lecho fluidizado.
b.- Las velocidades de difusión de los reactivos hasta la interface.
Este factor está fuertemente afectado por las velocidades relativas de las dos fases,
por la presión de la fase fluida, y en menor grado, por la temperatura del sistema y de las
propiedades físicas de los reactivos y sus formas geométricas.
c.- La velocidad de los productos para retornar a la fase fluida.
Este factor tiene especial importancia en las reacciones reversible. En los
regímenes turbulentos o muy agitados este efecto se ve notablemente reducido.
Por lo expuesto, en la determinación de la forma de la ecuación cinética, se deberán
tener en cuenta no solo la velocidad de reacción química en sí, sino también las velocidades de
transporte de materia.
Normalmente, uno de los dos pasos es más importante que el otro, ya que la velocidad
de transferencia de materia y la de reacción química serán una menor que la otra, y esta será la
que controla el proceso.
7.2.- Tipos de Reacciones Heterogéneas.
Las reacciones heterogéneas pueden clasificarse en base a muchos criterios, siendo el
más usual el siguiente:
a.- Reacciones No Catalíticas.
b.- Reacciones Catalíticas.
Capítulo 7 - Reacciones Heterogéneas
2
________________________________________________________________________________________________________
Dentro de estos dos tipos las reacciones pueden clasificarse por el tipo de fases que
intervienen en la reacción:
a.- Gas – Líquido.
b.- Líquido - Líquido (Inmiscibles).
c.- Gas – Sólido.
d.- Líquido - Sólido.
e.- Sólido – Sólido.
f.- Gas – Sólido – Líquido.
Ninguno de estos tipos de reacciones tienen teorías simples y completas que describan
el comportamiento de los reactivos y productos.
7.2.1.- Cinética de las Reacciones Heterogéneas.
Si bien las reacciones químicas catalíticas tienen mecanismos diferentes a los de las no
catalíticas, desde el punto de vista global de la reacción se pueden identificar pasos o etapas que
son comunes y otros que son particulares de cada una de ellas.
En general, se pueden identificar las siguientes etapas:
1.- Difusión de las moléculas desde la masa de fluido hasta la superficie o interface (transporte de
materia).
2.- Adsorción de los reactivos.
3.- Reacción química de superficie.
4.- Desorción de los productos.
5.- Transporte de los productos desde la superficie hacia el seno de la masa fluida.
Alguna o algunas de estas etapas pueden ser más o menos importantes en algunos tipos
de reacciones, e incluso una o varias pueden no presentarse en algunas de ellas.
Es necesario por lo tanto estudiar cada una de las etapas para cada uno de los
diferentes tipos de interfaces que se pueden presentar en las reacciones heterogéneas. Sin
embargo, solamente se analizarán aquellos casos que se presentan con mayor frecuencia en la
industria de procesos.
En general, en las reacciones no catalíticas tienen mucha importancia las etapas 1.-, 3.y 5.-, mientras que en las reacciones catalíticas todas tienen o pueden tener importancia, según
sea el tipo de catalizador utilizado.
7.2.1.1.- Velocidad de Transporte de Materia por Difusión.
Aunque los cálculos se realizarán para el caso de dos fluidos inmiscibles, los coeficientes
de transferencia y las ecuaciones de la velocidad de difusión, son válidas también para el caso de
sistemas fluido-sólido.
La trasferencia de materia de la fase gaseosa a la líquida y a la inversa, puede
producirse por burbujeo del gas en el seno del líquido o bien utilizando torres de paredes mojadas,
rellenas con cilindros, esferas sencillas o partículas de cualquier forma.
Capítulo 7 - Reacciones Heterogéneas
3
________________________________________________________________________________________________________
Recordemos que la teoría de la doble capa establece que en la interface de ambos
fluidos se forma una doble capa estacionaria, una para cada fluido, donde se concentra la
resistencia a la transferencia de materia.
En la Fig. 7.1.- se muestra gráficamente acerca de la teoría de la capa límite.
Interface
Fase Gaseosa
Capa estacionaria
Gaseosa
Capa estacionaria
líquida
Fase Líquida
Fig. 7.1.-
pG
CG
pi
Ci
pL
CL
Donde:
pG : presión parcial del gas que difunde en la fase gaseosa.
pi : presión parcial del gas en la interface.
pL : presión parcial del gas de concentración CL.
CG : concentración del componente que difunde en la fase gaseosa.
Ci : concentración en la interface.
CL : concentración del componente que difunde en la capa líquida.
La velocidad de transporte de materia a través de cualquiera de estas capas varía
proporcionalmente con el área de intercambio, con el potencial de difusión y con el gradiente de
concentraciones o presiones parciales, y en forma inversamente proporcional al espesor de las
capas estacionarias, el que normalmente está englobado en la constante de proporcionalidad.
La expresión de la velocidad será entonces una de las siguientes expresiones:
rd = kG S (pG - pi)
7.1.-
rd = kL S ( Ci – CL)
7.2.-
rd = k0G S (pG – pL)
7.3.-
rd = k0L S (CG – CL)
7.4.-
Los factores k son coeficientes de transporte de materia, y dependen de las propiedades
geométricas y físicas del sistema.
Estos factores están relacionados por los siguientes números adimensionales:
Número de Reynolds = Re = d v /
7.5.-
Número de Schmidt = Sc = /Dv
7.6.-
Capítulo 7 - Reacciones Heterogéneas
4
________________________________________________________________________________________________________
Número de Sherwood = Sh = k d M/Dv
7.7.-
Donde:
d = diámetro de partículas de relleno o de tubo para paredes mojadas.
v = velocidad lineal del fluido.
 = densidad del fluido.
 = viscosidad del fluido.
Dv = difusividad [m2/h]
M = peso molecular.
kG = coeficiente de trasporte de materia [mol/h m2 atm.] a través de la fase gaseosa.
kL = coeficiente de trasporte de materia [mol/h m2 unidad de concentrac.] a través de la fase
líquida.
k0G = coeficiente global de trasporte de materia para las diferencias de presiones parciales.
k0L = coeficiente global de trasporte de materia para las diferencias de concentraciones.
S = superficie de intercambio en la interface.
Para el cálculo de los coeficientes k se han desarrollado ecuaciones empíricas tales
como la de Gilliland y Sherwood para el caso de tubos de pared mojada:
K d M/ Dv = 0,23 (Re) 0,81 (Sc) 0,44
7.8.-
Mientras que para torres de relleno se puede aplicar las ecuaciones de Hobson y Thodos:
log jd = 0,7683 – 0,9175 log Re + 0,0817 (log Re)2
7.9.-
En la cual:
jd = (k CM/LM) (Sc)2/3
7.10.-
Para líquidos, y:
jd = (k pM/GM) (Sc)2/3
Para gases, donde:
7.11.-
Capítulo 7 - Reacciones Heterogéneas
5
________________________________________________________________________________________________________
CM = concentración media del comp. que no difunde en la fase líquida.
pM = presión parcial media del comp..que no difunde en la fase.
LM = velocidad másica molar [mol/h m2 sección transversal] de la fase líq.
GM = velocidad másica molar [mol/h m2 sección transversal] de la fase gas.
Las ecuaciones 7.8.- y 7.10.- son aplicables cuando la resistencia a la difusión es muy
diferente entre ambas capas, es decir cuando una de ellas es despreciable frente a la otra, y
sirven para determinar kG o kL, las concentraciones o presiones que correspondan a la fase con
mayor resistencia.
Cuando las resistencias a la transferencia de materia son comparables en ambas fases,
se calculan los coeficientes globales k0G o k0L, los cuales engloban a los coeficientes individuales.
Por ejemplo, si la solubilidad del gas se ajusta a la ley de Henry, es decir p=h C:
𝟏
𝒌𝑶𝑮
𝟏
𝒌𝑶𝑳
=
=
𝟏
𝒌𝑮
𝟏
𝒌𝑳
+
+
𝑯
𝒌𝑳
𝟏
𝑯𝒌𝑮
7.12
7-13
Para las reacciones donde solo existen las fases sólida y líquida, la ecuación que define
la velocidad de transporte de materia desde la fase gaseosa hasta la superficie del sólido es:
𝒓𝒅 = 𝒌𝒅𝒊𝒇 (𝒑𝒈 − 𝒑𝒊 )
7.14.-
La última ecuación es válida tanto para las reacciones catalíticas como para las no
catalíticas.
7.2.1.2.- Velocidad de Adsorción de los Reactivos.
La forma de la ecuación de velocidad tomará distintas formas, según sea el tipo de
reacción de que se trate:
1.- Sea una reacción del tipo:
A B
donde se supone el siguiente mecanismo:
A + X  AX  B + X
siendo X el sitio activo.
Capítulo 7 - Reacciones Heterogéneas
6
________________________________________________________________________________________________________
Recordemos que las ecuaciones 6.7.-, 6.8.-, 6.10.- y 6.11.- de acuerdo con la teoría de la
adsorción de Langmuir, expresaban las velocidades de adsorción y desorción en función de los
espacios vacíos, de las concentraciones y de las presiones de reactivo:
𝒓𝒂 = 𝒌𝒂𝒅 𝒑 (𝟏 − 𝜽)
6.7.-
𝒓𝒅 = 𝒌′𝒅𝒆𝒔 𝜽
6.8.-
𝒓𝒂 = 𝒌𝒂𝒅 𝑪𝒈 (𝑪𝒎 − 𝑪)
6.10.-
𝒓𝒅 = 𝒌′𝒅𝒆𝒔 𝑪
6.11.-
donde:
C = concentración adsorbida C en el catalizador expresada en moles de gas adsorbido por gramo
de catalizador.
Cm = concentración en moles de una capa monomolecular completa sobre la superficie del
catalizador.
Cg = concentración del reactivo en la fase gaseosa.
p = presión parcial del reactivo.
En la 6.10.-, el término:
(𝑪𝒎 − 𝑪) = 𝑪𝑽
7.15.-
representa la concentración de centros vacíos.
Es evidente que la velocidad neta de adsorción será la diferencia entre las 6.10.- y 6.11.-
𝒓𝒂𝒅 = 𝒓𝒂 − 𝒓𝒅 = 𝒌𝒂𝒅 𝑪𝒈 (𝑪𝒎 − 𝑪) − 𝒌𝒅𝒆𝒔 𝑪 = 𝒌𝒂𝒅 𝑪𝒈 𝑪𝑽 − 𝒌′𝒅𝒆𝒔 𝑪
𝒓𝒂𝒅 = 𝒌𝒂𝒅 (𝑪𝒈 𝑪𝑽 − 𝑪⁄𝑲 )
𝒂𝒅
7.16.-
Si expresamos esta velocidad en términos de concentraciones para una especie A:
𝒓𝒂𝒅 = 𝒌𝒂𝒅 𝑪𝑨 (𝑪𝒎 − 𝑪) − 𝒌′𝒂𝒅 𝑪𝑨(𝒂𝒅)
7.17.-
𝒓𝒂𝒅 = 𝒌𝒂𝒅 𝑪𝑨 𝑪𝑽 − 𝒌′𝒂𝒅 𝑪𝑨(𝒂𝒅)
7.18.-
2.- Reacción del tipo:
A2  2 A
A2 + 2X  2 AX  Producto + 2X
Capítulo 7 - Reacciones Heterogéneas
7
________________________________________________________________________________________________________
es decir, se trata de una molécula diatómica que se disocia en la superficie, ocupando dos sitios
activos.
Como cada una de las moléculas disociadas ocupa una fracción de superficie no
cubierta, la velocidad de adsorción será:
𝒓𝒂𝒅 = 𝒌𝒂𝒅 𝒑 (𝟏 − 𝜽)
7.19.-
mientras que la velocidad de desorción se expresará como:
𝒓𝒅𝒆𝒔 = 𝒌𝒅𝒆𝒔 𝜽𝟐
7.20.-
y, en el equilibrio:
𝜽=
𝑲½ 𝒑 ½
7.21.-
𝟏+𝑲½ 𝒑½
A + B  Producto
3.- Reacción del tipo:
A + B + 2X  AX + BX  Producto + 2X
donde las dos moléculas se adsorben.
Si llamamos:
𝜽𝑨 = Fracción de superficie ocupada por A.
𝜽𝑩 = Fracción de superficie ocupada por B.
Se deberán plantear dos ecuaciones de velocidad, una para cada componente, ya que es
muy poco probable que el catalizador tenga igual selectividad para ambos reactivos:
𝒓𝑨(𝒂𝒅) = 𝒌𝑨(𝒂𝒅) 𝒑𝑨 (𝟏 − 𝜽𝑨 − 𝜽𝑩 )
7.22.-
𝒓𝑩(𝒂𝒅) = 𝒌𝑩(𝒂𝒅) 𝒑𝑩 (𝟏 − 𝜽𝑨 − 𝜽𝑩 )
7.23.-
para las velocidades de adsorción de A y B respectivamente, y:
𝒓𝑨(𝒅𝒆𝒔) = 𝒌𝑨(𝒅𝒆𝒔) 𝜽𝑨
7.24.-
𝒓𝑩(𝒅𝒆𝒔) = 𝒌𝑩(𝒅𝒆𝒔) 𝜽𝑩
7.25.-
para la desorción.
En el equilibrio:
𝜽𝑨 = 𝑲𝑨
𝒑𝑨
𝟏+𝑲𝑨 𝒑𝑨 +𝑲𝑩 𝒑𝑩
7.26-
Capítulo 7 - Reacciones Heterogéneas
8
________________________________________________________________________________________________________
𝜽𝑩 =
𝑲𝑩 𝒑𝑩
7.27.-
𝟏+𝑲𝑨 𝒑𝑨 +𝑲𝑩 𝒑𝑩
4.- Reacción del tipo:
A+BC
en la cual se adsorben ambos reactivos, pero uno de ellos se disocia después de ser adsorbido...
Supongamos que sea el reactivo B el que se disocia. En este caso, las velocidades de
adsorción y desorción de este reactivo serán:
𝒓𝑩(𝒂𝒅) = 𝒌𝑩(𝒂𝒅) 𝒑𝑩 (𝟏 − 𝜽𝑨 − 𝜽𝑩 )𝟐
7.28.-
𝒓𝑩(𝒅𝒆𝒔) = 𝒌𝑩(𝒅𝒆𝒔) (𝜽𝑩 )𝟐
7.29.-
y la superficie ocupada por cada uno de los reactivos será:
𝜽𝑨 = [𝟏+𝑲
𝑲𝑨 𝒑 𝑨
𝑨 𝒑𝑨 +(𝑲𝑩 𝒑𝑩 )
𝜽𝑩 = [𝟏+𝑲
½]
(𝑲𝑩 𝒑𝑩 )½
𝑨 𝒑𝑨 +(𝑲𝑩 𝒑𝑩 )
½]
7.30.-
7.30.-
7.2.1.3.- Velocidad de Reacción de Superficie.
Se pueden presentar varios casos, según el tipo de reacción de que se trate:
a.- Reacción tipo A  B.
Es el caso más simple, ya que si se supone un mecanismo como el siguiente:
A + X  AX  B
La velocidad de reacción será proporcional a la fracción superficie cubierta por el reactivo
A:
𝒓𝒒 = 𝒌𝒒 𝜽𝑨
7.31.-
b.- Reacción del tipo A  B.
En este caso, la reacción directa será:
𝒓𝒒𝒅 = 𝒌𝒒 𝜽𝑨
7.32.-
y la reacción inversa será proporcional a la superficie cubierta por el producto que no ha sido
desorbido:
Capítulo 7 - Reacciones Heterogéneas
9
________________________________________________________________________________________________________
𝒓𝒒𝒊 = 𝒌′𝒒 𝜽𝑩
7.33.-
La velocidad neta será:
𝒓𝒒 = 𝒓𝒒𝒅 − 𝒓𝒒𝒊 = 𝒌𝒒 𝜽𝑨 − 𝒌′𝒒 𝜽𝑩
7.34.-
c.- Reacción tipo A(ad) + B  C.
En este caso, la reacción se produce entre una molécula de A adsorbida y una de B no
adsorbido.
La expresión de la velocidad será:
𝒓𝒒 = 𝒌𝒒 𝑪𝑨(𝒂𝒅) 𝑪𝑩 − 𝒌′𝒒 𝑪𝑪(𝒂𝒅)
7.35.-
d.- Reacción tipo A(ad) + B(ad)  C.
El mecanismo que se supone es:
AX + BX  CX + X
En este caso, solamente reaccionarán aquellas moléculas de A y B que estén adsorbidas
en centros adyacentes. Como resulta imposible conocer si una molécula de A adsorbida ocupa un
centro inmediatamente adyacente a uno que donde se adsorbió uno de B, se asume que esta
situación efectivamente ocurre.
Por lo tanto, la velocidad de reacción directa será proporcional a la concentración de A
adsorbido y a la fracción de superficie total ocupada por B adsorbido. Si se denomina θB=CB(ad)/Cm
donde Cm es la concentración molar total de centros:
𝒓𝒒𝒅 = 𝒌𝒒 𝑪𝑨(𝒂𝒅) 𝜽𝑩 =
𝒌𝒒 𝑪𝑨(𝒂𝒅) 𝑪𝑩(𝒂𝒅)
𝑪𝒎
7.36.-
Por su parte, la reacción inversa será proporcional a la concentración de producto no
desorbido y a la concentración de centros vacíos adyacentes a CC(ad), por lo tanto:
𝒓𝒒𝒊 =
𝒌′ 𝒒 𝑪𝑪(𝒂𝒅) 𝑪𝑽
𝑪𝒎
7.37.-
y la velocidad neta será:
𝟏
𝒓𝒒 = (𝑪 )[(𝒌𝒒 𝑪𝑨(𝒂𝒅) 𝑪𝑩(𝒂𝒅) ) − (𝒌′𝒒 𝑪𝑪(𝒂𝒅) 𝑪𝑽 )]
𝒎
7.2.1.4.- Velocidad de Desorción de los Productos.
Este mecanismo puede representarse por la siguiente reacción química:
CX  C + X
7.38.-
Capítulo 7 - Reacciones Heterogéneas
10
________________________________________________________________________________________________________
La reacción directa será proporcional a la concentración de C adsorbido, mientras que la
inversa será proporcional a la concentración de C no adsorbido y la concentración de sitios vacíos.
Por lo tanto:
𝒓𝒅 = 𝒌𝒅 𝑪𝑪(𝒂𝒅) − 𝒌′𝒅 𝑪𝑪 𝑪𝑽
7.39.-
7.3.- Etapa Dominante o Controlante de la Velocidad.
En las ecuaciones anteriores, las concentraciones adsorbidas, tales como CA(ad), CB(ad),
CC(ad), Cv, etc., no son las formas más prácticas de expresar las cantidades de materia que
intervienen en la reacción, ya que éstas son de difícil medición.
Adicionalmente, en todas éstas expresiones figuran las constantes específicas de
velocidad ki, las que obviamente están expresadas en términos de concentraciones de reactivos
adsorbidos, lo que dificulta aún más la resolución de las mismas.
Por ello, es conveniente expresar las velocidades en función de las concentraciones en
el fluido y de las constantes de equilibrio.
En los fenómenos de superficie, cuyas concentraciones no son fáciles de medir, en el
estado estacionario tanto la velocidad de reacción de superficie como las de adsorción y desorción
serán iguales. Pero indudablemente será muy raro que fuera de este estado particular tengan
iguales valores. Normalmente una de ellas será más lenta que las otras, y en este caso se
cumplirá que esa será la etapa dominante o etapa controlante del proceso.
Supongamos la siguiente reacción:
A+BC
que responde al siguiente mecanismo:
A + X  AX
B + X  BX
AX + BX  CX + X
CX  C + X
_________________
A+BC
7.3.1.- Reacción de Superficie Controlante
Recordemos que la 7.18.- nos da la velocidad de reacción para una reacción del tipo:
A  B:
𝒓𝒒 = 𝒌𝒒 𝑪𝑨 𝑪𝑽 − 𝒌′𝒒 𝑪𝑨(𝒂𝒅)
En el equilibrio, 𝒓𝒒 será igual a cero:
7.18.-
Capítulo 7 - Reacciones Heterogéneas
11
________________________________________________________________________________________________________
𝒌𝒒 𝑪𝑨 𝑪𝑽 = 𝒌′𝒒 𝑪𝑨(𝒂𝒅)
7.40.-
Indudablemente se puede definir una constante de equilibrio, y adoptaremos como valor
de la misma el cociente de las constantes específicas de velocidad, aunque debemos tener
presente que puede no ser el valor correcto:
𝑲𝑨 = 𝒌𝒒 ⁄𝒌′ 𝒒 = 𝑪𝑨(𝒆𝒒) ⁄𝑪𝑨 𝑪𝑽
7.41.-
y
𝑪𝑨(𝒆𝒒) = 𝑲𝑨 𝑪𝑨 𝑪𝑽
7.42.-
donde 𝑲𝑨 es la constante de equilibrio de adsorción de la especie A.
En el caso de la reacción en estudio se deberá determinar una constante de equilibrio de
adsorción para cada especie reaccionante, porque como ya se mencionó cada catalizador tiene
una especificidad diferente para cada especie.
Por analogía:
𝑲𝑩 = 𝑪𝑩(𝒆𝒒) ⁄𝑪𝑩 𝑪𝑽
7.43.-
𝑲𝑪 = 𝑪𝑪(𝒆𝒒) ⁄𝑪𝑪 𝑪𝑽
7.44.-
𝑪𝑩(𝒆𝒒) = 𝑲𝑩 𝑪𝑩 𝑪𝑽
7.45.-
𝑪𝑪(𝒆𝒒) = 𝑲𝑪 𝑪𝑪 𝑪𝑽
7.46.-
y
Modificando la 7.38.-, que es la ecuación que define el valor de la velocidad de reacción
superficial para la reacción propuesta:
𝒓𝒒 = (𝒌𝒒 ⁄𝑪𝒎 )[(𝑪𝑨(𝒂𝒅) 𝑪𝑩(𝒂𝒅) ) − (𝑪𝑪(𝒂𝒅) 𝑪𝑽 ⁄𝑲𝒒 )]
7.47.-
En el equilibrio será rq = 0, por lo tanto, como en el caso anterior se asume que:
𝑲𝒒 = 𝑪𝑪(𝒂𝒅) 𝑪𝑽 /𝑪𝑨(𝒂𝒅) 𝑪𝑩(𝒂𝒅)
7.48.-
Por lo tanto la 7.47.- puede expresarse como:
𝒓 = (𝒌𝒒 ⁄𝑪𝒎 ) (𝑲𝑨 𝑲𝑩 𝑪𝑨 𝑪𝑩 𝑪𝟐𝑽 − 𝑲𝑪 𝑪𝟐𝑽 )
7.49.-
La concentración total de centros es:
𝑪𝒎 = 𝑪𝑽 + 𝑪𝑨(𝒂𝒅) + 𝑪𝑩(𝒂𝒅) + 𝑪𝑪(𝒂𝒅)
7.50.-
como CA(ad), CB(ad) y CC(ad) corresponden a los valores de equilibrio de la adsorción, se pueden
combinar las 7.42.-, 7.43.- y 7.44.- con la 7.50.-:
Capítulo 7 - Reacciones Heterogéneas
12
________________________________________________________________________________________________________
𝑪𝑽 = 𝑪𝒎 /(𝟏 + 𝑲𝑨 𝑪𝑨 + 𝑲𝑩 𝑪𝑩 + 𝑲𝑪 𝑪𝑪 )
7.51.-
Combinando la 7.49.- con las anteriores:
𝒓 = 𝒌𝒒 𝑪𝒎 [𝑲𝑨 𝑲𝑩 𝑪𝑨 𝑪𝑩 − (𝑲𝑪 ⁄𝑲𝒒 )𝑪𝑪 ]/(𝟏 + 𝑲𝑨 𝑪𝑨 + 𝑲𝑩 𝑪𝑩 + 𝑲𝑪 𝑪𝑪 )𝟐
7.52.-
Recordemos que la constante de equilibrio para la reacción no catalizada, es decir la
reacción común valía:
𝑲 = (𝑪𝑪 ⁄𝑪𝑨 𝑪𝑩 )𝒆𝒒
7.53.-
y que puede relacionarse con las constantes de equilibrio de adsorción mediante la 7.42.-, 7.43.-,
7.44.- y 7.48.-:
𝑲 = (𝑪𝑪(𝒂𝒅) /𝑲𝑪 𝑪𝑽 )/(𝑪𝑨(𝒂𝒅) /𝑲𝑨 𝑪𝑽 )(𝑪𝑩(𝒂𝒅) /𝑲𝑩 𝑪𝑽 ) =
= (𝑲𝑨 𝑲𝑩 /𝑲𝑪 )(𝑪𝑪(𝒂𝒅) 𝑪𝑽 /𝑪𝑨 𝑪𝑩 ) = (𝑲𝑨 𝑲𝑩 /𝑲𝑪 )𝑲𝒒
7.54.-
Reemplazando este valor en la 7.52.-:
𝒓 = 𝒌𝒒 𝑪𝒎 𝑲𝑨 𝑲𝑩 (𝑪𝑨 𝑪𝑩 − (𝟏/𝑲)𝑪𝑪 )/(𝟏 + 𝑲𝑨 𝑪𝑨 + 𝑲𝑩 𝑪𝑩 + 𝑲𝑪 𝑪𝑪 )𝟐
7.55.-
Recordemos que este resultado sólo es válido para:
a) Cuando la reacción de superficie es controlante.
b) Se trata de una reacción tipo A + B  C.
c) Se supone una adsorción según la teoría de Langmuir.
Se pueden hacer algunas simplificaciones para casos especiales, tales como cuando la
adsorción es débil para todos los componentes. En este caso, el denominador de la 7.55.- tiende
a 1, y en consecuencia:
𝟏
𝒓 = 𝒌𝒒 𝑪𝒎 𝑲𝑨 𝑲𝑩 [𝑪𝑨 𝑪𝑩 − (𝑲) 𝑪𝑪 ]
7.56.-
En el caso que el producto sea fuertemente adsorbido, el producto CCKC resultará mucho
mayor que los otros términos del denominador, y se puede escribir:
𝒓=
𝒌𝒒 𝑪𝒎 𝑲𝑨 𝑲𝑩 𝑪𝑨 𝑪𝑩
(𝑲𝑪 𝑪𝑪 )𝟐
7.57.-
Cuando se produce una reacción del tipo A  B, es decir que hay un solo reactivo, la
ecuación toma la siguiente forma:
𝒓=
𝒌𝒒 𝑪𝒎 𝑲𝑨 𝑪𝑨
𝑲𝑪 𝑪𝑪
7.58.-
Capítulo 7 - Reacciones Heterogéneas
13
________________________________________________________________________________________________________
7.3.2.- Adsorción o Desorción Controlante.
Se supone que la reacción es del tipo:
A+BC
Si la velocidad de adsorción de A es lenta, ésta será la etapa controlante del proceso, y
está representada por la 7.18.-
𝒓𝒂𝒅 = 𝒌𝒂𝒅 𝑪𝑨 𝑪𝑽 − 𝒌′𝒂𝒅 𝑪𝑨(𝒂𝒅)
7.18.-
Por su parte, la concentración de A adsorbido será, de acuerdo a la 7.48.-:
𝑪𝑨(𝒂𝒅) = 𝑪𝑽 𝑪𝑪 /𝑲𝒒 𝑪𝑩 = 𝑪𝑽 (𝑲𝑪 𝑪𝑪 𝑪𝑽 )/𝑲𝒒 (𝑲𝑩 𝑪𝑩 𝑪𝑽 ) = 𝑪𝑽 𝑲𝑪 𝑪𝑪 /𝑲𝒒 𝑲𝑩 𝑪𝑩
7.59.-
Por la 7.54.- la expresión de CA(ad) puede simplificarse aún más:
𝑪_𝑨(𝒂𝒅) = (𝑲_𝑨 𝑪_𝑽 𝑪_𝑪)/(𝑲𝑪_𝑩 )
7.60.-
Sustituyendo estos valores en la 7.18.-:
𝒓 = 𝒌𝒂𝒅 𝑪𝑽 (𝑪𝑨 − (𝑪𝑪 ⁄𝑲𝑪𝑩 ))
7.61.-
Si el valor de Cv se expresa en función de las ecuaciones 7.50.-, de los valores de CB(ad)
y CC(ad) que surgen de las 7.45.- y 7.46.- y el valor de CA(ad) de la 7.59.- y se reemplazan en la
7.60.- :
𝒓=
𝟏 𝑪
𝒌𝒂𝒅 𝑪𝒎 [𝑪𝑨 −( )( 𝑪 )]
𝑲 𝑪𝑩
𝑲𝑨 𝑪𝑪
[𝟏+𝑲𝑩 𝑪𝑩 +( )( )+𝑲𝑪 𝑪𝑪 ]
𝑲
𝑪𝑩
7.62.-
Si es la desorción del producto C la etapa lenta del proceso, la forma de la velocidad
estará dada por la ecuación
𝑪𝑪(𝒂𝒅)
𝟏
𝒓 = (𝑪 ) [𝒌𝒅 𝑪𝑨(𝒂𝒅) 𝑪𝑩(𝒂𝒅) ) − (𝒌′ 𝒅 𝑪𝑪(𝒂𝒅) 𝑪𝑽 ] = −𝒌𝒅 [𝑪𝑪 𝑪𝑽 − (
𝒎
𝑲𝑪
)]
7.63.-
es decir, la 7.38.- modificada. Si se efectúan los reemplazos correspondientes el valor de la
velocidad será:
𝑪
𝒌𝒅 𝑪𝒎 𝑲[𝑪𝑨 𝑪𝑩 −( 𝑪 )]
𝒓 = (𝟏+𝑲
𝑲
𝑨 𝑪𝑨 +𝑲𝑩 𝑪𝑩 +𝑲𝑪 𝑲𝑪𝑨 𝑪𝑩 )
7.64.-