Exámenes Ingeniería Técnica Industrial. Mecánica X

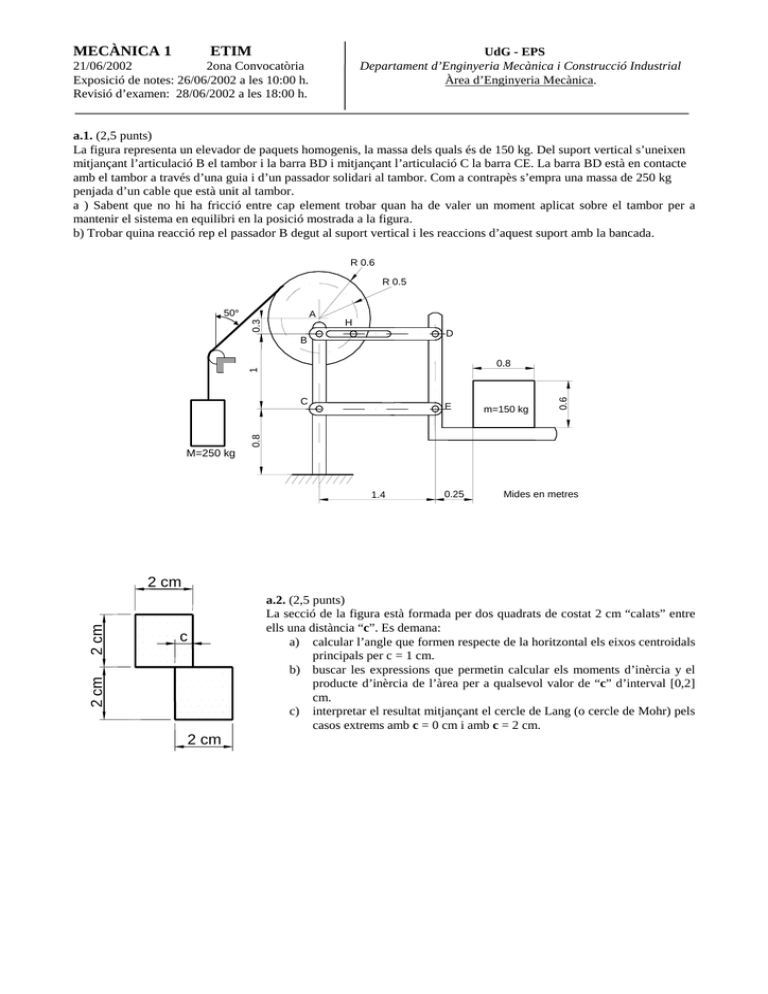
MECÀNICA 1
ETIM
UdG - EPS
Departament d’Enginyeria Mecànica i Construcció Industrial
Àrea d’Enginyeria Mecànica.
21/06/2002
2ona Convocatòria
Exposició de notes: 26/06/2002 a les 10:00 h.
Revisió d’examen: 28/06/2002 a les 18:00 h.
a.1. (2,5 punts)
La figura representa un elevador de paquets homogenis, la massa dels quals és de 150 kg. Del suport vertical s’uneixen
mitjançant l’articulació B el tambor i la barra BD i mitjançant l’articulació C la barra CE. La barra BD està en contacte
amb el tambor a través d’una guia i d’un passador solidari al tambor. Com a contrapès s’empra una massa de 250 kg
penjada d’un cable que està unit al tambor.
a ) Sabent que no hi ha fricció entre cap element trobar quan ha de valer un moment aplicat sobre el tambor per a
mantenir el sistema en equilibri en la posició mostrada a la figura.
b) Trobar quina reacció rep el passador B degut al suport vertical i les reaccions d’aquest suport amb la bancada.
R 0.6
R 0.5
50°
A
0.3
H
D
B
C
m=150 kg
0.8
E
0.6
1
0.8
M=250 kg
1.4
0.25
Mides en metres
c
2 cm
2 cm
2 cm
2 cm
a.2. (2,5 punts)
La secció de la figura està formada per dos quadrats de costat 2 cm “calats” entre
ells una distància “c”. Es demana:
a) calcular l’angle que formen respecte de la horitzontal els eixos centroidals
principals per c = 1 cm.
b) buscar les expressions que permetin calcular els moments d’inèrcia y el
producte d’inèrcia de l’àrea per a qualsevol valor de “c” d’interval [0,2]
cm.
c) interpretar el resultat mitjançant el cercle de Lang (o cercle de Mohr) pels
casos extrems amb c = 0 cm i amb c = 2 cm.
MECÀNICA 1
ETIM
21/06/2002
2ona Convocatòria
Exposició de notes: 26/06/2002 a les 10:00 h.
Revisió d’examen: 28/06/2002 a les 18:00 h.
UdG - EPS
Departament d’Enginyeria Mecànica i Construcció Industrial
Àrea d’Enginyeria Mecànica.
b.1. (2 punts)
g = 10 m/s2
A
G
A
O
B
B
50 mm
50 mm
50 mm
La barra homogenea de gruix menyspreable i amb 10 Kp de pes amb centre de gravetat al punt G es recolza a les
espigues A i B. Les espigues A i B són solidàries al disc que pot girar al voltant del seu centre (el punt 0). Calcular:
a)
La reacció en A per un angle de rotació de 20º en sentit horari considerant coeficient de frec entre la barra i la
espiga A de 0,5, en aquest cas que no hi ha fricció a l’espiga B (coeficient de fricció és zero a B).
b) L’àngle de rotació, en sentit horari, que pot girar el disc sense produir moviment relatiu barra-disc si el
coeficient de frec entre la barra i les dues espigues (A i B) val 0,5
c) L’angle de rotació, en sentit antihorari, que pot girar el disc sense produir moviment relatiu barra-disc si el
coeficient de frec entre la barra i les dues espigues (A i B) val 0,5
k
B
b
A
F
b.2. (1,5 punts)
Cada molla del mecanisme representat a la figura té una constant de rigidesa k i està
distesa quan la cota L val zero. Cada barra, de pes menyspreable, té una longitud b.
Estan articulades entre elles en el punt A. La barra superior està guiada verticalment
en el punt B i la barra inferior en el punt C.
Calcular mitjançant el mètode de treball virtual la força F necessària per originar un
desplaçament L del punt A (indicar el resultat en funció de k, b i L)
b
C
k
e
L
b.3. (1,5 punts)
A l’aplicar un pes Ps de 100 N al voltant de la politja de
diàmetre 25 mm el tambor de diàmetre 88 mm i de 500
N de pes es manté en equilibri mitjançant un fre de cinta
amb coeficient de fricció µe = 0,8 accionat per un
cilindre hidràulic. Si l’angle abraçat per la cinta és de
180º i considerant que totes les altres forces de fricció i
les altres masses dels sòlids són negligibles es demana :
g
f
C
h
D
Ps
P
A
B
a) La pressió mínima d’alimentació del cilindre hidràulic necessària per mantenir el tambor en equilibri.
b) La tensió que experimenta la barra DB, considerant que la secció de totes les barres és de 100 mm2.
Mides: CD = 138 mm ; ef = 25 mm ; fg = 88 mm ; gh = 50 mm
Dades cilindre hidràulic : diàmetre tija 20 mm, diàmetre pistó 100 mm