Exámen Ingeniería Industrial. Mecánica II
Anuncio

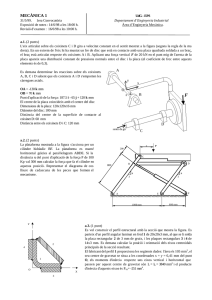
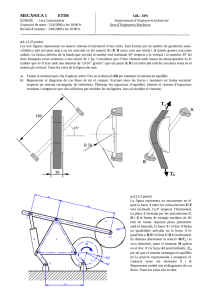
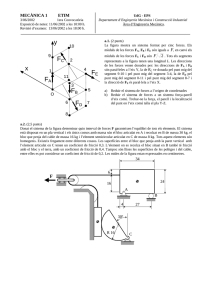
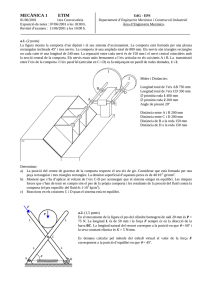
MECÀNICA 1 UdG - EPS Departament d’Enginyeria Industrial Àrea d’Enginyeria Mecànica. 7/7/98. 2ona Convocatòria Exposició de notes : 17/7/98 a les 18:00 h. Revisió d’examen : 20/7/98 a les 9:00 h. a.1. ( 2 punts) Una grua de braç telescòpic quan es col·loca en posició de treball es recolza sobre tres peus hidràulics. Té una articulació que permet girar la torreta 360º sobre el pla horitzontal i una altra que permet variar la inclinació del braç (? ). La posició del seu centre de masses (cdm), dels recolzaments amb el terra i de les mides importants es poden trobar en les dues figures de l’esquerra (alçat i perfil). La longitud màxima L que pot assolir el braç telescòpic és de 7 metres. La grua té una massa de 30 tones i el braç està dissenyat per suportar una càrrega màxima P de 14 tones. Si la grua està sobre una superfície horitzontal i la torreta està en la posició que marca el dibuix en planta de la dreta, trobeu l’angle ? mínim que pot inclinar-se el braç que garanteixi que la grua mai bolqui. (El centre de coordenades x-y proposat està situat sobre l’eix de gir de la torreta) A P y P ? cdm x cdm C B C B E G H D A B A B A C a.2.. (2 punts) En el mecanisme situat sobre el pla vertical de la figura els punts A, B i C són punts fixes alineats sobre una bancada. L’únic element que té massa és el EGH el seu centre de gravetat és el punt G i pesa 10 N. Si no existeix fricció entre cap dels elements del mecanisme determinar: a) la tensió del cable DH per aconseguir que el mecanisme estigui en equilibri en la posició mostrada, b) la força a que està sotmesa la barra BE a.3. (1,5 punt) Tenim una secció com la mostrada a la figura. Determinar la posició i orientació dels eixos centroidals principals de la secció. MECÀNICA 1 UdG - EPS Departament d’Enginyeria Industrial Àrea d’Enginyeria Mecànica. 7/7/98. 2ona Convocatòria Exposició de notes : 17/7/98 a les 18:00 h. Revisió d’examen : 20/7/98 a les 9:00 h. b.1. (2 punts) La barra AC homogènia de pes 50 Kp i longitud d=400 mm és estirada pel punt A i es mou cap a l’esquerra. El coeficient de fricció dinàmic de la barra en A i en B és ?=0,5. a) Trobar quin és el mínim valor del pes del bloc de base b=60 mm per evitar que bolqui si l’angle entre barra i terra val ? =20º b) Amb el valor del pes trobat a l’anterior apartat, determina el mínim coeficient de fricció estàtic entre el bloc i el pla necessari per evitar el lliscament del bloc C B ? A A W B F b.2. (1’5 punts) L’esquema representa l’alçat d’una porta de garatge de dues fulles articulades per una frontis sa a B. Les dues peces de la porta amb massa apreciable són: la fulla AB de 100 Kg i la BC de 120 Kg. Els seus centres de masses estan en el seu centre geomètric. L’articulació A és fixa, mentre que el punt C és un passador que es mou per una guia vertical (la guia que va des del terra fins a A). Sobre C hi tenim lligat un contrapès W de 110 Kg. Determinar emprant el mètode de treball virtual quina força F (sempre perpendicular a la línia BC) es necessita per mantenir la porta en equilibri en funció de l’angle de les fulles respecte el pla vertical. C b.3. Pràctiques (1 punt, 10% de la nota) Tenim una estructura (mirar figura) de barres articulades d’acer totes elles de la mateixa longitud i amb la mateixa secció transversal. La barra que uneix els nusos 2 i 5 té col·locada una galga extensiomètrica que mesura les deformacions longitudinals. Determinar la força vertical P, si amb aquesta força la galga ens dóna un valor de -75·10-6m/m. (mòdul elàstic de l’acer 210 000 N/mm2, àrea de les seccions de les barres 20 mm2.) 2 1 3 5 4 P