Exámenes Ingeniería Técnica Industrial. Mecánica V
Anuncio
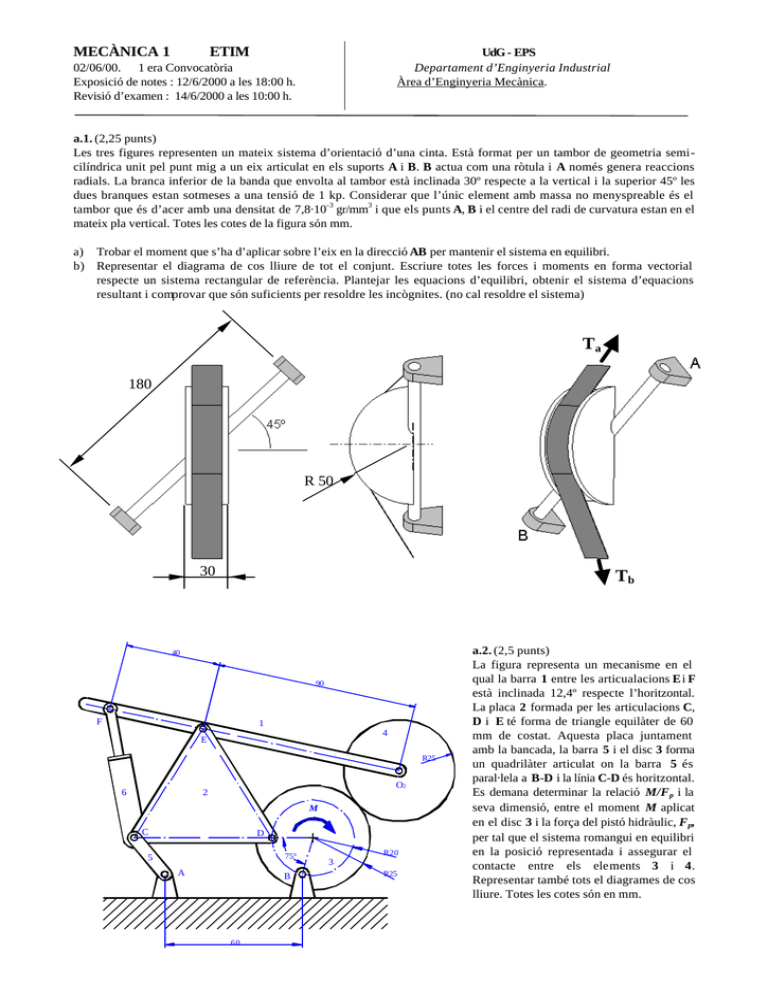
MECÀNICA 1 ETIM UdG - EPS Departament d’Enginyeria Industrial Àrea d’Enginyeria Mecànica. 02/06/00. 1 era Convocatòria Exposició de notes : 12/6/2000 a les 18:00 h. Revisió d’examen : 14/6/2000 a les 10:00 h. a.1. (2,25 punts) Les tres figures representen un mateix sistema d’orientació d’una cinta. Està format per un tambor de geometria semicilíndrica unit pel punt mig a un eix articulat en els suports A i B. B actua com una ròtula i A només genera reaccions radials. La branca inferior de la banda que envolta al tambor està inclinada 30º respecte a la vertical i la superior 45º les dues branques estan sotmeses a una tensió de 1 kp. Considerar que l’únic element amb massa no menyspreable és el tambor que és d’acer amb una densitat de 7,8·10-3 gr/mm3 i que els punts A, B i el centre del radi de curvatura estan en el mateix pla vertical. Totes les cotes de la figura són mm. a) Trobar el moment que s’ha d’aplicar sobre l’eix en la direcció AB per mantenir el sistema en equilibri. b) Representar el diagrama de cos lliure de tot el conjunt. Escriure totes les forces i moments en forma vectorial respecte un sistema rectangular de referència. Plantejar les equacions d’equilibri, obtenir el sistema d’equacions resultant i comprovar que són suficients per resoldre les incògnites. (no cal resoldre el sistema) Ta 180 R 50 30 Tb 40 90 F 1 4 E R25 6 O2 2 M C D 75° 5 A B 60 R20 3 R25 a.2. (2,5 punts) La figura representa un mecanisme en el qual la barra 1 entre les articualacions E i F està inclinada 12,4º respecte l’horitzontal. La placa 2 formada per les articulacions C, D i E té forma de triangle equilàter de 60 mm de costat. Aquesta placa juntament amb la bancada, la barra 5 i el disc 3 forma un quadrilàter articulat on la barra 5 és paral·lela a B-D i la línia C-D és horitzontal. Es demana determinar la relació M/Fp i la seva dimensió, entre el moment M aplicat en el disc 3 i la força del pistó hidràulic, Fp, per tal que el sistema romangui en equilibri en la posició representada i assegurar el contacte entre els elements 3 i 4. Representar també tots el diagrames de cos lliure. Totes les cotes són en mm. MECÀNICA 1 ETIM UdG - EPS Departament d’Enginyeria Industrial Àrea d’Enginyeria Mecànica. 02/06/00. 1 era Convocatòria Exposició de notes : 12/6/2000 a les 18:00 h. Revisió d’examen : 14/6/2000 a les 10:00 h. b.1. (2,5 punts) El cilindre de la figura té una massa de 10 kg. Es recolza en les dues superfícies inclinades (ambdues a 20º respecte a la vertical) i per un element elàstic unit a B i a C. Una de les superfícies és fixa i l’altre és articulada en el punt A. Només existeix fregament entre les superfícies inclinades i el cilindre amb un coeficient de fricció 0,2. Determinar la força mínima que ha de realitzar l’element elàstic per mantenir en equilibri al cilindre en la posició mostrada. Indicar també de quina manera es mouria el cilindre si l’element BC disminuís la seva força d’aquest valor mínim. Totes les cotes de la figura són mm. B A C A b.2. (1,75 punts) El mecanisme de la figura permet el desplaçament de la càrrega W = 750 N aplicada en E. La longitud L és de 25 mm igual que el radi R, mentre que la longitud H és de 50 mm. Es demana calcular pel mètode del treball virtual la constant elàstica del ressort per garantir l’equilibri del sistema quan ? = 60º. La molla està distesa quan la barra ABC està alineada amb la cremallera i sempre roman en posició horitzontal. L B L L E C D ? W O H R MECÀNICA 1 ETIM UdG - EPS Departament d’Enginyeria Industrial Àrea d’Enginyeria Mecànica. 02/06/00. 1 era Convocatòria Exposició de notes : 12/6/2000 a les 18:00 h. Revisió d’examen : 14/6/2000 a les 10:00 h. b.3. (1,5 punts) En el muntatge de la figura, la cinta es troba recolzada sobre el tambor, subjectada en un extrem per l’estructura de barres articulades i en l’altre per un pes W. El pes P s’incrementa progressivament fins que s’aconsegueix la imminència del moviment del tambor. En aquest instant, es demana: a) Coeficient de fregament estàtic (? e ) entre el tambor i la cinta, sabent que l’angle de contacte entre la cinta i el tambor és de 90º. (0.5 p) 5 l 6 b) Força de la barra G segons el mètode dels nusos (la longitud de totes les barres horitzontals i verticals és l). Indicar també si la barra està sotmesa a tracció o compressió. (0.5 p) c) Deformació unitària (?) a la que està sotmesa la barra G, suposant que totes les barres de l’estructura són de tub quadrat d’alumini, de 20 x 20 x 1.5 mm. (0.5 p) r R l 3 4 l G P W Dades: r = 9.5 mm R = 28.5 mm P = 45 kp W = 25 kp Constant elàstica de l’alumini: E = 71.000 MPa l 1 l 2