Aplicaciones Lineales.

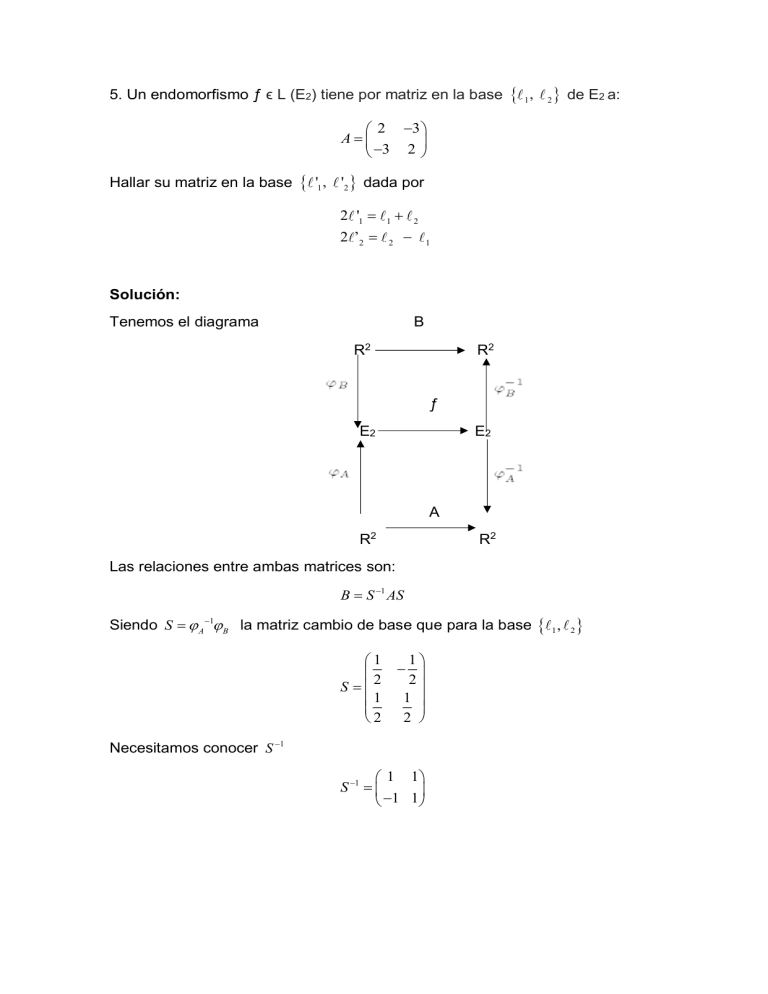
5. Un endomorfismo ƒ ϵ L (E2) tiene por matriz en la base

1
,
2

de E2 a:
 2 3 
A

 3 2 
Hallar su matriz en la base

'1 , '2  dada por
2 '1 
1
2 ’2 
2

2

1
Solución:
Tenemos el diagrama
B
R2
R2
ƒ
E2
E2
A
R2
R2
Las relaciones entre ambas matrices son:
B  S 1 AS
Siendo S   A 1 B la matriz cambio de base que para la base
1

S 2
1

2
1
 
2

1 

2 
Necesitamos conocer S 1
 1 1
S 1  

 1 1

1
,
2

y, por lo tanto
1
1
1
2

3


 2
B


 1 1 3 2   1

2
ƒ:
6. Sea
2

3
1
 
2   1 0 
 

1   0 5

2 
una aplicación lineal definida por
ƒ  x, y    2 x  y , x  y , 2 y  x 
a) Dar la matriz de ƒ en las bases naturales de 2 y 3 respectivamente;
calcular
 1
ƒ  3,  .
 2
b) Dar una base, y la dimensión de er ƒ y de Im ƒ.
c) Dar la matriz de ƒ en las bases 1 ,2  , 1 , 2 ,3  , siendo
1   2,1
2   0,3
1  1,1,1
 2   2, 0,1
3   0, 0, 2 
1
 1 
Calcular ƒ  1    2  .
 3 
2
Solución:
a) ƒ 1, 0    2,1, 1 , ƒ  0,1   1,1, 2  , luego la matriz de ƒ en las bases
naturales es
 2 1


A 1 1  y
 1 2 


b)
er ƒ   x, y  
 11 
 2 1  3   2 
7
 1 

ƒ  3,  =  1 1   1    
 
 2 
  2   2 

1
2
 2 


 
2
/ f  x, y   0 , luego
2x  y  0
 2 1 

 x 
 1 1   y   0 0 0  x  y  0
 1 2   
x  2 y  0


Sistema compatible y determinado luego
er ƒ   0, 0  y dim
er ƒ=0,
por lo tanto
dim Im ƒ=dim 2 - dim er ƒ = 2 y
Im ƒ   2,1, 1 ,  1,1, 2  
c) Tenemos el diagrama
R2
R3
R 2i 
R3i 
 2 0
Siendo S  
 la matriz de paso de la base 1 ,2  a la natural y
 1 3
1 2 0 


T  1 0 0  la matriz de paso de la base 1 , 2 ,3  a la natural. Necesitamos
1 1 2 


T 1 .
 0 4 0
1


T 1   2 2 0 
4

 1 1 2 

 3

B  T 1 AS   0
 3

 2
y, por lo tanto

3

3 
3


Finalmente, si hacemos

 3
3
 1  
f  1    2     0
 3  
2
3

 2
Observamos que
 7 

3


 2 

3
 7
 2  
13
3  
   1   1  2  3
2
4
 1
3      13 
 3    

 4
3
3
1
 1
 1
1    2   2,1   0,3   3,  ;luego
2
2
3
 3
 2
7
13
 11 7

1  2  3   , , 2 
2
4
2 2
