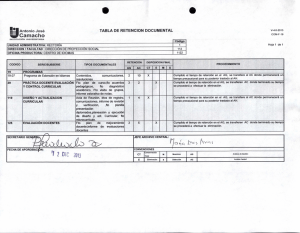
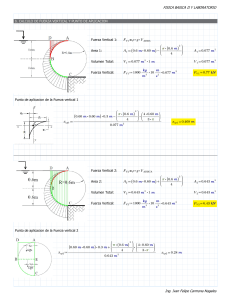
dim(U) + dim(W) ¡ dim(U \ W)

Teorema. Si V es un K-espacio vectorial ¯nitamente generado y U; W · V entonces
dim(U + W ) = dim(U) + dim(W ) ¡ dim(U \ W ):
Demostraci¶
on. Por una proposici¶on de Teor¶³a, dado que V es ¯nitamente generado, se
tiene que U + W , U, W y U \ W son ¯nitamente generados.
Sea B = fv1 ; : : : ; vr g base de U \ W . Entonces:
B es un sistema libre y B µ U luego existe B1 base de U tal que B µ B1 y entonces
B1 = fv1 ; : : : ; vr ; ur+1 ; : : : ; u sg.
B es un sistema libre y B µ W luego existe B2 base de W tal que B µ B2 y entonces
B2 = fv1 ; : : : ; vr ; wr+1 ; : : : ; wt g.
~ = B1 [ (B2 n B) = fv1 ; : : : ; vr ; ur+1 ; : : : ; us ; wr +1 ; : : : ; wt g y si probamos
Consideramos B
~ es una base de U + W se tendr¶a demostrado el Teorema.
que B
~ es sistema generador de U + W .
1. B
Si v 2 U + W entonces existen u 2 U y w 2 W tales que v = u + w.
Como u 2 U , existen ® 1 ; : : : ; ®r ; ®r+1 ; : : : ; ® s 2 K tales que u = ®1 v1 + : : : + ®r vr +
®r+1 u r+1 + : : : + ®s us .
Como w 2 U , existen ¯1 ; : : : ; ¯r ; ¯r+1 ; : : : ; ¯t 2 K tales que u = ¯1 v1 + : : : + ¯r vr +
¯r+1 w r+1 + : : : + ¯t wt .
Entonces v = u + w = ® 1 v1 + : : : + ®r vr + ® r+1 ur+1 + : : : + ®s us + ¯1 v1 + : : : + ¯r vr +
¯r+1 w r+1 + : : : + ¯t wt = (®1 + ¯1 )v1 + : : : + (®r + ¯r )vr + ® r+1 ur+1 + : : : + ® sus +
~
¯r+1 w r+1 + : : : + ¯t wt 2 hBi.
2. B es sistema libre.
1