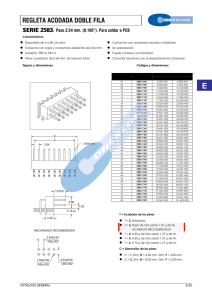
Sistema internacional (SI) de cantidades e unidades
Anuncio

Sistema internacional (SI) de cantidades e unidades
El SI es una convención:
I
Define vocabulario para propiedades físicas.
I
Propósito: Facilitar comunicación a nivel internacional.
Es un convenio internacional:
I
Institución encargada: Bureau International des Poids et
Mesures (BIPM), Francia (http://www.bipm.org)
I
Chile firmó convenio en 1908.
Sistemas alternativos/anticuados que no se deben usar:
I
MKS (metro-kilogramo-segundo): Precursor del SI.
I
CGS (centimetro-gramo-segundo): Inaceptable.
I
Unidades imperiales: Catastrófico.
Cantidades básicas, sus dimensiones e unidades
El SI define 7 cantidades básicas:
Cantidad
Largo
Masa
Tiempo
Corriente eléctrica
Temperatura termodinámica
Cantidad de sustancia
Luminosidad
Dimensión
L
M
T
I
Θ
N
J
Unidad
m
kg
s
A
K
mol
cd
Comentarios:
I
Dimension: en mayúsculo y “sans serif”.
I
Unidad: no cursiva y en minúsculo, excepto si se derivan de
apellidos de personas (Ampère, Kelvin, etc).
Hay cantidades derivadas: Fuerza, carga eléctrica, voltaje, etc.
Definición de una cantidad física
Una cantidad física tiene cierta dimensión, y se define con una
magnitud y una unidad:
Cantidad física = {Cantidad física} · [Cantidad física]
{z
} |
{z
}
|
=Magnitud
=Unidad
Análisis dimensional
Obtener la dimensión de una cantidad física:
dim (Cantidad física) = Dimensión
Ejemplo
La fuerza es una cantidad derivada. Por ejemplo F = mg, con
m = 1,5 kg y g = 9,8 m/s2 .
¿Cuál es la dimensión de la fuerza?
Solución:
dim(F ) = dim(m · g)
= dim(m) · dim(g)
= M · L · T−2
= M · L · T−2
Ejemplo
Formula del periodo de un péndulo matemático:
p
T = 2π L/g.
¡Comprueba que este periodo es un tiempo!
Solución:
1
1
dim(T ) = dim L 2 · g − 2
1
1
= (dim(L)) 2 · (dim(g))− 2
− 1
1
= L 2 · L · T−2 2
= T
Cantidades físicas adimensionales
Hay cantidades sin dimensión, pero con “unidad”.
Ejemplo
Ángulos
s
φ
φ =
R
dim(φ) =
s
R
L
=1
L
Se usan unidades para aclarar interpretación como ángulos:
I
Radian: φ = 1,5 rad
I
Grados: φ = 30◦
Análisis de unidad
Para obtener la unidad de una cantidad física:
[Cantidad física] = Unidad
Ejemplo
Período del péndulo matemático:
T = 2π
p
L/g,
con L = 1 m y g = 9,8 m/s2 .
¡Comprueba que la unidad del periodo es s (segundo)!
Solución:
1
1
[T ] = [L 2 · g − 2 ]
1
1
= [L] 2 · [g]− 2
1
= m 2 · m/s2
= s
− 12
Magnitud de una cantidad física
Para obtener la magnitud de una cantidad física:
{Cantidad física} = Magnitud
Ejemplo
L = 3,87 · 10−4 m.
¿Cuál es la magnitud de este largo?
Solución:
{L} = {3,87 · 10−4 m}
= 3,87 · 10−4
Chilenidades
Diferente de otros países latinoamericanos, en Chile se enseñó
una forma incorrecta de usar unidades.
Muchas veces se ve por ejemplo:
L = 12,56 [m]
L = 12,56 m
¡Incorrecto!
Correcto
No hay que usar el separador de miles en las ciencias. Por ejemplo:
c
= 299.792.458 m/s
c
= 299 792 458 m/s
¡Incorrecto!
Correcto
Prefijos SI
I
Se puede escribir: P = 4 538 000 W,
I
o en formato científico estándar: P = 4,538 · 107 W,
I
o usando los prefijos SI: P = 45,38 MW
Número
1012
109
106
103
10−3
10−6
10−9
10−12
10−15
Prefijo SI
T
G
M
k
m
µ
n
p
f
Nombre del prefijo
tera
giga
mega
kilo
mili
micro
nano
pico
femto
Incertidumbre en datos experimentales
Error experimental/incertidumbre se puede indicar así:
L = (4,387 ± 0,048) m
En el SI es mejor en forma compacta:
L = 4,387(48) m
Precisión de nuestro cálculo en clase
¡No hay que exagerar con el número de dígitos después del coma!
I
Sean honestos con respeto a la precisión de sus cálculos.
I
Muchas veces queremos el orden de magnitud de algo.
Ejemplo
Periodo del péndulo matemático:
T = 2π
p
L/g
con π ≈ 3,14, L = 20 cm, y g ≈ 10 m/s 2 .
¡Calcule el valor numérico del periodo del péndulo!
Solución:
r
r
√
0,2 m
2
2
T = 2 · 3,14 ·
≈ 6,3 ·
s = 6,3 ·
s
−2
s
100
10
10 m
6,3 · 1,4
≈
s ≈ 0,882 s ≈ 0,9 s
10