PRUEBAS DE HIPÓTESIS Clases de hipótesis.

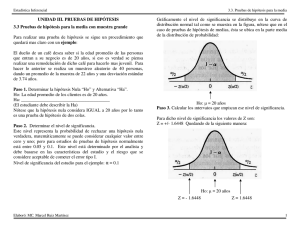
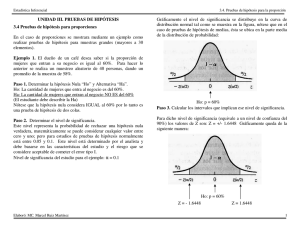
PRUEBAS DE HIPÓTESIS
Clases de hipótesis.
Una hipótesis estadística es un enunciado provisional referente a uno o más
parámetros de una población o grupo de poblaciones. En el proceso de
estadística inferencial hay dos tipos de hipótesis:
1. Hipótesis nula, designada mediante Ho y se lee .H subcero.. La letra H significa
hipótesis y el subíndice cero indica .no hay diferencia.. Por lo general en la
hipótesis nula se plantea en términos de .no hay cambio., no hay diferencia., se
plantea con el objetivo de aceptarla o rechazarla.
2. Hipótesis alternativa, describe lo que se considerará si se rechaza la
hipótesis nula. A menudo también se le denomina hipótesis de investigación, y se
designa por H1, que se lee .h subuno.
Tipos de error.
La hipótesis nula y alternativa son entonces aseveraciones sobre la población
que compiten entre sí, en el siguiente sentido: ó la hipótesis nula (Ho) es
verdadera, o lo es la hipótesis alternativa (H1), pero no ambas. En el caso ideal, el
procedimiento de prueba de hipótesis debe conducir a la aceptación de Ho cuando sea
verdadera y al rechazo de H1. Desafortunadamente no siempre es posible puesto que
como las pruebas de hipótesis se basan en la información de la muestra, se debe
considerar la posibilidad de cometer errores. La siguiente cuadro muestra los dos tipos
de errores que se pueden cometer:
Probabilidad de cometer el error tipo I
Probabilidad de rechazar Ho cuando es verdadera.
(1 - ) Probabilidad de acertar la Ho cuando es verdadera.
Probabilidad de cometer el error tipo II
Probabilidad de aceptar Ho cuando es falsa.
(1 - ) Probabilidad de rechazar Ho cuando es falsa.
Toda prueba de hipótesis determina una región de rechazo de la hipótesis llamada
región crítica, la cual depende del tipo de hipótesis que se pruebe y se
determina utilizando un nivel de significancia .
El p-valor
Es el mínimo nivel de significancia en el cual Ho sería rechazado cuando se
utiliza como procedimiento de prueba específico con un conjunto dado de
información. Si el p-valor es menor que el nivel de significancia, la hipótesis nula se
rechaza.
Pruebas para Grandes Muestras.
Este procedimiento de formulas dos hipótesis es muy similar al de un juicio en donde
se supone que el acusado es inocente hasta que se le demuestre su culpabilidad. Por
tanto se hace una hipótesis de culpabilidad cero, lo cual también ayuda a explicar
el nombre de la hipótesis.
Prueba para la media (muestra grande).
En las pruebas para la media de población de muestra grande se distingue dos
situaciones:
Conocida la desviación estándar de la población.
Desconocida la desviación estándar de la población.
CONOCIDA LA DESVIACIÓN ESTANDAR POBLACIONAL.
Las pruebas de hipótesis utilizan un procedimiento de cinco pasos, los cuales se
recuerdan a continuación:
a. Plantear las hipótesis nula y alternativa.
b. Determinar el nivel de significancia.
c. Estimar el valor estadístico de prueba.
d. Establecer la regla de decisión.
e. Tomar la decisión.
Dependiendo del planteamiento de la hipótesis alternativa (H1) se distingue dos tipos
de pruebas:
Pruebas bilaterales.
Pruebas unilaterales
PRUEBA BILATERAL
El procedimiento de prueba de hipótesis para pruebas bilaterales a cerca de la
media de una población, cuando se considera el caso de muestra grande ( (n 30) ,
en que el teorema del límite central permite suponer que la media de la
distribución muestral de medias se puede aproximar a una distribución normal de
probabilidad, y la desviación estándar de la población
es conocida, sigue la siguiente forma general:
Muestra grande (n 30)
Planteamiento de hipótesis:
Estadístico de prueba para desviación estándar poblacional conocida:
Regla de rechazo a un nivel de significancia :
Ejemplo
La empresa coca cola ha establecido como política general para su producción en
pequeña escala, un promedio () de llenado para sus envases de 200 centímetros
cúbicos con una desviación estándar () de 16 centímetros cúbicos. Dado que
recientemente se han contratado y diseñado nuevos métodos de producción,
utilizando un nivel de significancia del 0.01, se desea probar la hipótesis, que el
promedio de llenado sigue siendo de 200 centímetros cúbicos.
Para tal efecto se tomó una muestra de 100 envases llenos, los cuales mostraron
una media de llenado de 203.5 centímetros cúbicos.
Solución:
Paso 1
Planteamiento de la hipótesis nula: la media poblacional es 200
Planteamiento de la hipótesis alternativa: La media poblacional es diferente a
200. Estas hipótesis se expresan como sigue:
Esta es una prueba de dos colas, debido a que la hipótesis alternativa ( 0 H ) es
planteada en palabras de diferencia, es decir, la hipótesis no indica si la media es
mayor o menor que 200.
Paso 2
El nivel de significancia es de 0.01 que es el alfa (), la probabilidad de cometer el
error de tipo uno, es decir la probabilidad de rechazar la hipótesis siendo verdadera.
Para éste tipo de problema se utiliza la distribución normal estandarizada en Z.
Paso 3
El valor estadístico de prueba para este tipo de problema es utilizando la
distribución normal estandarizada en Z:
Paso 4
La formulación de la regla de decisión consiste en hallar el valor crítico de Z con
una prueba de dos colas. En el anexo C (tabla de la distribución normal) se identifica
el valor de Z correspondiente a una probabilidad igual a 0.4950 (0.5 . 0.01/2). El valor
más cercano a 0.4950 es 0.4951 que corresponde a una valor de Z igual a 2.58, que es
el valor crítico para la prueba de hipótesis. Dado que es una prueba de dos colas,
se tendrán dos valores críticos, tal como se indica en la siguiente figura:
La regla de decisión es aceptar la hipótesis nula (Ho), puesto que el valor
estadístico de prueba (2.19) ha caído en la zona de aceptación de dicha
hipótesis.
Paso 5
Se concluye que el llenado de los envases cumple con las políticas generales de la
empresa, y la diferencia de promedios se atribuye a variaciones aleatorias.
Prueba para media (pequeña muestra)
Si también es razonable suponer que la población tiene una distribución normal
de probabilidad, con la distribución t se puede hacer inferencia a cerca del valor
de la media de la población.
Ejemplo
Una compañía de seguros revela que en promedio la investigación por
demandas en accidentes y todos los trámites tiene un costo promedio de 60
unidades monetarias. Este costo se considera exagerado comparado con el de otras
compañías del mismo tipo. A fin de evaluar el costo se seleccionó una muestra
aleatoria de 26 demandas recientes y se realizó el estudio de costos. Se concluyó
que el costo promedio es de 57 unidades monetaria con una desviación
estándar de 10 unidades monetarias. Con un nivel de significancia del 0.01 se
puede decir que ¿el estudio reveló un costo menor al establecido por la empresa?
Solución:
Paso 1: La hipótesis nula se plantea en el sentido que el costo promedio es de
60 unidades monetarias.
La hipótesis alternativa que el costo es menor a 60 unidades monetarias. Esto
se expresa en la siguiente forma:
La prueba es de una cola a la izquierda, según el planteamiento de la hipótesis
alternativa.
Paso 2: Se usa un nivel de significancia del 0.01 con una distribución .t., en
consideración a que la muestra en menor a 30, es decir, es una pequeña muestra.
Paso 3: Utilizando los datos de la muestra, se utiliza la siguiente fórmula como
estadístico de prueba:
Paso 4: Los valores críticos para la distribución .t. se encuentran en la tabla
correspondiente (anexo D), con 25 grados de libertad (26 . 1), prueba de una cola a
un nivel de significancia de 0.01, correspondiendo un valor crítico de 2.485. En el
siguiente figura se indica el presente planteamiento:
Paso 5: Puesto que .1.53 se encuentra en la región de aceptación de la hipótesis
nula a un nivel del 1% de significancia, se concluye que los costos para los tramites de
seguros de accidente no se han disminuido y se mantiene a un nivel promedio de costo
de 60 unidades monetarias.