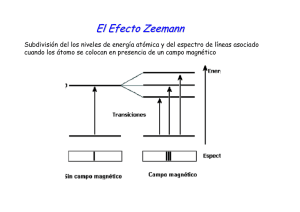
TEMA 4 ESPÍN ELECTRÓNICO 1 El momento angular de espín en átomos monoelectrónicos La ecuación de Schrödinger proporciona un valor excelente para la energía de ionización del átomo de hidrógeno; además, permite explicar muy bien las líneas espectrales de átomos hidrogenoides cuando se utilizan aparatos de baja resolución. En cambio, falla al intentar justificar ciertos detalles que aparecen en estos espectros cuando son realizados con aparatos de alta resolución. En particular, la línea espectral de mayor longitud de onda correspondiente a la serie Lyman1, que parecía simple con aparatos de baja resolución, se separaba en dos líneas (doblete) cuando el espectro del hidrógeno se observaba con aparatos de alta resolución. En 1925 Goudsmit y Uhlenbeck afirmaron que la existencia de dobletes es inconsistente con transiciones entre estados de momento angular 0 y 1. Por otra parte, argumentaron que si al electrón se le asigna un momento angular adicional, de número cuántico s = 1 / 2 , entonces la existencia de ese doblete anómalo puede ser explicada. Goudsmit y Uhlenbeck pensaron que este momento angular adicional debía ser una propiedad intrínseca del electrón y que, desde un punto de vista físico, debería estar relacionado con un movimiento de giro del electrón alrededor de su propio eje (semejante al movimiento de rotación de la tierra). De aquí surgió el nombre de espín2 para denominar esta propiedad del electrón. En 1928 Dirac reformuló el tratamiento de Schrödinger para el átomo monoelectrónico de tal forma que las ecuaciones fueran consistentes con los requerimientos de la teoría de la relatividad. De las soluciones a las ecuaciones de Dirac surgían, de forma natural, los tres números cuánticos ya conocidos (n, l, ml) más un cuarto número cuántico relacionado con esta propiedad intrínseca del electrón que denominamos espín. No obstante lo anterior, en un tratamiento no relativista como el que venimos haciendo, podemos apreciar que la utilización de los operadores escalera (tema 3, apartado 8.5) conduce a la existencia de momentos angulares semienteros (ver ecuaciones (3.165ayb)). Digamos que aunque el espín es un efecto relativista, su inclusión en la mecánica cuántica no relativista no ocasiona ningún desajuste. Puesto que el electrón es una partícula cargada, el espín del electrón debe dar lugar a un momento magnético μ s intrínseco o de espín. Si el electrón pudiera ser descrito como un cuerpo rígido cargado que rota, la relación entre el vector momento magnético de espín, μ s , y el vector momento angular de espín, S , sería la misma que entre μl y L (ver ecuación (3.207)). Sin embargo, al objeto de poder justificar los espectros experimentales observados, Goudsmit y Uhlenbeck propusieron la expresión μs = − g e S 2m (4.1) Donde e es la carga del electrón en valor absoluto y g es un factor denominado factor g de Landé, cuyo valor para el electrón es 2.0024 (aunque para la mayoría de fines 1 Esta línea espectral es la menos energética de la serie Lyman (y por tanto del espectro del hidrógeno). Su origen es una transición entre los orbitales s (l = 0) y p (l = 1). 2 El análisis detallado del espín de una partícula es bastante complejo, y muestra que la propiedad intrínseca asociada no debe considerarse como un giro real de la partícula sobre sí misma; aunque esta imagen física puede resultar útil si se utiliza con cuidado. 1 prácticos podemos tomar g = 2). El signo menos que aparece en la ecuación (4.1) indica que el vector μ s tiene sentido opuesto al vector S . El momento dipolar magnético total de un electrón en su órbita será, por tanto, la suma vectorial ecs. ( 3.207 ) y ( 4.1) e (L + g S ) μ = μl + μ s ⎯⎯ ⎯ ⎯ ⎯ ⎯ ⎯→ μ = − (4.2) 2m que por supuesto depende no sólo de los módulos de L y S, sino también de sus orientaciones relativas. 2 Experimento de Stern y Gerlach La suposición llevada a cabo por Goudsmit y Uhlenbeck sobre la existencia de un momento angular adicional para el electrón, permitió entender el experimento de Stern y Gerlach realizado en 1922. A su vez, dicho experimento puede tomarse como una justificación de la existencia de un momento angular intrínseco (espín) para el electrón. El experimento de Stern y Gerlach se basa en que un campo magnético no homogéneo ejerce fuerzas distintas sobre los polos de un pequeño imán dependiendo de la orientación relativa del imán respecto del campo magnético; y por consiguiente podrá existir una fuerza que provoque el desplazamiento o la desviación de las trayectorias de los pequeños imanes. z fS B x Polos del imán que crea el campo B N y fN N S S Figura 4.1 En la figura 4.1 se ha representado un campo magnético no homogéneo cuya dirección N-S coincide con el eje z. Su intensidad es mayor cuanto más nos acercamos al polo N del imán que lo creó (esto se puede apreciar porque las líneas de campo están más juntas). Si el pequeño imán de la figura cruza el campo magnético según la dirección del eje y, la fuerza magnética sobre el polo S del pequeño imán, fS, es mayor que sobre el polo N, fN. Por lo tanto, existe una fuerza neta sobre el pequeño imán que, en este caso, desvía su trayectoria hacia arriba. Un electrón, debido a su momento angular orbital y a su momento angular de espín, tiene un momento magnético que viene dado por la ecuación (4.2) y, por lo tanto, presenta un comportamiento frente a un campo magnético similar al del pequeño imán de la figura. 2 En el experimento de Stern y Gerlach se hace pasar un haz de átomos hidrogenoides a través de un campo magnético no homogéneo como se muestra en la figura 4.2. El efecto de ese campo sobre un dipolo magnético es ejercer una fuerza cuyo módulo y dirección dependen de la orientación relativa del campo magnético respecto del dipolo. Por ejemplo, si el dipolo magnético es paralelo al campo magnético, tiende a moverse en la dirección en la que el campo magnético aumenta, mientras que si el dipolo magnético es antiparalelo al campo magnético se moverá en la dirección en la que el campo magnético disminuya. Experimento de Stern-Gerlach Figura 4.2 En el experimento de Stern y Gerlach se produce el campo magnético no homogéneo dando a las piezas polares la forma que se muestra en la figura 4.2. En este caso la intensidad del campo magnético aumenta en el sentido S−N. Si los átomos hidrogenoides están es su estado fundamental, el momento angular orbital del electrón es nulo (estado s implica número cuántico l = 0) y todo el momento magnético, de acuerdo con la ecuación (4.2), se deberá al espín. El campo magnético desviará entonces el haz atómico según sea la orientación del momento dipolar magnético μ S o, lo que es lo mismo, la orientación del vector momento angular de espín, S. El resultado del experimento es que el campo magnético no homogeneo desdobla el haz atómico en dos. Esto muestra que el espín del electrón sólo puede tener dos orientaciones respecto al campo magnético: paralelo o antiparalelo. En el apartado 8.6 del tema 3 hemos demostrado que el número de orientaciones posibles para el vector momento angular, respecto de un eje z, es igual a 2l +1 (independientemente de que tomemos l enteros o semienteros). Si, como hemos hecho, llamamos s al número cuántico de espín, puesto que únicamente tenemos dos orientaciones posibles respecto de una dirección z (que hacemos coincidir con el campo magnético), deberá cumplirse 2s +1 = 2 → s = 1 / 2 (como postularon Goudsmit y Uhlenbeck). Denominando ms al número cuántico correspondiente a la componente Sz 3 del vector S, tendremos3 ms = −1/2, +1/2. En la práctica suele denominarse número cuántico de espín a ms (−1/2 y +1/2) y por s se entiende el espín (1/2, sin signo). Las magnitudes del momento angular de espín, S, y su componente z, Sz, vendrán dadas por 3 S = s( s + 1) h = h (puesto que s = 1/2) (4.3) 2 S z = ms h donde ms = ± 1 / 2 (4.4) El caso en el ms = +1 / 2 suele denominarse “spin up” (espín hacia arriba) y cuando ms = −1 / 2 suele denominarse “spin down” (espín hacia abajo). Gráficamente: z 1 Sz = + h 2 θ S= 3 h 2 S= 3 h 2 θ 1 Sz = − h 2 Figura 4.3 De acuerdo con la figura 4.3, la componente S z vendrá dada por S z = S cosθ ; y por tanto, S ± (1 / 2) h ± 1 cosθ = z = = (4.5) S ( 3 / 2) h 3 3 Momento angular de espín y sus operadores Cualquier intento de formular operadores mecanocuánticos para representar el momento angular de espín tropieza con el inconveniente de que no existe el análogo clásico para el espín. Esto no ocurre con el momento angular orbital. De acuerdo con el principio de correspondencia de Bohr, el momento angular orbital mecanocuántico se reduce al momento angular orbital clásico en el caso límite de números cuánticos muy grandes. En cambio, el momento angular de espín simplemente desaparece en el límite clásico (ya que no existe su imagen clásica). Sin embargo, hay buenas razones para pensar que los operadores del momento angular de espín (todavía no definidos) deben presentar ciertas similitudes con los correspondientes operadores del momento angular orbital. Por consiguiente, vamos a dar como postulados la existencia de ciertos operadores que, al aplicar a unas funciones denominadas funciones de espín, conducen a ecuaciones de 3 Recordar que el número cuántico de la componente z del momento angular orbital, ml, va desde –l hasta +l, aumentando de uno en uno. Análogamente, ms debe ir de –s a +s aumentando de uno en uno. Evidentemente, como s = 1/2, sólo tenemos las dos posibilidades indicadas (−1/2 y +1/2). 4 valor propio semejantes a las obtenidas para el momento angular orbital. Así, ) ) definiremos los operadores S 2 y S z de la siguiente forma: ) S 2α = s ( s + 1)h 2α (donde s = 1/2) (4.6a) ) S 2 β = s ( s + 1)h 2 β (s = 1/2) (4.6b) ) 1 S zα = + hα 2 (4.7a) ) 1 S z β = − hβ 2 (4.7b) Puesto que las funciones propias de espín no incluyen coordenadas espaciales, únicamente existen dos funciones de este tipo, que representaremos por α y β. Obviamente desconocemos la forma analítica de dichas funciones, pero nos es ) suficiente con saber que una es la función propia del operador S z con valor propio ) +1/2 h (la función α), y la otra (la función β) es la función propia de S z con valor propio -1/2 h . Admitiremos que las funciones propias α y β son ortonormales; es decir, α | α = ∫ α *α dσ = β | β = ∫ β * β dσ = 1 (4.8a) α | β = ∫ α * β dσ = β | α = ∫ β *α dσ = 0 (4.8b) donde σ es lo que llamamos variable de espín, que no tiene el análogo clásico. Puesto que el operador hamiltoniano que hemos considerado (operador hamiltoniano no relativista) no contiene coordenadas de espín (operador hamiltoniano libre de espín), se cumplirán las siguientes relaciones de conmutación: ) ) ) ) Sz , H = 0 y S 2,H = 0 (4.9) [ [ ] ] Por la misma razón, tendremos idénticas relaciones de conmutación con los operadores ) ) L2 y L z ; es decir, [S) , L) ] = [S) , L) ] = [S) 2 z z z 2 ] [ ] ) ) ) , L2 = S 2 , L z = 0 (4.10) Por consiguiente, la magnitud del momento angular de espín, su componente z, la energía, la magnitud del momento angular orbital y su componente z podrán ser determinadas simultáneamente. 4 Acoplamiento espín-órbita en átomos hidrogenoides En general un electrón de un átomo posee un momento angular orbital, caracterizado por el número cuántico l, y un momento angular de espín, caracterizado por el número cuántico s. Sistemas clásicos análogos que poseen dos tipos de momento angular son la tierra (que está girando alrededor de su eje de rotación además de trasladarse alrededor del sol) y un giroscopio con precesión (que tiene momento angular de precesión además 5 del movimiento de rotación alrededor de su eje). El momento angular total de estos cuerpos será la suma vectorial de ambos momentos angulares, J = L + S . Desde un punto de vista clásico, el momento angular total J es una magnitud importante debido a que su variación con el tiempo coincide con el momento resultante de las fuerzas que actúan sobre el sistema. Obviamente, en el caso de fuerzas centrales el momento de las mismas es nulo y, por tanto, el momento angular total se conserva. En el caso de un sistema clásico, el módulo del momento angular total puede tener cualquier valor comprendido entre | L − S | y | L + S | . En cambio, como ya hemos visto, en mecánica cuántica tanto el vector L como el vector S están cuantizados y sus direcciones están restringidas. Las reglas mecano-cuánticas para combinar momentos angulares orbitales y de espín (o dos momentos angulares cualesquiera pertenecientes a dos partículas) no son sencillas de deducir pero sí de aplicar. Para el caso que nos ocupa (interacción de los momentos angulares de órbita y de espín de una misma partícula) el momento angular total J tendrá un módulo dado por J= j ( j + 1) h (4.11) donde el número cuántico j podrá tener alguno de los valores j =| l + s | ⎫ ⎪ o ⎬ j = | l − s | ⎪⎭ (4.12) Nótese que si l = 0 (orbital tipo s), únicamente tenemos un valor para el momento angular total j; es decir j = s =1/2. Para un valor de l ≠ 0 , por ejemplo l = 1 , tendremos j = 3 / 2 y j = 1 / 2 . Utilizando la notación espectroscópica los estados cuánticos del átomo de hidrógeno se representan mediante un símbolo del tipo n 2 s +1l j . Puesto que s = 1/2 el término queda n 2 l j ; donde n es el número cuántico principal, l es el número cuántico orbital y j es el número cuántico asociado al momento angular total (que viene dado por (4.12)). Es costumbre remplazar el valor numérico de l por una letra mayúscula de acuerdo con las siguientes equivalencias: ⎧ 0 1 2 3 4 ... l=⎨ ⎩ S P D F G ... Para el caso de átomos hidrogenoides (que es el caso que nos ocupa) pueden utilizarse letras minúsculas en lugar de utilizar, como hemos hecho, letras mayúsculas; pero en el caso de átomos en general (que se verá más adelante) es obligatorio el uso de las letras mayúsculas. Utilizando la terminología anterior, el estado fundamental del hidrógeno será 1 2 S1 / 2 (puesto que l = 0, j sólo tiene el valor 1/2). Para el número cuántico principal n = 2, tenemos los valores l = 0 y l = 1 . Si l = 0 necesariamente j = 1 / 2 , pero si l = 1 6 tendremos j = 1 / 2 y j = 3 / 2 . Por tanto, para n = 2 tendremos los estados 2 2 S1 / 2 , 2 2 P1 / 2 y 2 2 P3 / 2 . En átomos hidrogenoides se asume que los estados con un mismo valor de n y j, pero con distinta l, tienen igual energía (energía de 2 2 P1 / 2 = energía de 2 2 S1 / 2 ). En cambio, dos estados con idénticos valores de n y l, pero con valores distintos de j, tienen energías ligeramente diferentes debido a la interacción del espín del electrón con su movimiento orbital. Este efecto es lo que denominamos interacción o acoplamiento espín-órbita. Así, energía 2 2 P3 / 2 > energía 2 2 P1 / 2 (sólo ligeramente mayor). La interacción espín-órbita permite justificar, por ejemplo, la existencia de un doblete para la línea de mayor longitud de onda (y por tanto, de menor energía) de la serie Lyman. En efecto, 2 2P3 / 2 2p 2 2P1 / 2 1ª línea serie Lyman 1 2 S1 / 2 1s Con interacción espín-órbita Sin interacción espín-órbita Figura 4.4 5 Efecto Zeeman anómalo Si tenemos en cuenta el momento angular de espín como una parte del momento angular total del electrón, debemos reformular el efecto Zeeman visto en el tema 3 al objeto de contemplar la interacción del campo magnético con el momento angular total (y no únicamente con el momento angular orbital, que es lo que vimos en el tema 3). Sin entrar en justificaciones teóricas, diremos que cuando se contempla la interacción espín-orbital, el efecto de un campo magnético es eliminar las (2 j + 1) degeneraciones de un estado n 2 l j . Por tanto, un estado n 2 S1 / 2 se transforma, en presencia de un campo magnético, en dos estados energéticos diferentes, uno con m j = 1 / 2 y otro con m j = −1 / 2 (con energías por encima y por debajo, respectivamente, a la energía del estado n 2 S1 / 2 en ausencia de campo magnético). Análogamente, los estados n 2 P1 / 2 y n 2 P3 / 2 se desdoblarán, respectivamente, en 2 y 4 estados (de acuerdo con el valor de (2 j + 1) para cada caso). 7 Las transiciones entre los estados originados deben cumplir unas reglas llamadas reglas de selección (esto se verá con profundidad en la asignatura de cuarto, Química Física II). De momento nos limitaremos a enunciar dichas reglas: Para que una transición entre dos estados energéticos esté permitida, deben cumplirse los siguientes requisitos para los números cuánticos: Δn = cualquiera Δl = ±1 Δj = 0, ± 1 Δm j = 0, ± 1 (4.13) En la figura siguiente se ha dibujado el desdoblamiento de los niveles energéticos de la figura 4.4 cuando consideramos la presencia de un campo magnético: mj = 3/2 2 2 P3 / 2 mj = 1/2 mj = −1/2 mj = −3/2 2p mj = 1/2 2 1s 2 P1 / 2 mj = −1/2 12 S1 / 2 mj = 1/2 mj = −1/2 B=0y sin interacción espín-orbital B ≠ 0y con interacción espín-orbital B=0y con interacción espín-orbital Las transiciones dibujadas obedecen las reglas de selección. Nótese cómo al considerar un campo magnético pasamos de 2 transiciones (B = 0 con interacción espín-orbital) a 10 (B ≠ 0 con interacción espín-orbital). Las lineas dibujadas corresponderían a un espectro de emisión (cambiándoles el sentido a las flechas tendríamos las líneas correspondientes a un espectro de absorción). 6 Espinorbitales Hemos denominado orbitales a las funciones propias del operador hamiltoniano (no ) h2 2 relativista) del átomo de hidrógeno, H = − ∇ + V , donde V es la energía potencial 2m del electrón en el campo eléctrico del núcleo ( Ke 2 / r ). Estos orbitales son funciones de las coordenadas espaciales ( r ,θ ,φ ). La función de onda del átomo de hidrógeno, además de las coordenadas espaciales, debe tener la variable de espín σ . Esta variable no tiene correspondencia clásica, por lo que no podemos hacernos una imagen sencilla de ella. De acuerdo con lo anterior, la función de onda del átomo de hidrógeno no será un orbital, sino que será una función que dependerá de las coordenadas espaciales y de 8 la coordenada de espín del electrón: Ψ (r ,θ ,φ ;σ ) 4 . Puesto que el hamiltoniano no relativista (que es el que hemos venido considerando) depende únicamente de las coordenadas espaciales, Ψ (r ,σ ) será función propia de dicho hamiltoniano, ) HΨ (r , σ ) = EΨ (r , σ ) , y podemos factorizar la función de onda como el producto del orbital ψ (r ) y de una función de espín η (σ ) Ψ (r ,σ ) = ψ (r )η (σ ) (4.14) siendo η (σ ) una de las funciones propias de espín α (σ ) o β (σ ) (que abreviadamente escribimos como α o β). Ψ (r ,σ ) , o equivalentemente ψ (r )η (σ ) , es lo que llamamos un espinorbital. Obsérvese que para un determinado orbital ψ (r ) tendremos dos posibles espinorbitales: ψ (r )α y ψ (r ) β . También debemos tener en cuenta que dos espinorbitales serán ortogonales bien porque lo sean los orbitales, o porque lo sean las funciones de espín (o evidentemente porque lo sean ambos). Así, por ejemplo, ψ (r )α | ψ (r ) β = ψ (r ) | ψ (r ) α | β = 0 , a pesar de que ψ (r ) | ψ (r ) =1 (si el orbital ψ (r ) está normalizado). Al objeto de abreviar la escritura, las coordenadas de la posición (r,θ,φ) las representaremos simplemente por r. De esta forma, podemos expresar un orbital como ψ(r) en lugar de ψ(r,θ,φ). 4 9 10 EJERCICIOS TEMA 4 *4.1 Un átomo de hidrógeno está en el estado 3D. a) ¿Cuáles son los valores posibles j? b) ¿Cuáles son los valores del módulo del momento angular total? c) ¿Cuáles son las posibles componentes z del momento angular total? Solución.- a) 3/2, 5/2. b) 1.936 h , 2.958 h . c) -3/3 h , -1/2 h , 1/2 h , 3/2 h ; -5/2 h , 3/3 h , -1/2 h , 1/2 h , 3/2 h , 5/2 h . 4.2 Las líneas dobletes amarillas características del espectro del sodio son el resultado de transiciones de los estados 3P3 / 2 y 3P1 / 2 al estado fundamental 3S1 / 2 . Las longitudes de onda de estas dos líneas son 589.6 nm y 589.0 nm. a) Calcular las energías en eV de los fotones correspondientes a estas longitudes de onda. b) La diferencia de energía de estos fotones es igual a ΔE de los estados 3P3 / 2 y 3P1 / 2 . Esta diferencia de energía se debe al efecto espín-órbita. Calcular ΔE . Solución.- b) ΔE = 0.0022 eV. 4.3 Para el multiplete 2 P se pide: a) ¿Cuáles son los términos espectroscópicos completos asociados? b) En ausencia de campo magnético, ¿cuántos niveles de energía existen? c) En presencia de un campo magnético, ¿en cuántos niveles de energía se desdobla cada uno de los niveles energéticos del apartado anterior? Solución.- a) 2 P3 / 2 , 2 P1 / 2 ; b) 2; c) 4 y 2, respectivamente. 4.4 Dibuja el diagrama de niveles de energía para las transiciones entre los estados 2 P3 / 2 y 2 D3 / 2 en el átomo de hidrógeno. Suponer presencia de campo magnético. Nota.- El estado 2 P3 / 2 procede del nivel n = 2 y 2 D3 / 2 del n = 3. *4.5 En el formalismo de Pauli para la representación matricial de las funciones de ) ) espín α y β, y los operadores S z y S 2 , las funciones vienen dadas por vectores columna y los operadores por matrices 2 × 2. Así, se tiene: ⎛1⎞ ⎛ 0⎞ ) h ⎛1 0⎞ ) h 2 ⎛ 3 0⎞ ⎜ ⎟ ⎟⎟ y S 2 = α = ⎜⎜ ⎟⎟ , β = ⎜⎜ ⎟⎟ , S z = ⎜⎜ 2 ⎝ 0 − 1⎠ 4 ⎜⎝ 0 3 ⎟⎠ ⎝ 0⎠ ⎝1⎠ Se pide: ) ) ) ) h h a) S zα = α , S z β = − β , S 2α = s ( s + 1)h 2α y S 2 β = s ( s + 1)h 2 β 2 2 b) Puesto que el conjunto (α, β) constituye un conjunto ortonormal completo de funciones de espín, cualquier función de espín monoelectrónica puede escribirse como c1 α + c2 β (donde c1 y c2 son constantes). Demuestra, utilizando la notación matricial ) de Pauli, que c1 α + c2 β no es función propia del operador S z pero sí lo es del operador ) S2 . 11 4.6 Los operadores de espín de Pauli para matricialmente por ) ) h ⎛0 1⎞ ) h ⎛0 − i⎞ ⎟⎟ , S y = ⎜⎜ ⎟⎟ y S z = S x = ⎜⎜ 2 ⎝1 0⎠ 2⎝i 0 ⎠ Se pide: a) Calcular el conmutador [ Sˆ x , Sˆ y ] . las tres direcciones se representan h ⎛1 0 ⎞ ⎜ ⎟ 2 ⎜⎝ 0 − 1⎟⎠ b) Calcular Ŝ 2 como suma de los cuadrados de Ŝ x , Ŝ y y Ŝ z . c) Comprobar que Ŝ 2 conmuta con Ŝ x . 3 ⎛1 0⎞ ⎟. Solución.- a) ih Sˆ z ; b) h 2 ⎜⎜ 4 ⎝ 0 1 ⎟⎠ 4.7 Completa la siguiente tabla para un átomo de hidrógeno: Configuración electrónica Símbolos espectroscópicos 2 S +1 Xj Degeneración con B ≠ 0 1s1 2s1 2p1 3s1 3p1 3d1 b) Dibuja un diagrama de niveles energéticos (en ausencia de campo magnético externo) para los posibles estados n =2 y n =3 y especifica las transiciones posibles entre estos dos subniveles (en el caso de un espectro de emisión). 1 1 . Un 2 n2 átomo de hidrógeno se encuentra en un estado dado por la función normalizada 1 1 ψ = 3d z 2 + i (2 p0 − 2 p −1 ) Σ , siendo Σ = (α − β ) . 3 2 *4.8 La energía de un átomo de hidrógeno en unidades atómicas es E n = − ( ) Calcular Ĥ , L̂2 , L̂ z , Ŝ 2 y Ŝ z . Solución.- -0.102 u.a., 10/3 u.a., -1/3 u.a., 3/2 u.a. y 0 u.a. (respectivamente). 12