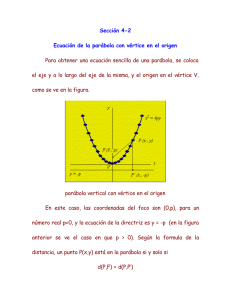
El cable de suspensión de un puente colgante adquiere la forma de un arco de parábola. Los pilares que lo soportan tienen una altura de 60 m y están separados a una distancia de 500 m. Quedando el punto más bajo del cable a una altura de 10 m sobre la calzada del puente. Tomando como eje x la horizontal que define el puente y como eje Y el de simetría de la parábola, halle la ecuación de tal parábola. Calcule la altura de un punto situado a 80 m del centro del puente 60m Vértice: (h,k) 10m (0,0) 250m 250m Utilizaremos la ecuación de la parábola en función de su vértice (h,k), En este caso, si ubicamos nuestro eje de referencia en la base del pilar de la izquierda (ese será el punto (0,0) señalado en la figura), el vértice es (0, 10), con lo que tenemos los valores de h y k de nuestra ecuación, la cual quedará como Para determinar , utilizamos un punto cualquiera de la parábola y sustituimos sus coordenadas en la ecuación. Usemos el punto donde el cable se apoya del pilar de la derecha. Ese punto es (250,60). Por tanto, podemos escribir: De donde podemos despejar , Ya tenemos la ecuación de la parábola: La altura de un punto situado a 80 m del centro del puente será: