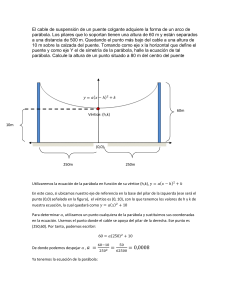
UNIDAD EDUCATIVA FISCAL “JOSÉ JOAQUÍN PINO YCAZA” AMIE: 09H01742 PROYECTO CIENTÍFICO 06 DÉCIMO BÁSICA SUPERIOR CICLO COSTA AÑO LECTIVO 2021-2022 Objetivo de aprendizaje: Objetivos específicos: Indicadores de evaluación: Proyecto: Los estudiantes comprenderán la complejidad de los seres vivos para inferir las repercusiones de la acción humana en el medio ambiente, desde lo local hasta lo global, por medio de una comunicación empática en la que se incentive la toma de decisiones acertadas en el mantenimiento de la dinámica de los ecosistemas. Aplicar métodos, técnicas matemáticas y estadísticas de manera apropiadas en situaciones de la vida cotidiana relacionadas al estudio de la Biodiversidad, Medioambiente y Ecosistemas. I.M.4.3.4. Utiliza las TIC para graficar funciones lineales, cuadráticas y potencia (n=1, 2, 3), y para analizar las características geométricas de la función lineal (pendiente e intersecciones), la función potencia (monotonía) y la función cuadrática (dominio, recorrido, monotonía, máximos, mínimo, paridad); reconoce cuándo un problema puede ser modelado utilizando una función lineal o cuadrática, lo resuelve y plantea otros similares. (J.1., I.4.) DERECHOS CIUDADANOS Y AMBIENTALES En este proyecto vamos a elaborar un Materiales: Para esta actividad puedes utilizar los siguientes materiales: Ficha guía del estudiante. Hojas en blanco, hojas de cuadro, papel ministro o cualquier papel reciclable que tengas disponible. Revistas, periódicos, recortes de imágenes. Internet, celular, laptops. Lápices de cualquier color (pinturas), marcadores u otros materiales para escribir. Calculadora científica. Juego Geométrico. Plataformas y herramientas digitales. Indicaciones: Recuerda que puedes utilizar cualquier otro material que esté a tu alcance en el hogar o materiales reutilizados Actividades para la semana 1 Tema: FUNCIONES PARÁBOLAS CUADRÁTICAS ¿Sabías qué…? Cuando tus lanzas una moneda al aire, la trayectoria de la moneda se denomina PARÁBOLA, la misma que se puede describir mediante una función matemática denominada CUADRÁTICA. FUNCIÓN y = x2 La curva que describe un balón cuando se lanza a canasta es una parábola. También describen parábolas las bolas de golf o los chorros de agua. Parabólicas son las secciones de las antenas que captan las emisiones de televisión procedentes de los satélites artificiales y las secciones de los faros de los coches. También hay muchas funciones que se representan mediante parábolas: — El área de un cuadrado en función de su lado (A = l2) o la de un círculo en función de su radio (A = πr2). — La altura a la que se encuentra una piedra que lanzamos hacia arriba en función del tiempo transcurrido desde que se lanzó (a = v0t – 4,9t2). — El espacio que recorre un coche desde que decidimos frenar hasta que realmente se para, en función de la velocidad que llevaba (e = 0,0074v2 + 0,21v). Actividades: 1. Leer la siguiente introducción sobre FUNCIONES CUADRÁTICAS. 2. Realizar las actividades propuestas por el docente. FUNCIÓN CUADRÁTICA y = ax 2 • Cuando a > 0, la gráfica de la función y = ax 2 es una parábola abierta hacia arriba (en forma de vaso). Cuando a < 0, es una parábola abierta hacia abajo (en forma de campana). • En las parábolas de ecuación y = ax 2, el eje Y es su eje de simetría. EJEMPLO a) 𝒚 = 𝒙𝟐 b) 𝒚 = 𝟐𝒙𝟐 𝟏 𝟐 𝒚 = 𝒙𝟐 c) Las tres parábolas tienen forma de vaso. Vemos que la parábola 𝑦 = 2𝑥 2 es más estrecha que la parábola 1 𝑦 = 𝑥 2 En cambio, la parábola 𝑦 = 2 𝑥 2 es más ancha que la parábola 𝑦 = 𝑥 2 . a) 𝒚 = −𝒙𝟐 b) 𝒚 = −𝟐𝒙𝟐 c) 𝟏 𝒚 = − 𝟐 𝒙𝟐 Estás tres parábolas son iguales que las anteriores, pero están abiertas hacía abajo, y tienen forma de campana. Actividad propuesta. Sin representarlas, di cuáles de las siguientes parábolas tienen forma de vaso o de campana y cuáles son más anchas o estrechas que y = x 2. 𝟏 𝟏 a) 𝒚 = 𝟒 𝒙𝟐 b) 𝒚 = − 𝟑 𝒙𝟐 c) 𝒚 = −𝟕𝒙𝟐 d) 𝒚 = 𝟓𝒙𝟐 𝟓 e) 𝒚 = 𝟑 𝒙𝟐 f) 𝒚 = −𝟗𝒙𝟐 Los puentes colgantes, la función cuadrática y el medio ambiente. Al construir un puente se logra ayudar al medioambiente ya que se reducen las distancias y por lo tanto se consume menos gasolina, dando como resultado la reducción de la emisión de CO2. La matemática es muy útil al momento de diseñar un puente colgante ya que utilizando las funciones cuadráticas podemos calcular de una manera muy precisa las diferentes dimensiones del mismo, permitiéndonos ahorrar en material y tiempo, contribuyendo al medio ambiente al evitar desperdiciar los diferentes componentes que se utilizan en su construcción. Golden Gate Es un ejemplo de puente colgante. Une la ciudad de San Francisco con los suburbios del norte. Fue el puente más largo del mundo hasta 1964, cuando fue superado por el puente de Verrazano, Nueva York. Su construcción ha planteado complejos problemas técnicos a lo largo de la historia. Alcanza su máxima expresión en los puentes colgantes, los más largos del mundo. Actividades para la semana 2 Tema: FUNCIONES CUADRÁTICAS TRASLACIONES DE LA FUNCIÓN 𝒚 = 𝒙𝟐 . TRASLACIONES VERTICALES. ¿Sabías qué…? Se puede utilizar la factorización para analizar las funciones cuadráticas. TRASLACIONES VERTICALES La gráfica de y = x 2 + k se obtiene trasladando verticalmente k unidades la gráfica de y = x 2. • Si k > 0, la traslación vertical es hacia arriba. • Si k < 0, la traslación vertical es hacia abajo. EJEMPLO Representa las siguientes funciones. a) y = x 2 + 5 b) y = x 2 – 5 x −2 −1 0 1 2 x −2 −1 0 1 2 y 9 6 5 6 9 y −1 −4 −5 −4 −1 La parábola y = x 2 + 5 es igual que y = x 2, pero trasladada 5 unidades hacia arriba, mientras que la parábola y = x2 − 5 es igual que y = x 2, pero trasladada 5 unidades hacia abajo. El vértice de y = x 2 + 5 está en V (0, 5), mientras que el vértice de y = x 2 − 5 está en V' (0, −5). Así, el eje de simetría es igual en ambas gráficas: el eje Y, y pasa por el vértice de cada una de ellas. TAREA. Representa sobre el mismo plano cartesiano, con colores diferentes, las siguientes parábolas. a) 𝒚 = 𝒙𝟐 − 𝟏 b) 𝒚 = 𝒙𝟐 + 𝟏 c) 𝒚 = 𝒙𝟐 + 𝟑 Actividades para la semana 3 Tema: FUNCIONES CUADRÁTICAS TRASLACIONES DE LA FUNCIÓN 𝒚 = 𝒙𝟐 . TRASLACIONES HORIZONTALES. TRASLACIONES HORIZONTALES La gráfica de y = (x + h)2 se obtiene trasladando horizontalmente h unidades la gráfica de y = x 2. • Si h > 0, la traslación horizontal es hacia la izquierda. • Si h < 0, la traslación horizontal es hacia la derecha. EJEMPLO Representa las siguientes funciones. a) 𝒚 = (𝒙 + 𝟐)𝟐 x −2 −1 0 1 2 y 0 1 4 9 16 b) 𝒚 = (𝒙 − 𝟐)𝟐 x −2 −1 0 1 2 y 16 9 4 1 0 La parábola y = (x + 2)2 es igual que y = x 2, pero trasladada 2 unidades hacia la izquierda, mientras que la parábola y = (x − 2)2 es igual que y = x 2, pero trasladada 2 unidades hacia la derecha. El vértice de y = (x + 2)2 está en V (−2, 0), mientras que el vértice de y = (x − 2)2 está en V'(2, 0). Así, el eje de simetría de la parábola y = (x + 2)2 es la recta x = −2, mientras que el eje de y = (x − 2)2 es la recta x = 2, que es paralela al eje Y. TAREA. Representa sobre el mismo plano cartesiano, con colores diferentes, las siguientes parábolas. 𝟐 a) 𝒚 = (𝒙 − 𝟏) 𝟐 b) 𝒚 = (𝒙 + 𝟏) 𝟐 c) 𝒚 = 𝒙 + 𝟑 Actividades para la semana 4 Tema: FUNCIONES CUADRÁTICAS TRASLACIONES DE LA FUNCIÓN 𝒚 = 𝒙𝟐 . TRASLACIONES HORIZONTALES Y VERTICALES. TRASLACIONES VERTICALES Y HORIZONTALES La gráfica de y = (x − h)2 + k es una parábola como la gráfica de y = x2, pero con el vértice en el punto (h, k). EJEMPLO Representa las siguientes funciones. a) 𝒚 = (𝒙 − 𝟐)𝟐 + 𝟑 x 0 1 2 3 4 y 0 1 4 9 16 Si trasladamos la parábola y = x 2 en 2 unidades a la derecha se obtiene la parábola y = (x − 2)2. Si a continuación trasladamos esta parábola en 3 unidades hacia arriba, obtenemos la parábola de ecuación y = (x − 2)2 + 3. El vértice de y = (x − 2)2 + 3 está en el punto (h, k) = (2, 3).Su eje de simetría es la recta x = 2, que es paralela al eje Y. TAREA. A partir de la parábola 𝒚 = 𝒙𝟐 representa las siguientes parábolas sobre el mismo plano cartesiano, con colores diferentes, explicando como lo haces. 𝟐 a) 𝒚 = (𝒙 + 𝟐) − 𝟑 𝟐 b) 𝒚 = (𝒙 + 𝟏) + 𝟑 𝟐 c) 𝒚 = (𝒙 − 𝟑) − 𝟏 Actividades para la semana 5 Tema: FUNCIONES CUADRÁTICAS APLICACIONES DE LA FUNCIÓN CUADRÁTICA 𝒚 = 𝒙𝟐 EN LA VIDA COTIDIANA. ¿Sabías qué…? Gracias al conocimiento sobre la ecuación cuadrática se han podido construir verdaderas obras maestras de ingeniería como el famoso puente GOLDEN GATE situado a la entrada de San Francisco, el mismo que tiene una forma de parábola. El puente Golden Gate enmarca la entrada a la bahía de San Francisco. Sus torres de 746 pies de altura están separadas por una distancia de 4200 pies. El puente está suspendido de dos enormes cables que miden 3 pies de diámetro: el ancho de la calzada es de 90 pies y ésta se encuentra aproximadamente a 220 pies del nivel del agua. Los cables forman una parábola y tocan la calzada en el centro del puente. Determinar la altura de los cables a una distancia de 1000 pies del centro del puente. (Ubicar este problema en su octaedro ecológico). Solución. Empezamos seleccionando la ubicación de los ejes de coordenadas de modo que el eje x coincida en la calzada y el origen coincida en el centro del puente. Como resultado de esto, las torres gemelas quedarán a 746-220=526 pies arriba de la calzada y ubicadas a 42002=2100 pies del centro. Los cables de forma parabólica se extenderán desde las torres, abriendo hacia arriba, y tendrán su vértice en (0,0) como se ilustra en la figura de abajo. Nota: Observar que 2100′ = 2100𝑝ⅈⅇ𝑠 La manera en que seleccionamos la colocación de los ejes nos permite identificar la ecuación de una parábola como 𝒚 = 𝒂𝒙𝟐 , 𝒂 > 𝟎. Obsérvese que los puntos (−2100,526) y (2100,526) están en la gráfica parabólica. Con base en estos datos podemos encontrar el valor de a en 𝒚 = 𝒂𝒙𝟐: 𝒚 = 𝒂𝒙𝟐 𝟓𝟐𝟔 = 𝒂(𝟐𝟏𝟎𝟎)𝟐 𝟓𝟐𝟔 𝒂 = (𝟐𝟏𝟎𝟎)𝟐 Así la ecuación de la parábola es 𝟓𝟐𝟔 𝒚 = ((𝟐𝟏𝟎𝟎)𝟐 ) 𝒙𝟐 La altura del cable cuando 𝒙 = 𝟏𝟎𝟎𝟎 es 𝟓𝟐𝟔 𝒚 = ((𝟐𝟏𝟎𝟎)𝟐 ) (𝟏𝟎𝟎𝟎)𝟐 𝟓𝟐𝟔 𝒚 = (𝟐𝟏𝟎𝟎∗𝟐𝟏𝟎𝟎) (𝟏𝟎𝟎𝟎)𝟐 𝒚=( 𝟓𝟐𝟔 𝟒𝟒𝟏𝟎𝟎𝟎𝟎 ) (𝟏𝟎𝟎𝟎 ∗ 𝟏𝟎𝟎𝟎) 𝟓𝟐𝟔 𝒚 = (𝟒𝟒𝟏𝟎𝟎𝟎𝟎) (𝟏𝟎𝟎𝟎 ∗ 𝟏𝟎𝟎𝟎) 𝒚 = (𝟎. 𝟎𝟎𝟎𝟏𝟏𝟗𝟐𝟕)(𝟏𝟎𝟎𝟎𝟎𝟎𝟎) 𝒚 = 𝟏𝟏𝟗, 𝟐𝟕 𝒚 ≈ 𝟏𝟏𝟑𝒑ⅈⅇ𝒔 “Una maravilla moderna” Su construcción a planteado complejos problemas técnicos a lo largo de la historia. Alcanza su máxima expresión en los puentes colgantes, los más grandes del mundo. Golden Gate Es un ejemplo de puente colgante. Une la ciudad de San Francisco con los suburbios del norte. Fue el puente más largo del mundo hasta 1964, cuando fue superado por el puente de Verrazano, en NEW YORK. Joseph Baermann Strauss Charles Alton Ellis Charles Alton Ellis fue un profesor, ingeniero estructural y matemático que fue el principal responsable del diseño estructural del puente Golden Gate. Debido a una disputa con Joseph Strauss, no fue reconocido por su trabajo cuando se inauguró el puente en 1937. Joseph Baermann Strauss fue un ingeniero estructural estadounidense que revolucionó el diseño de puentes basculantes. Fue el ingeniero jefe del puente Golden Gate, un puente colgante a la entrada de San Francisco. Tarea: En base al ejercicio sobre el puente GOLDEN GATE determinar la altura de los cables a una distancia de 50 pies del centro del puente. Observar que 50′ = 50𝑝ⅈⅇ𝑠 Compromisos Me comprometo a: Trabajar mis tareas con puntualidad y responsabilidad. Educarme en sexualidad como parte del desarrollo humano integral con responsabilidad en principios y valores. Desarrollar el hábito de investigar en beneficio personal. Cuidarme y proteger mi cuerpo para desarrollar una sexualidad responsable, de abusos y violencia ante posibles situaciones de riesgo y vulnerabilidad. Impulsar los valores impartidos, para ser proactivo y dinámico. Autoevaluación Autoevaluación: ¿Qué aprendí sobre los temas estudiados? ¿Qué conozco sobre Educación sexual? ¿Para qué me sirven tener una buena educación sexual? ¿La convivencia familiar armónica nos permite ser mejores personas? ¿Por qué? ¿Tener una comunicación asertiva nos ayuda a tener relaciones interpersonales fortalecidas? ¿Qué haces por vivir en una sana convivencia familiar?