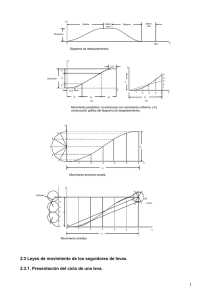
LEVAS La leva es un elemento mecánico de una maquinaria que se utiliza para conducir mediante contacto directo otro elemento, llamado seguidor o vástago, según un movimiento especificado. Las levas ofrecen un medio excelente de transformar un movimiento giratorio en alternativo. Como pueden darse muchas formas diferentes al contorno de la leva, existen muchos tipos de movimiento para el seguidor. CLASIFICACIÓN DE LAS LEVAS Y SEGUIDORES a) Los seguidores se clasifican: Traslación De acuerdo a su movimiento en: oscilación Radial Por la trayectoria que siguen respecto del centro de la leva Transversal De acuerdo con el tipo de contacto _ de filo de cuchillo _ de pie plano o cara plana _ de contacto esférico o puntual _ de Rodillo. b) Las levas se clasifican de acuerdo a su forma: _ Levas de plato o de placa, o plana, de disco o radiales _ Levas de cuña. _ Levas cilíndrica. _ Leva transversal. _ Leva de yugo. Leva de cuña con seguidor de rodillo y con movimiento de traslación Leva cilindrica Leva de disco Leva plana con seguidor radial Leva plana con seguidor de contacto esférico Leva cónica Leva de plato con seguidor de rodillo Leva plana con seguidor de filo de cuchillo Leva de disco con seguidor de cara plana La leva gira a velocidad angular constante y hace que el seguidor se traslade a lo largo de una línea radial que pase el centro de la leva. Para cada posición de la leva hay una posición correspondiente del seguidor. Para definir la superficie de la leva por medios gráficos es importante, recordar que hay que mantener la leva estacionaria y girar el seguidor en sentido opuesto al de la leva. 1- Circunferencia base, es la más pequeña tangente al contorno de la leva y su tamaño determina el tamaño de la leva. 2- Punto de trazo, es un punto teórico sobre el seguidor de la leva, corresponde al punto de un seguidor de filo de cuchillo y se utiliza para generar la curva primitiva. 3- Ángulo de presión, formado por la dirección del movimiento del seguidor y una normal a la curva primitiva. Si el ángulo es grande se apoyará fuertemente en sus cojinetes o guías. La existencia del ángulo de presión implica que las fuerzas existentes entre la leva y el seguidor no están en la misma dirección que el movimiento del seguidor 4- Punto primitivo, indica la situación del ángulo máximo de presión. 5- Circunferencia primitiva, es una circunferencia concéntrica en la leva y que pasa por los puntos primitivos. 6- Circunferencia principal, es la menor circunferencia concéntrica con la leva y tangente a la curva primitiva. Los puntos de inflexión o de transición del diagrama se corresponden con los puntos primitivos. Estos puntos, coinciden con la máxima pendiente de la curva primitiva. Geometría de una leva DIAGRAMAS DE DESPLAZAMIENTOS Los movimientos más utilizados para la construcción del perfil de las levas son los movimientos: Uniforme modificado, armónico, parabólico y cicloidal A) MOVIMIENTO UNIFORME El diagrama de desplazamiento para movimiento uniforme es una recta de pendiente constante. Los desplazamientos del seguidor son iguales para intervalos de tiempos iguales. Es un movimiento que no se utiliza en la práctica debido a los cambios bruscos que se origina el comienzo y final de la carrera, lo que se traduce en grandes esfuerzos, inconveniente sobre todo cuando la leva gira a elevadas velocidades. V= Cte. a=O Elevación (ángulo de la leva) B) MOVIMIENTO UNIFORME MODIFICADO Para evitar el inconveniente que tiene el movimiento uniforme se hace una modificación, de tal forma que el seguidor aumente gradualmente su velocidad al inicio de la carrera y disminuya gradualmente al final. Se trazan arcos de circunferencia en los extremos de diagrama uniforme. Generalmente se toma un radio igual al desplazamiento. MOVIMIENTO ARMÓNICO La aceleración es variable. - Una semi circunferencia con diámetro = elevación del seguidor. Se divide en el mismo número de partes que se ha dividido el eje de las abscisas. El movimiento armónico simple, tiene la ventaja que con un seguidor radial de rodillo el ángulo máximo de presión es menor que con el movimiento parabólico con intervalos iguales o con movimiento cicloide; permitiendo que se apoye rígidamente menos y sobre salga más en su construcción (por estas razones se prefiere el movimiento armónico simple a los otros tipos). Durante años, el diseño de levas se concretó a mover un seguidor a lo largo de una distancia determinada durante un determinado tiempo. Las velocidades eran bajas, de manera que las fuerzas de aceleración no eran importantes. Sin embargo con la tendencia a mayores velocidades de máquinas, ha sido necesario tener en cuenta las características dinámicas del sistema y seleccionar un contorno de leva que minimice la carga dinámica. A manera de ejemplo de la importancia de la carga dinámica, consideramos el movimiento parabólico. Este movimiento parecería ser muy deseable en base a las fuerzas de inercia debido a su baja aceleración. Sin embargo, no se puede ignorar el hecho de que la aceleración aumenta desde cero a su valor constante casi instantáneamente, lo que produce una alta rapidez de aplicación de la carga. La rapidez de cambio de la aceleración está determinada por la tercera derivada del desplazamiento y recibe el nombre de “jalón” o “cheque”. Este “jalón” de magnitud infinita. La falta de rigidez y el juego de los engranajes en el sistema también tienden a aumentar el efecto de la carga de impacto. En el movimiento parabólico en que el “choque” es infinito, el impacto ocurre dos veces durante l ciclo y tiende el efecto de un golpe fuerte en el sistema que puede producir vibraciones indeseables además de provocar daños estructurales. C) MOVIMIENTO PARABÓLICO Tiene aceleración constante, es decir la velocidad aumenta uniformemente dura la primera mitad del movimiento y decrece en la segunda mitad. D) MOVIMIENTO CICLOIDAL El movimiento cicloidal se obtiene mediante la rodadura de una circunferencia de radio d/2π, en donde d es la elevación (o descenso) sobre el eje de ordenadas. CINEMÁTICA DE LEVAS a) Movimiento Uniforme La ecuación del movimiento de seguidor d será. y La velocidad será la derivada del movimiento con respecto al tiempo ýv d d dt La aceleración v d w ÿ = a = o. y= desplazamiento del seguidor (cm) ý= velocidad del seguidor (cm/s) ÿ= aceleración del seguidor (cm/s2) d= subida o elevación del seguidor (cm) = ángulo girado x la leva durante la subida. = wt= ángulo de la leva medido desde el comienzo de la subida. w= velocidad angular de la leva, rad/s t= tiempo (seg.). b) Movimiento Parabólico Tiene una discontinuidad en el punto de inflexión y se deben escribir dos grupos de ec. Para 0 /2 Y= c2 Ec. válida para el punto de inflexión Y=d/2 =/2 sustituyendo en la ec. Y= c2 d/2 = c(/2)2 c = 2d 2 2 De manera que : y 2d desplazamiento. p La velocidad ýv Aceleración ÿ a 4dw 2 4dw2 2 Para /2 < < Ec del movimiento y= C2+ C2 +C3 3 Condición y d D= C1+C2 + C3 2 También para = la v= o Ý = C2w + 2C3 w 0 = C2w + 2C3 w la máxima velocidad se presenta = /2 2dw C2 w 2C 3w / 2 dw 2C 3w C 3w C 3 / w Resolviendo el sistema 2 C 3 2d 4d ; C2 C1 d 2 y d 4d - 2d 2 2 4 2 2 2 = d 1 2 1 21 2 El desplazamiento y d 1 2 1 Velocidad ýv4 Aceleración ÿ a w 1 d 4dw2 2 c) Movimiento Armónico y d 2 1 Cos vý d aÿ 2 dw Sen 2 2 w Cos Salto: es la tercera derivada o segunda aceleración indica los cambios bruscos de la fuerza d) Movimiento Cicloidal Es uno de los mejores movimientos porque la aceleración es cero al principio y al fin de la subida. 1 2 y d Sen 2 vý dw 2 1 Cos 2 w 2 a ÿ 2d Sen ANGULO DE PRESIÓN El ángulo de presión es uno de los factores más importantes en la determinación del tamaño de la leva. En proyectos de máquinas el tamaño de la leva influye en la magnitud de las fuerzas y en las dimensiones de muchos otros elementos. Una leva grande no es deseable porque ocupa más espacio, produce más desequilibrio a altas velocidades y el seguidor tiene que recorrer un camino más largo. Por otra parte una leva pequeña tendrá mucha más pendiente y tenderá a fleccionar lateralmente al seguidor. (Es decir la leva pequeña tiene un mayor ángulo de presión). Si se ha de mantener un mismo ángulo de presión en diversas levas, cada una con movimiento diferente, el tamaño de la leva depende del movimiento utilizado. Circunferencia primitiva necesaria para dar el mismo ángulo de presión con diferentes movimientos básicos. A: Movimiento Uniforme. B: Uniforme Modificado C: Movimiento Armónico D: Movimiento Cicloidal E: Movimiento Parabólico. Los métodos matemáticos que relacionan el ángulo de presión con las dimensiones de la leva son muy complicados. Y por ello se emplean métodos aproximados. Coeficiente de la leva f l d f = Coeficiente de la leva l = Arco de la circunferencia primitiva d = Subida del seguidor Por ejemplo: El coeficiente de la leva para un movimiento uniforme y un ángulo de presión de 30º es 1.73 : ya que l 1.73 d l 1.73d f 1.73 d d El Coeficiente de la Leva: Es la longitud del arco de la circunferencia primitiva que subtiende el movimiento de subida (o vuelta) para aun ángulo de presión y tipo de movimiento; dado en múltiplos de la subida. Existen tablas del valor de f para diferentes ángulos y movimientos . La longitud del arco de circunferencia primitiva. l rp y por tanto el radio de la circunferencia primitiva rp l fd COEFICIENTE DE LA LEVA PARA MOVIMIENTOS BÁSICOS Angulo de Presión uniform e 10 5.67 15 3.73 20 2.75 25 2.14 30 1.73 35 1.43 40 7.19 45 1 Tipo de Movimiento Uniforme Armónico Modificado Simple 5.84 3.99 3.10 2.58 2.27 2.06 1.92 1.83 8.91 5.85 4.32 3.36 2.72 2.24 1.87 1.57 Parabólico y Cicloidal 11.34 7.46 5.50 4.28 3.46 2.86 2.38 2.00 Teóricamente el ángulo de presión varía entre 10º y 45º En la práctica los ángulos de presión mayores son del orden de 30º a 35º Un descentramiento del rodillo, disminuye o reduce el ángulo de presión, por esta razón el ángulo de presión no es un factor demasiado importante en el proyecto de levas. Lo mismo ocurre para seguidores de pie plano y los seguidores oscilantes. Ejemplo : Una leva de plato debe conducir un seguidor en movimiento de traslación elevándolo 2cm con movimiento cicloidal y ángulo de presión menor de 25º en 180º de rotación de la leva. El seguidor debe volver a la posición inicial con movimiento armónico simple y ángulo de presión menor de 35º tan rápidamente como sea posible. El seguidor llevará un rodillo de 1cm de diámetro. Determinar los radios de las circunferencias primitiva, base y principal y los ángulos de leva correspondientes al retorno y al periodo de reposo. Solución : El tamaño de la leva está determinado únicamente por el movimiento de elevación. Según tabla : con ¢ = 25º f 4.28 para movimiento cicloidal Radio de la circunferencia primitiva rp f.d 4.28 x 2 2.72 cm. Puesto que la circunferencia primitiva pasa por el centro del rodillo, en el punto medio de la elevación. El rodillo de la circunferencia principal es. d rA rp 2.72 1 1.72 cm. 2 El radio de la circunferencia base rB 1.72 1 1.22 cm. 2 Luego para el movimiento de retorno f 2.24 (movimiento armónico simple y ¢ = 35º). Se conoce también el rodillo de la circunferencia primitiva entonces el ángulo de la leva que corresponde al periodo de retorno,. Será: º fd 2.24 x 2 180 1.65 rad . ó 1.65 x 95º rp 2.72 El ángulo correspondiente para el periodo de reposo 360º - 180º – 95º -= 75º Ejemplo # 2 una leva armónica tiene un círculo de base con un rodillo de 1.5 cm y el seguidor 0.5 cm y una carrera de 0.8 cm. La elevación se produce en una rotación de 90º el descentramiento del seguidor con respecto al eje de la leva es 0.6 cm. Calcular los valores del rodillo r para la superficie primitiva para las posiciones angulares de 0º, 15º, 30º, 45º, 60º, 75º, 75º y 90º. ¿Cuál es el máximo valor de la aceleración si la leva gira a 600 rpm? yo ro e2 ro rbase rsegidor 2 cm. 2 2 r 2 ( yo x)2 e2 ro e2 2 yo x x2 x2 e 2 ro 2 yo x x2 2 90º 2 2 Es el mov. Armónico yo 22 0.62 1/ 2 X d 2 1 Cos 1.9079 r 2 4 3.81575 x x 2 2 0º 15º 30º 45º 60º 75º 90º 0º 30º 60º 90º 120º 150º 180º Cos 1 – Cos 1 0.866 0.5 0 -0.5 -0.866 1 0 0.1340 0.5 1 1.5 1.866 2 X 0 0.0536 0.2 0.4 0.6 0.7464 0.8 w La aceleración ya 3.815 5 X 0 0.20452 0.76315 1.5263 2.2895 2.8481 3.0526 X2 0 2.873x10-3 0.04 0.16 0.36 0.5571 0.64 2 20 60 2 d w2 Cos 2 2 La aceleración es mal cuando Cos 1 2 d w2 2 . 0.8 . 400 2 a 6316.547 cm / seg 2 63.16 m 2 2 2 s 2 2 4 r2 4 4.2074 4.803 5.6863 6.6495 7.4052 7.6926 r 2 2.05 2.192 2.3846 2.5786 2.7212 2.7736 FUERZA EN LAS LEVAS La fig. ilustra un sistema típico de leva y seguidor de rodillo. el seguidor es retenido contra la leva muelle de retenida y también mediante una fuerza P, (que puede se + o – y también función del tiempo). La masa combinada del seguidor completo y una carga combinada puede considerarse en muchos problemas, como una carga concentrada. Para una aceleración hacia abajo AA actúa hacia arriba una fuerza de inercia –m4 AA. Fs = Fuerza del muelle (depende de la comprensión inicial del muelle, así como del desplazamiento del seguidor). F34 = Fuerza del rodillo contra el seguidor, está inclinada un ángulo igual al de presión, y por ello tiene una componente horizontal que tiende a flexar el seguidor. Este componente la resisten las fuerzas normales en los cojinetes Ne y ND; si existe rozamiento se obtiene unas fuerzas totales FB14, FD.14 T2 = par para mover la leva (proporcionado por una fuente de energía o una volante). Es posible desarrollar una relación sencilla entre el par y la velocidad del seguidor en una excéntrica con seguidor de traslación. P. = Centro instantáneo de rotación, común a leva y al seguidor. El ángulo de presión ¢ es el formado por las rectas A02 y AP. La velocidad del seguidor es por tanto. Ý = w a tg ¢ 1 Si llamamos F23y a la componente vertical de la resultante de las fuerzas del seguidor que actúan sobre la leva. el par es: T2 F32 (a tg ¢) y 2 Luego despejando a tg ¢ de 1 y sustituyendo en (2) T2 ý y F32 w Ejemplo: Una excéntrica mueve un seguidor radial de traslación con movimiento cicloidal a 1200 r.p.m. Las carreras de subida y vuelta son de 120º cada una, con dos descansos iguales. El seguidor se mantiene en contacto con la leva por un muelle de compresión de 0.625 cm. para proporcionar una carga inicial. Calcular la componente radial de la fuerza de la leva durante la subida y el par en el eje de la leva para subida de 2.5cm y 0.9 kg de masa del seguidor. 120º ó 2.09 Rad . d= 2.5 cm Por ejemp. Para 80º ó 1.396 Rad . w 2 2. 120 125.66 Rad s. 60 60 para movimiento cicloidal: y d ý 1 2 1 2 . 1.396 1.396 Sen Sen 2.01 cm. 2.5 2.09 2.09 2 2 dw 2 2.5 . 125.66 2 . 1.396 1 Cos 1 Cos 225.47 cm s 2.09 2 . 09 2 w 2 2 1.396 125.66 ÿ 2 d Sen 2 x 2.5 x 49,176 cm 2 Sen s 2.09 2.09 2 La fuerza de inercia 0.9 m4 ÿ 49.176 45.2 Kg. 980 La compresión inicial del muelle es 0.625 cm. Por tanto. Fs k yo y 30 0.625 2.01 79.05 Kg. Debido a que el muelle actúa hacia abajo. - La fuerza total radial (vertical) que actúa sobre la leva es la suma de las fuerzas del muelle y de la inercia; por que no se ha especificado una carga externa y se ha despreciado el rozamiento F32 Fs m4 ÿ 79.05 45.2 33.85 Kg. y El par se calcula T2 ý 225.47 F 32 y 33.85 60.74 kg cm. w 125.66 Angulo de La leva En grados 0º 10º 20º 30º 40º 50º 60º 70º 80º 90º 100º 110º 120º Desplaz. y (Cm) Velocidad y (cm/s) Velocidad s ÿ cm Fza de Inercia m4ÿ (kg) Fza Del muelle Fs (kg) Fza result. Fy32 (kg) Par en el Eje T2 Km – cm