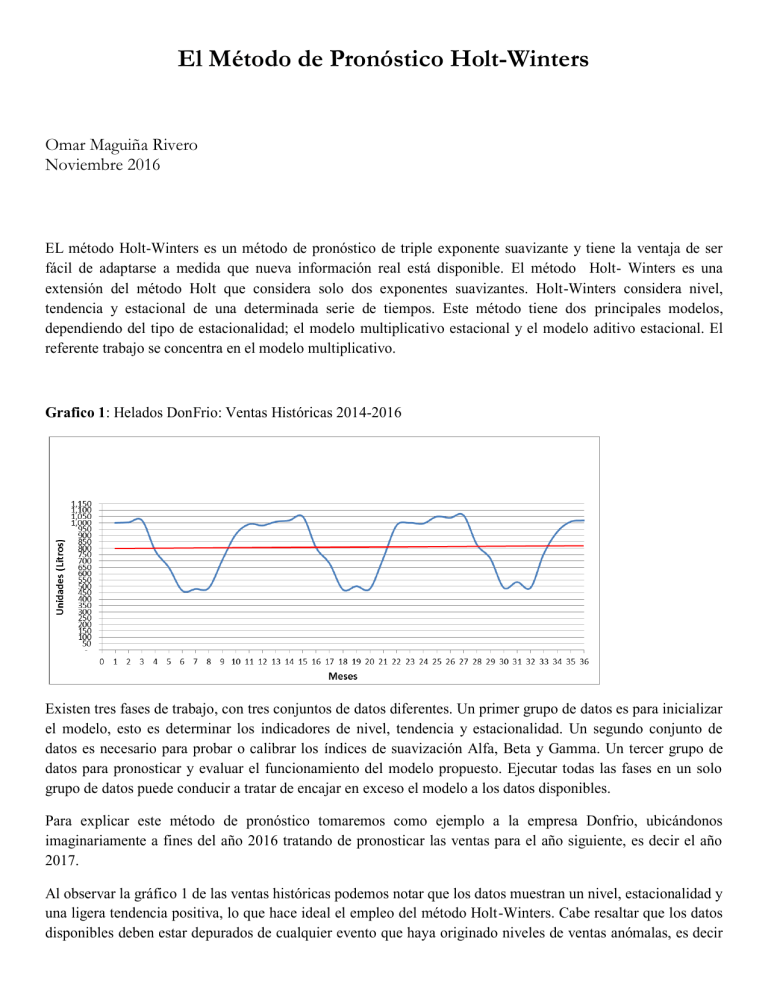
El Método de Pronóstico Holt-Winters Omar Maguiña Rivero Noviembre 2016 EL método Holt-Winters es un método de pronóstico de triple exponente suavizante y tiene la ventaja de ser fácil de adaptarse a medida que nueva información real está disponible. El método Holt- Winters es una extensión del método Holt que considera solo dos exponentes suavizantes. Holt-Winters considera nivel, tendencia y estacional de una determinada serie de tiempos. Este método tiene dos principales modelos, dependiendo del tipo de estacionalidad; el modelo multiplicativo estacional y el modelo aditivo estacional. El referente trabajo se concentra en el modelo multiplicativo. Grafico 1: Helados DonFrio: Ventas Históricas 2014-2016 Existen tres fases de trabajo, con tres conjuntos de datos diferentes. Un primer grupo de datos es para inicializar el modelo, esto es determinar los indicadores de nivel, tendencia y estacionalidad. Un segundo conjunto de datos es necesario para probar o calibrar los índices de suavización Alfa, Beta y Gamma. Un tercer grupo de datos para pronosticar y evaluar el funcionamiento del modelo propuesto. Ejecutar todas las fases en un solo grupo de datos puede conducir a tratar de encajar en exceso el modelo a los datos disponibles. Para explicar este método de pronóstico tomaremos como ejemplo a la empresa Donfrio, ubicándonos imaginariamente a fines del año 2016 tratando de pronosticar las ventas para el año siguiente, es decir el año 2017. Al observar la gráfico 1 de las ventas históricas podemos notar que los datos muestran un nivel, estacionalidad y una ligera tendencia positiva, lo que hace ideal el empleo del método Holt-Winters. Cabe resaltar que los datos disponibles deben estar depurados de cualquier evento que haya originado niveles de ventas anómalas, es decir EL MÉTODO DE PRONÓSTICO HOLT-WINTERS ventas que no se espera se repitan en el futro, como incremento de ventas por promociones realizadas en el pasado. En el cuadro 1 tenemos ventas históricas que completan tres estaciones de la empresa DonFrio (20142016), las cuales emplearemos para demostrar el uso de la técnica Holt-Winters Nivel de ventas (a), tendencia (b) y factores de estacionalidad (f) Para determinar el nivel actual de ventas (promedio), existen diversas técnicas. Emplearemos el método de promedio móvil, debido a que este método es uno de los que mejor reflejan la existencia de tendencias al alza o baja. El en grafico 1 observamos que cada estación está compuesta de doce periodos (de enero a diciembre). Es decir la curva que forman los niveles de ventas tiende a repetirse cada doce meses. Cuadro 1: Ventas Históricas Año 1 2014 2015 2016 Mes 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 3 Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Omar Maguiña Rivero Ventas -Datos Históricos 4 Promedio móvil 5 1,000 1,005 1,020 780 650 468 480 490 710 910 990 980 1,010 1,020 1,050 805 680 475 502 480 720 980 1,000 995 1,050 1,040 1,060 829 720 490 535 489 760 930 1,010 1,020 790.25 791.08 792.33 794.83 796.92 799.42 800.00 801.83 801.00 801.83 807.67 808.50 809.75 6 790.25 791.08 792.33 794.83 796.92 799.42 800.00 801.83 801.00 801.83 807.67 808.50 809.75 Promedio Factor de móvil centrado estacionalidad inicial 7 8 791.19 1.26392 791.19 1.27024 791.19 1.28920 791.19 0.98586 791.19 0.82155 791.19 0.59151 790.67 0.60708 791.71 0.61891 793.58 0.89468 795.88 1.14339 798.17 1.24034 799.71 1.22544 800.92 1.26105 801.42 1.27274 801.42 1.31017 804.75 1.00031 808.09 0.84149 809.13 0.58705 808.61 0.62082 808.61 0.59361 808.61 0.89042 808.61 1.21196 808.61 1.23669 808.61 1.23051 EL MÉTODO DE PRONÓSTICO HOLT-WINTERS Para iniciar el modelo vamos a trabajar únicamente con los datos correspondientes a los años 2014 y 2015; dejamos el año 2016 para calibrar nuestro modelo. Las cuatro primeras columnas del cuadro 1 son para indicar el año, período, mes y demanda histórica en unidades, información que debe ser proporcionada para nuestro trabajo de pronóstico. En las columnas 5 y 6 se muestran los cálculos del promedio móvil, el cual debe ser “centrado” en la columna 7. El promedio móvil de la demanda de los doce primeros meses (columna 4; períodos 1, 2, 3… 12) es 790.25 unidades; lo ubicamos en junio 2014 y repetimos la misma cifra en julio 2014. Esto debido a que 12 representa un número par sin centro, esto no ocurriría si se tratase de una estación con un número impar de períodos. El segundo promedio móvil de la demanda de doce meses (períodos 2, 3, 4…13) es de 791.08 unidades; lo ubicamos frente a los meses de julio 2014 y agosto 2014. El tercer promedio móvil, (períodos 3, 4, 5…14) lo ubicamos frente a los meses de agosto 2014 y septiembre 2014. Repetimos la operación hasta el promedio móvil décimo tercero (períodos 13, 14, 15…24) y ubicamos el resultado de 809.75 frente a los meses de junio 2015 y julio 2015). El siguiente paso es obtener los promedios móviles por mes (columna 7), empezamos por el mes de julio del 2014 con 790.67 [(791.08 + 790.25)/2], luego sigue agosto del 2014 con 791.71 [(792.33 + 791.08)/2] y así sucesivamente hasta junio del 2015 con 809.13 [(809.75 + 808.50)/2]. Los meses de enero a junio del 2014 son completados promediando los dos primeros meses disponibles, en este caso con los datos de julio y agosto con 791.19 [(790.67 + 791.71)/2]. Para los meses de julio a diciembre del 2015 son completados promediando los dos últimos meses disponibles, en este caso con los datos de mayo y junio con 808.61 [(808.08 + 809.13)/2] (Nahmias Steven, 2009). La columna 8 del cuadro 1 se refiere a los factores de estacionalidad inicial por período, para lo cual dividimos las ventas reales de cada mes entre el promedio móvil centrado obtenido en el paso anterior. Así para el mes de enero de 2014 tenemos un factor de estacionalidad de 1.26392 (1,000/791.19). Para el mes de febrero del 2014 tenemos un factor de estacionalidad de 1.27024 (1,005/791.19) y así sucesivamente para cada mes de los años 2014 y 2015. Cuadro 2: Factor de estacionalidad normalizado Mes Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Total Promedio de factores mensuales 1.26249 1.27149 1.29969 0.99309 0.83152 0.58928 0.61395 0.60626 0.89255 1.17768 1.23852 1.22798 12.00447 Omar Maguiña Rivero Factor de estacionalidad normalizado 1.26201 1.27102 1.29920 0.99272 0.83121 0.58906 0.61372 0.60603 0.89222 1.17724 1.23805 1.22752 12.00000 EL MÉTODO DE PRONÓSTICO HOLT-WINTERS Como disponemos de factores de estacionalidad para dos años (2014 y 2015), procedemos a promediar los factores de igual período, es decir el promediamos el factor de estacionalidad inicial del mes de enero del 2014 con el factor de estacionalidad inicial del mes de enero del 2015, lo cual nos da un factor promedio de 1.26249 [(1.26392 + 1.26105) / 2] ; luego promediamos el factor de estacionalidad inicial del mes de febrero del 2014 con el factor de estacionalidad inicial del mes de febrero del 2015, lo cual nos da un factor promedio de 1.27149 [(1.27024 + 1.27274) / 2] y así sucesivamente todos los períodos del año 2014 y 2015, como se aprecia en el cuadro 2. La sumatoria de los factores iniciales debe sumar P (Número de períodos de la estacionalidad) en este caso 12, de no ser así procedemos a normalizarlo o ajustarlo para que sumen exactamente 12, multiplicando cada promedio de factor mensual por 12/12.00447. Al resultado obtenido lo llamamos factores de estacionalidad normalizados. Los factores de estacionalidad normalizado representan la estacionalidad esperada de las ventas futuras de la empresa. Las cifras superiores a uno, representan periodos cuyas ventas esperadas son superiores al promedio anual. Las cifras inferiores a uno, representan periodos cuyas ventas esperadas son inferiores al promedio anual. Cuadro 3: Demanda Desestacionalizada Año 1 2014 2015 Mes 2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 3 Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Omar Maguiña Rivero Ventas -datos Factor de Nivel históricos estacionalidad demanda desnormalizado estacionalizada 4 6 5 1,000 1.26201 792.39 1,005 1.27102 790.70 1,020 1.29920 785.10 780 0.99272 785.72 650 0.83121 781.99 468 0.58906 794.49 480 0.61372 782.12 490 0.60603 808.54 710 0.89222 795.77 910 1.17724 772.99 990 1.23805 799.64 980 1.22752 798.36 1,010 1.26201 800.31 1,020 1.27102 802.51 1,050 1.29920 808.19 805 0.99272 810.90 680 0.83121 818.08 475 0.58906 806.37 502 0.61372 817.96 480 0.60603 792.04 720 0.89222 806.98 980 1.17724 832.46 1,000 1.23805 807.72 995 1.22752 810.58 EL MÉTODO DE PRONÓSTICO HOLT-WINTERS En el cuadro #3 mostramos como se determina los niveles de demanda desestacionalizada que nos permitirán determinar la tendencia empleando la técnica de los mínimos cuadrados. La demanda desestacionalizada para cada periodo se obtiene dividiendo la demanda de cada periodo por el factor de estacionalidad normalizado correspondiente. Así para el período 1 el nivel de demanda desestacionalizada es de 792.39 unidades (1,000/1.26201), para el segundo período es de 790.70 unidades (1,005/1.27102) y así sucesivamente. Una vez obtenido las demandas desestacionalizadas para los periodos del 1 al 24, podemos proyectar los períodos siguientes y luego re-estacionalizarla empleando los factores de estacionalidad normalizado correspondientes. La demanda desestacionalizada representa el promedio mensual de las ventas anualizadas en cada período. Cuadro 4: Establecimiento del nivel y tendencia empleando mínimos cuadrados 2014-2015 X 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 300 Y 792.39 790.70 785.10 785.72 781.99 794.49 782.12 808.54 795.77 772.99 799.64 798.36 800.31 802.51 808.19 810.90 818.08 806.37 817.96 792.04 806.98 832.46 807.72 810.58 19,201.91 Omar Maguiña Rivero X^2 1.00 4.00 9.00 16.00 25.00 36.00 49.00 64.00 81.00 100.00 121.00 144.00 169.00 196.00 225.00 256.00 289.00 324.00 361.00 400.00 441.00 484.00 529.00 576.00 4,900.00 Y^2 627,881.91 625,206.49 616,382.01 617,355.92 611,508.36 631,214.36 611,711.69 653,736.93 633,249.89 597,513.54 639,424.13 637,378.69 640,496.10 644,022.30 653,171.08 657,558.81 669,254.89 650,232.58 669,058.56 627,327.36 651,216.72 692,989.65 652,411.60 657,039.94 15,367,343.50 X.Y 792.39 1,581.40 2,355.30 3,142.88 3,909.95 4,766.94 5,474.84 6,468.32 7,161.93 7,729.90 8,796.04 9,580.32 10,404.03 11,235.14 12,122.85 12,974.40 13,907.36 14,514.66 15,541.24 15,840.80 16,946.58 18,314.12 18,577.56 19,453.92 241,592.87 EL MÉTODO DE PRONÓSTICO HOLT-WINTERS A continuación empleamos la técnica de mínimos cuadrados para proyectar la demanda desestacionalizada para el año 2016; donde Y representa la demanda desestacionalizada obtenida del cuadro 3 y X representa el periodo de análisis (2014-2015). La fórmula empleada para obtener los parámetros a y b de mínimos cuadrados es: 𝑎= ∑ 𝑋 2 . ∑ 𝑌 − ∑ 𝑋 . ∑ 𝑋. 𝑌 𝑁. ∑ 𝑋 2 − (∑ 𝑋)2 𝑏= 𝑁. ∑ 𝑋. 𝑌 − ∑ 𝑋 . ∑ 𝑌 𝑁. ∑ 𝑋 2 − (∑ 𝑋)2 Resolviendo obtenemos un nivel (a) de 783.03 unidades y una tendencia (b) de 1.3643 unidades. Estos parámetros se emplearan para pronosticar nuestra demanda 2016 en el siguiente cuadro. Cuadro 5: Pronostico de la demanda Año 1 2016 Mes 2 24 25 26 27 28 29 30 31 32 33 34 35 36 Ventas históricas 3 Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre 4 Nivel Tendencia 5 1,050 1,040 1,060 829 720 490 535 489 760 930 1,010 1,020 9,933 815.77 824.72 822.28 819.78 828.23 848.43 841.28 857.87 833.31 843.47 817.14 816.67 824.14 6 1.3643 1.7662 1.5433 1.3290 1.7064 2.6866 2.1653 2.9298 1.4728 1.9332 0.4353 0.3873 0.7627 Factor de Pronóstico estacionalidad 2016 ajustado 7 8 1.26312 1.27040 1.29858 0.99354 0.83295 0.58840 0.61471 0.60411 0.89310 1.17333 1.23792 1.22853 11.99869 1,031 1,050 1,070 815 690 501 518 522 745 995 1,012 1,003 9,952 (19) -0.19% En el cuadro 5, realizamos el pronóstico de la demanda para el período 2016, período ya ejecutado. Es decir, empleamos los parámetros obtenidos, con datos trabajados de los años 2014 y 2015, para comprobar que se ajustan razonablemente al año 2016 y de ser necesario se ajustarán con los factores de ajuste alfa, gama y beta para el nivel, tendencia y estacionalidad respectivamente. Omar Maguiña Rivero EL MÉTODO DE PRONÓSTICO HOLT-WINTERS Uno de los aspectos más discutidos de este método es cómo inicializar el modelo, es decir cuál será el primer dato del nivel y tendencia (período 25). En este ejemplo emplearemos los datos obtenidos de nuestra proyección con mínimos cuadros. La fórmula general del pronóstico es: D t, t+1 = (at +T.bt) + F t+T-P Dónde: D = Demanda o variable a estimar; a = Nivel promedio de ventas; b = Tendencia; F = Factor de estacionalidad; t = Período actual; T = Número de períodos en adelante que se desea proyectar Para este ejemplo tomaremos los siguientes valores: alfa: 0.5100; beta: 0.053; gamma: 0.10. Ubicándonos en diciembre del 2015 procedemos a pronosticar la demanda para el año 2016. Como valores iniciales de nivel (a0) empleamos 815.77 (783.03 + 24 x 1.3643) unidades y para la tendencia (b0) 1.3643 unidades. Como factores de estacionalidad inicial emplearemos los factores de estacionalidad normalizados2015 calculados anteriormente. Empleando la formula modelo de pronóstico para el mes de enero del 2014 la demanda para el mes de enero del 2016 se estima en 1031 unidades [(815.77 + 1.3643) x 1.26201]. Una vez inicializado el pronóstico, para el resto de meses debemos primero actualizar el nivel, la tendencia y los factores de estacionalidad conforme se conocen los datos reales. Para actualizar el nivel consideramos la siguiente fórmula: Nivel-0 = Alfa x (Demanda-0 / Factor de estacionalidad-p) + (1 - Alfa) x (Nivel-1 + Tendencia-1) Para actualizar la tendencia consideramos la siguiente fórmula: Tendencia-0 = Beta x (Nivel-0 - Nivel-1) + (1 - Beta) x (Tendencia-1) Para actualizar los factores de estacionalidad consideramos la siguiente fórmula: Factor de estacionalidad-0 = Gamma x (Demand-0 / Level-0) + (1 - Gama) x (Factor de estacionalidad-P) Omar Maguiña Rivero EL MÉTODO DE PRONÓSTICO HOLT-WINTERS Note que en cada una de las formulas presentadas la primera parte incide en los datos más recientes, mientras que la segunda parte incide en la parte histórica. Los factores de suavización alfa (α), beta (β) y gamma (γ) varían entre 0 y 1. Asignar el valor de cero significa que la nueva información (último dato real) es meramente accidental y el patrón de comportamiento de las ventas debe mantener los niveles, tendencias o factores de estacionalidad históricos-dependiendo a cuál factor suavizante se asigne el valor de cero. Por otro lado, asignarle un valor de uno a estos factores, significa asegurar que el último nivel de ventas alcanzado en el período es relevante, estableciéndose así un nuevo nivel, tendencia o estacionalidad en las ventas. Para el mes de enero del 2016 el nuevo nivel queda ajustado en 824.72 unidades [0.51 x (1,050 / 1.26201) + (10.51) x (815.77 + 1.3643)], la tendencia queda ajustada a 1.7662 unidades [0.053 x (824.72 – 815.77) + (1 0.053) x 1.3643] y el factor de estacionalidad en 1.26312 [0.10 x (1,050 / 824.72) + (1 – 0.10) x 1.26201] Una vez actualizados los parámetros para el mes de enero podemos pronosticar febrero considerando la última información disponible. Ubicándonos en enero del 2016 aplicando la formula general del pronóstico tenemos para el mes de febrero de 1,050 unidades [(824.72 + 1.7662) x 1.27102]. Para el mes de febrero del 2016 el nuevo nivel queda ajustado en 822.28 unidades [0.51 x (1,040 / 1.27102) + (1-0.51) x (824.72 + 1.7662)], la tendencia queda ajustada a 1.5433 unidades [0.053 x (822.28 – 824.72) + (1 0.053) x 1.7662] y el factor de estacionalidad en 1.27040 [0.10 x (1,040 / 822.28) + (1 – 0.10) x 1.27102]. Con estos datos pronosticamos marzo con 1,070 unidades [(814.86 + 2.8384) x 1.29920]. Repetimos la operación para cada uno de los meses restantes del año 2016. Al final del cuadro podemos observar que el total de ventas anuales reales suma 9,933 unidades y nuestro pronóstico llega a 9,952 unidades, con una diferencia de -19 unidades que representa un porcentaje bastante aceptable de error 0.19% de no ser el caso debe modificarse los factores de ajuste alfa, beta y gama hasta obtener una variación menor al 4% ó 5% como regla empírica. Una vez logrado este ajuste podemos concluir que nuestros parámetros se encuentran debidamente calibrados y podemos prepararnos para el verdadero pronóstico del año 2017. Cuadro 6: Normalización de factores de estacionalidad 2016 Mes Factor de Factor de estacionalidad estacionalidad ajustado normalizado Enero 1.26312 1.26326 Febrero 1.27040 1.27054 Marzo 1.29858 1.29872 Abril 0.99354 0.99365 Mayo 0.83295 0.83304 Junio 0.58840 0.58846 Julio 0.61471 0.61478 Agosto 0.60411 0.60418 Septiembre 0.89310 0.89320 Octubre 1.17333 1.17346 Noviembre 1.23792 1.23806 Diciembre 1.22853 1.22866 Total 11.99869 12.00001 Omar Maguiña Rivero EL MÉTODO DE PRONÓSTICO HOLT-WINTERS Ahora procedemos a normalizar los factores de estacionalidad ajustado para que el total sea igual a P (Número de períodos de la estacionalidad), en este caso 12. Cada factor de estacionalidad ajustado es multiplicado por (12 / 11.99869) La tercera columna del cuadro 6 muestra los resultados de la normalización. Cuadro 7: Establecimiento del nivel y tendencia empleando mínimos cuadrados 2014-2016 X 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 666 Y 792.39 790.70 785.10 785.72 781.99 794.49 782.12 808.54 795.77 772.99 799.64 798.36 800.31 802.51 808.19 810.90 818.08 806.37 817.96 792.04 806.98 832.46 807.72 810.58 832.01 818.24 815.89 835.08 866.21 831.83 871.73 806.89 851.81 789.98 815.80 830.94 29,168.32 Omar Maguiña Rivero X^2 1.00 4.00 9.00 16.00 25.00 36.00 49.00 64.00 81.00 100.00 121.00 144.00 169.00 196.00 225.00 256.00 289.00 324.00 361.00 400.00 441.00 484.00 529.00 576.00 625.00 676.00 729.00 784.00 841.00 900.00 961.00 1,024.00 1,089.00 1,156.00 1,225.00 1,296.00 16,206.00 Y^2 627,881.91 625,206.49 616,382.01 617,355.92 611,508.36 631,214.36 611,711.69 653,736.93 633,249.89 597,513.54 639,424.13 637,378.69 640,496.10 644,022.30 653,171.08 657,558.81 669,254.89 650,232.58 669,058.56 627,327.36 651,216.72 692,989.65 652,411.60 657,039.94 692,240.64 669,516.70 665,676.49 697,358.61 750,319.76 691,941.15 759,913.19 651,071.47 725,580.28 624,068.40 665,529.64 690,461.28 23,651,021.12 X.Y 792.39 1,581.40 2,355.30 3,142.88 3,909.95 4,766.94 5,474.84 6,468.32 7,161.93 7,729.90 8,796.04 9,580.32 10,404.03 11,235.14 12,122.85 12,974.40 13,907.36 14,514.66 15,541.24 15,840.80 16,946.58 18,314.12 18,577.56 19,453.92 20,800.25 21,274.24 22,029.03 23,382.24 25,120.09 24,954.90 27,023.63 25,820.48 28,109.73 26,859.32 28,553.00 29,913.84 545,433.62 EL MÉTODO DE PRONÓSTICO HOLT-WINTERS Para pronosticar el año 2017, iniciamos con el nivel y tendencia obtenida al pronosticar la demanda desestacionalizada esta vez incluyendo a los años 2014 al 2016. Así mismo emplearemos los factores de estacionalidad normalizados del año 2016. Siguiendo el enfoque de mínimos cuadrados para los datos de los años 2014 al 2016 obtenemos a = 782.52 y b = 1.498 Cuadro 8: Factores de estacionalidad normalizados 2016 Mes Factor de Factor de estacionalidad estacionalidad ajustado normalizado Enero 1.26312 1.26326 Febrero 1.27040 1.27054 Marzo 1.29858 1.29872 Abril 0.99354 0.99365 Mayo 0.83295 0.83304 Junio 0.58840 0.58846 Julio 0.61471 0.61478 Agosto 0.60411 0.60418 Septiembre 0.89310 0.89320 Octubre 1.17333 1.17346 Noviembre 1.23792 1.23806 Diciembre 1.22853 1.22866 Total 11.99869 12.00001 Para los periodos subsiguientes emplearemos la técnica de mínimos cuadrado proyectando el nivel y luego de agregar la tendencia y re-estacionalizarlo por período. Cuadro 9: pronóstico de ventas 2017 Año Mes Ventas históricas 36 2017 37 38 39 40 41 42 43 44 45 46 47 48 Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Omar Maguiña Rivero Nivel estimado 836.45 837.95 839.44 840.94 842.44 843.94 845.44 846.93 848.43 849.93 851.43 852.93 854.42 Tendencia 1.4980 1.4980 1.4980 1.4980 1.4980 1.4980 1.4980 1.4980 1.4980 1.4980 1.4980 1.4980 1.4980 Factor de Ventas estacionalidad pronóstico normalizado 2015 1.26326 1.27054 1.29872 0.99365 0.83304 0.58846 0.61478 0.60418 0.89320 1.17346 1.23806 1.22866 12.00001 1,059 1,067 1,092 837 703 498 521 513 759 999 1,056 1,050 10,152 EL MÉTODO DE PRONÓSTICO HOLT-WINTERS El nivel inicial (período 36) es a = [782.52 + 1.498 x 36)], la tendencia (b) se mantiene estable en 1.498 unidades por período y la estacionalidad como ya lo mencionamos serán los índices normalizados del año 2016. Así, el nivel para enero del 2017 es de 837.95 (782.52 + 1.498 x 37), para el mes de febrero del 2017 es de 839.44 (782.52 + 1.3643 x 38) y así sucesivamente hasta el período 48 correspondiente a diciembre del 2017. Una vez concluido con los cálculos de nivel procedemos pronosticar la demanda. Para enero del 2017 es de 1,059 unidades [(836.45 + 1.498) x 1.26326). Para el mes de febrero el pronóstico es de 1,067 unidades [(837.95 + 1.498) x 1.27054]. Para el mes de marzo la demanda se estima en 1,092 unidades [(839.44 + 1.498) x 1.29872]. Para el mes de abril tenemos un pronóstico de 837 unidades [(840.94 + 1.498) x 0.99365]. Esta operación se repite para cada período del año 2015. Ajustes mensuales al pronóstico 2017 Una de las ventajas del método Holt-Winters es poder ajustar el pronóstico a medida que los datos reales están disponibles. Cuadro 10: Actualización mensual de pronósticos. Año 2017 Mes 37 38 39 40 41 42 43 44 45 46 47 48 Enero Febrero Marzo Abril Mayo Junio Julio Agosto Septiembre Octubre Noviembre Diciembre Ventas históricas 1,102 1,150 1,151 850 750 Nivel estimado 836.45 855.49 881.99 885.98 872.22 887.92 Tendencia 1.4980 2.4278 3.7036 3.7188 2.7924 3.4765 Factor de Ventas estacionalidad pronóstico normalizado 2017 1.26575 1.27387 1.29876 0.99174 0.83420 1,059 1,090 1,114 852 715 505 Inicializamos enero del 2017 con un pronóstico de 1,059 unidades [(836.45+1.4980) x1.26326]. Una vez transcurrido el mes de enero del 2017 y conocidas sus ventas reales (1,102 unidades en el ejemplo) se estima el nuevo nivel, tendencia y estacionalidad para enero 2017. Con el nuevo nivel y tendencia de enero podemos pronosticar las ventas de febrero empleando el último factor de estacionalidad normalizado disponible del 2016 [(855.49+2.4278) x 1.27054]. Debe observarse que el factor de estacionalidad a emplearse es el último normalizado disponible, es decir el correspondiente al año anterior 2016. El pronóstico del mes de marzo se efectúa luego de conocidas las ventas reales de febrero y estimar su nuevo nivel, tendencia y estacionalidad. Así el nuevo pronóstico para marzo del 2017 que da establecido en 1150 unidades [(881.99+3.7036) x 1.29872]. La operación se repite para todos los periodos restantes del año 2017. El archivo en Excel desarrollado en este escrito puede ser encontrado en el siguiente link: https://drive.google.com/file/d/0B-UO-e1h0W-acnFwNEM3cTZJZGc/view?usp=sharing Omar Maguiña Rivero EL MÉTODO DE PRONÓSTICO HOLT-WINTERS BIBLIOGRAFÍA Caplice Chris (2014) Course: CTL.SC1x -Supply Chain & Logistics Fundamentals. USA: MIT-Center for Transportation & Logistics. Nahmias Steven (2009). Production and Operation Analysis 6th e. USA: McGraw Hill. Prajakta S. Kalekar (2004). Time series Forecasting using Holt-Winters Exponential Smoothing (04329008). Bombay: Kanwal Rekhi School of Information Technology. Schroeder Roger (2008) Operations Management; Contemporary Concepts and Cases. 4th e. USA: McGraw Hill. Omar Maguiña Rivero