Tarea Procesamiento Digital de Señales: Correlación, Convolución, DFT
Anuncio

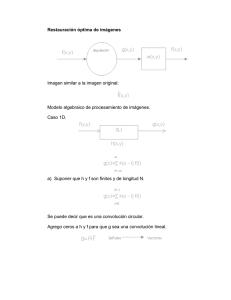
UNIVERSIDAD DEL BÍO-BÍO FACULTAD DE INGENIERÍA DEPARTAMENTO DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Tarea 1 Procesamiento Digital de Señales 410 143 Problema 1: Correlación La Fig. 1 muestra un radar que emite una señal xe(t) y recibe una señal xr(t) tal que la señal xr(t) es la señal enviada xe(t) con un retardo D una atenuación representada por α y ruido aditivo ω(n), es decir: xr t xe t D t l ña Se En la práctica, la señal recibida es altamente contaminada, por lo que el tratamiento de la señal no es sencillo y requiere de un procesamiento digital especial. a tid mi ns Tra da i ib ec lr ña Se De lo anterior, responda Fig. 1. Sistema Radar. justificadamente cada siguiente pregunta. a) Explique cómo se puede estimar D utilizando la herramienta la correlación ryx. Suponga una señal xe(t) = sin(ωt2) y una señal xr(t) = α∙sin(ω∙(t – DT)2) + σ2υ(t) (para la función υ(t) utilice en MatLab ‘randn()’), con ω = 2πf =2π∙200×103, D = 5, una varianza de σ2 = 0.05 y α = 0.5. Con esto grafique las señales xe(t) y xr(t) para 0 ≤ t ≤ 4×10-3 y T = 1/(8×103). b) Discretice las señales xe(t) y xr(t) con T = 1/(8×103) segundos y grafique nuevamente las señales de a). c) Grafique las señales xe(k) y xr(k) con 0 < k < 32 y la respectiva correlación ryx(k) entre -32 < k < 32. Use el gráfico para estimar el valor del retardo D. Para este caso desarrolle su propio algoritmo que obtenga la correlación. d) Repita c) para σ2 = 0.1 y para σ2 = 0.2. e) Repita c) considerando xe(t) = sin(ωkT), xr(t) = α∙sin(ω∙(kT – DT)) + σ2υ, con f = 1×103. f) Repita d) considerando xe(t) = sin(ωkT), xr(t) = α∙sin(ω∙(kT – DT)) + σ2υ, con f = 1×103. Problema 2: Convolución x k h k k p u kT El siguiente problema aborda la convolución discreta de un sistema determinado con una entrada x(k). Suponga que la función de transferencia está definida Fig. 2. Convolución. por: h(k) = kpαkTu(kT), con k ∈ [0, tend/T] y k kT y parámetros dados por T = 5/8, α = 0.8, tend = 15. Por otra parte, la entrada está dada por: x(k) = sin(2πfkT), con k ∈ [0, tend/T] Se pide responder justificadamente: a) Escriba la expresión de la convolución discreta para las funciones antes enunciadas. b) Desarrolle un código capaz de determinar la convolución considerando la señales antes dadas con f = 0.2 Hz. c) Repita b) pero con f = 0.1 Hz, compare su resultado al utilizar el comando de MatLab ‘conv()’. Profesor Jaime Rohten., Octubre 2019. UNIVERSIDAD DEL BÍO-BÍO FACULTAD DE INGENIERÍA DEPARTAMENTO DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Problema 3: DFT En este último problema, se debe utilizar la Transformada de Fourier Discreta: X k N 1 x n e j 2 kn / N , n 0 y la Transformada de Fourier Discreta inversa: 1 N 1 x n X k e j 2 kn / N . N k 0 Donde n representa el tiempo discreto y k el componente de frecuencia. Considere el sistema no lineal compuesto por un puente de diodos trifásico en la cual se ha sensado la corriente por la fase a, ia(n), el registro de la corriente se encuentra disponible en este link. Fig. 3. DFT. Se pide responder justificadamente: a) Escriba la definición de la Transformada de Fourier Discreta Ia(k) para la señal ia(n) y explique matemáticamente los pasos a seguir para desarrollar esta transformada. b) Realice su propio código para obtener la Transformada de Fourier Discreta. c) Grafique el módulo de la Transformada de Fourier Discreta, |Ia(k)|. d) Repita c) pero considerando el eje de las abscisas como la frecuencia, es decir k/(N×Ts), con Ts = 1/(51×50×4) segundos. e) Desde el gráfico en d) determine el valor de la señal para el armónico dado por 50 Hz y todos los múltiplos del mismo hasta la frecuencia 51×50 Hz. f) Calcule el THD de la señal de corriente donde el THD se define como: THD i a i 2 I a 50 iHz 51 2 I a 50Hz Fecha de Entrega 05 de Noviembre Importante ¿Cómo debo subir mi Tarea? 1. 2. 3. creo un .pdf con mi apellido y el de mi compañero ejemplo: ‘Rohten Wernekinck.pdf’ mis archivos .m, ejemplo ‘tarea.m’, “call_tarea.m”. junto todos los archivos en un .rar (ejemplo ‘Rohten Wernekinck.rar’) y lo subo a la plataforma. Profesor Jaime Rohten., Octubre 2019.