Parábola.

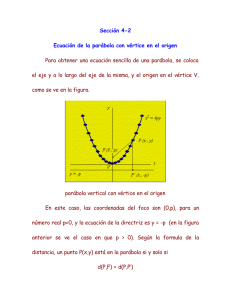
LA PARÁBOLA
Mgtr. Julio César Moreno Descalzi
jmoreno@usat.edu.pe
MATEMÁTICA BÁSICA
www.usat.edu.pe
www.usat.edu.pe
CONTENIDO
•
•
•
•
•
•
2
LA PARÁBOLA.
ECUACIONES DE LA PARÁBOLA.
DEDUCIÉNDO LA ECUACIÓN DE LA PARÁBOLA.
EJERCICIOS RESUELTOS.
PROBLEMA DE APLICACIÓN REAL.
EJERCICIOS PARA RESOLVER.
www.usat.edu.pe
LA PARÁBOLA
www.usat.edu.pe
LA PARÁBOLA
www.usat.edu.pe
ECUACIONES DE LA PARÁBOLA
Ecuación Ordinaria o Canónica de la Parábola:
La Parábola cuyo centro está en (0,0) y cuyo eje focal coincide con uno
de los ejes coordenados, tiene por ecuación:
x 2  4 py
y 2  4 px
Eje focal = Eje y
Eje focal = Eje x
La Parábola cuyo vértice es el punto (h,k) y su eje es paralelo al eje y,
tiene por ecuación:
x  h 2  4 p y  k 
 y  k 2  4 px  h 
Si p > 0, la parábola se abre hacia arriba, si p < 0, la parábola se abre hacia abajo.
Ecuación General de la Parábola:
Ax  Bx  Cy  D  0
2
www.usat.edu.pe
Ay 2  Bx  Cy  D  0
DEDUCIENDO LA ECUACIÓN
Por definición de parábola, tenemos:
d ( P, F )  d ( P, R )
x  02   y  a2  x  x2   y  a2
Elevando al cuadrado ambos miembros, se
obtiene:
x2   y  a   y  a
2
2
x 2  y 2  2ay  a 2  y 2  2ay  a 2
x 2  2ay  2ay
De donde:
x 2  4ay
............. Ecuación ordinaria de la Parábola
www.usat.edu.pe
ECUACIONES DE LA PARÁBOLA
x 2  4ay
x 2  4ay
Directriz : y = - a
www.usat.edu.pe
Directriz : y = a
ECUACIONES DE LA PARÁBOLA
y 2  4ax
y 2  4ax
Directriz : x = - a
www.usat.edu.pe
Directriz : x = a
EJERCICIOS RESUELTOS
Obtener la ecuación de la parábola con vértice en el origen y
cuya directriz es y=2
Solución: Como se observa en el gráfico la ecuación de la
parábola tiene la forma:
x 2  4 py
Como p=2, entonces la ecuación de
la parábola es:
x 2  8 y
www.usat.edu.pe
EJERCICIOS RESUELTOS
Hallar la ecuación de la parábola cuya directriz es la recta x=-6 y
su foco es F(0,0)
Solución: Graficando y ubicando los elementos en la ecuación
de forma:
 y  k 2  4 px  h 
Como la directriz está en x=-6, entonces:
V  (3,0)
y
F
Reemplazando, tenemos:
p  FV  3
y 2  4(3)x  3
y 2  12 x  36
www.usat.edu.pe
EJERCICIOS RESUELTOS
Dada la ecuación de la parábola x2 + 8y – 2x = 7 . Hallar su
vértice y su eje.
Solución: Completando cuadrados en la ecuación dada:
x2  8 y  2x  7
x 2  2 x  1  8 y  7  1
x  1  8 y  8
x  12  8( y  1)
2
Luego las coordenadas del vértice de la parábola es:
La ecuación de su eje es:
www.usat.edu.pe
x 1
V  (1,1)
EJERCICIOS RESUELTOS
Hallar la ecuación de la parábola cuyo vértice es el punto
(3,4) y cuyo foco es el punto (3,2).
Solución: Como el vértice V y el foco F de una parábola están sobre
su eje, y como en este caso cada uno de los puntos tiene
la misma abscisa 3, se sigue que el eje de la parábola es
paralelo al eje y.
Entonces la ecuación de la parábola es de la forma:
Reemplazando:
x  k 2  4 p y  k 
x  32  4 p y  4
Es una parábola que se abre hacia abajo y p es negativo:
Note que : p  2 y p  2
www.usat.edu.pe

x  32  8 y  4
APLICACIÓN
Puente Juscelino Kubitschek, Brasilia, Brasil. Los
arcos no se encuentran en el mismo plano y los cables
de suspensión forman una superficie parabólica
Golden Gate Bridge, uno de los más famosos, y
récord de longitud del vano central durante muchos
años. San Francisco (California)
www.usat.edu.pe
PARA RESOLVER
Los cables del tramo central de un puente colgante
tienen la forma de una parábola. Si las torres tienen
una separación de 800 metros y los cables están
atados a ellas 400 metros arriba del piso del puente,
¿qué longitud debe tener el puntal que está a 100
metros de la torre? Suponga que el cable toca el piso
en el punto medio del puente.
Determinar, en forma reducida, las ecuaciones de las siguientes
parábolas, indicando el valor del parámetro, las coordenadas del foco
y la ecuación de la directriz.
a) 6 y 2  12 x  0
b) 15x 2  42 y
Calcular las coordenadas del vértice y del foco, y la ecuación de la
directriz de las parábola: y2-6y-8x+17=0
Un cohete de juguete se dispara hacia arriba con una velocidad v0 (en pies/s)
y su altura h(t) sobre el piso en pies, después de t segundos, está dada por
h(t)=-16t2+v0t. a) El cohete llega al suelo después de 12 segundos ¿cuál es la
velocidad inicial v0? b) ¿cuál es la altura máxima alcanzada por el cohete?
www.usat.edu.pe
Mgtr. Julio César Moreno Descalzi
jmoreno@usat.edu.pe
http://www.facebook.com/usat.peru
https://twitter.com/usatenlinea
https://www.youtube.com/user/tvusat
https://plus.google.com/+usateduperu
www.usat.edu.pe