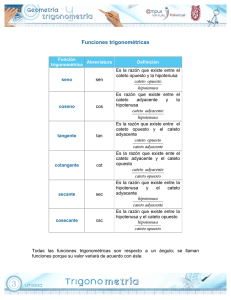
Activando proyección…………………………. COLEGIO JOSE ANTONIO GALAN MATEMATICAS, GRADO DECIMO PROFESOR: FREDY RODRIGUEZ DEFINICION El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos. Si un triángulo rectángulo tiene catetos de longitudes a y b , y la medida de la hipotenusa es c , se establece que: c a b Matemáticas 2 2 a +b =c 2 Grado Décimo HISTORIA El Teorema de Pitágoras lleva este nombre porque su descubrimiento recae sobre la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros, pero no ha perdurado ningún documento que exponga teóricamente su relación. Matemáticas Grado Décimo HISTORIA El Teorema de Pitágoras es de los que cuentan con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración de él para alcanzar el grado de Magíster matheseos. Matemáticas Grado Décimo EJEMPLO Encontrar el valor de la hipotenusa a= Solución: b= c=? En este triángulo nos están dando el valor de los catetos y debemos hallar el valor de la hipotenusa. Para el triángulo se tiene que a = 40 y b = 9 Aplicando el Teorema de Pitágoras: a2 + b2 = c2 40 2 + 92 = c 2 1600 + 81 = c 2 1681 = c 2 Y de aquí que: 1681 = c 41 = c Matemáticas Grado Décimo EJEMPLO Encontrar el valor del cateto b de la figura: Aplicando el Teorema de Pitágoras: a2 + b2 = c2 5 2 + b 2 = 40 2 b 2 = 40 2 − 5 2 c = 40 b=? b 2 = 1600 − 25 b 2 = 1575 Y de aquí que: b = 1575 a=5 b = 39,7 EJERCICIO 1 Hallar el valor de la hipotenusa del siguiente triángulo rectángulo: c= . a = 7 cm ? b = 12 cm EJERCICIO 2 Hallar el valor del cateto b del triángulo rectángulo: a = 36,2 cm c= 65, 3 b=? cm EJERCICIO 3 Halla la altura de un triángulo isósceles cuyos Lados miden c = 5 cm. y a = b = 4 cm. a = 4 cm . b h c = 5 cm. = 4 cm . EJERCICIO 4 El tamaño de las pantallas de televisión viene dado por la longitud en pulgadas de la diagonal de la pantalla (una pulgada equivale a 2,54 cm). Si un televisor mide 34,5 cm de base y 30 cm de altura, ¿cuál será su tamaño? 34,5 cm. d 30 cm. RAZONES TRIGONOMETRICAS Sea ABC, un triángulo rectángulo: A β El lado AC es el cateto opuesto al ángulo θ y el cateto adyacente al ángulo β c b θ C a B El lado AB es la hipotenusa El ángulo C mide 90º Matemáticas El lado BC es el cateto opuesto al ángulo β y el cateto adyacente al ángulo θ Los ángulos agudos θ y β son complementarios m∠θ + m∠β = 90º Grado Décimo RAZONES TRIGONOMETRICAS Se llaman Razones trigonométricas o Relaciones trigonométricas, a la razón (cociente) existente entre los lados de un triángulo rectángulo. Las seis relaciones trigonométricas para el ángulo θ se definen por: A Seno θ = Sen θ = β c b C Coseno θ = Cos θ = a θ Cotangente θ = Cot θ = B Tangente θ = Tan θ = Cateto adyacente Cateto opuesto Secante θ = Sec θ = a = b Hipotenusa Cateto adyacente = Matemáticas Cateto adyacente Hipotenusa Cateto opuesto Cateto adyacente = Hipotenusa Cateto opuesto = a c b a c a Cosecante θ = Csc θ = b = c Cateto opuesto Hipotenusa = c b Grado Décimo EJERCICIO 1 Halla las relaciones trigonométricas para el ángulo β de la figura anterior : A β b = 13,5 C c = 45,3 a = 21,2 Matemáticas B Grado Décimo EJERCICIO 2 Construya cada uno un triángulo rectángulo donde el ángulo θ = 60º y halle cada una de las relaciones trigonométricas del ángulo θ Matemáticas Grado Décimo EJERCICIO 3 Los triángulos ABC y ADE son rectángulos con el ángulo α común a los dos triángulos. Hallar el valor de las razones trigonométricas del ángulo α C 39 E 15 13 5 B α D 36 Matemáticas 12 A Grado Décimo EJERCICIO 4 Hallar el valor de las razones trigonométricas para el ángulo β del siguiente triángulo rectángulo: 12 cm β 9 cm Matemáticas Grado Décimo EJERCICIO 5 Si se sabe que sec θ = 6 , calcular las demás funciones 2 trigonométricas para el ángulo θ Matemáticas Grado Décimo