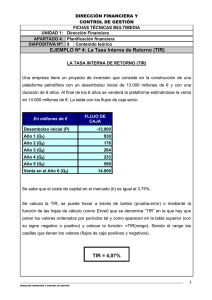
PRIMERO. Pedro se ha comprado un apartamento por 125.000 euros y espera venderlo dentro de un año por 137.000 euros. 1. ¿Cuál sería la TIR de esta inversión? 2. Si el coste del capital o tipo de interés de mercado es del 5%. ¿debería llevar a cabo esta inversión desde el punto de vista del criterio del VAN?. Razone su respuesta. SOLUCION 1. Aplicamos la fórmula de la TIR: − 𝐷0 + 𝑄1 𝑄2 + =0 (1 + 𝑟) (1 + 𝑟)2 −125.000 + 137.000 =0 (1 + 𝑟) −125.000 − 125.000𝑟 + 137.000 = 0 −125.000 + 137.000 = 125.000𝑟 𝑟= 12.000 = 0,096−→ 9,6% 125.000 2. Aplicamos la fórmula del VAN: 𝑉𝐴𝑁 = − 𝐷0 + 𝑄1 𝑄2 𝑄3 𝑄𝑛 + + + ⋯+ (1 + 𝑘) (1 + 𝑘)2 (1 + 𝑘)3 (1 + 𝑘)𝑛 Donde K= coste de capital que es un 5%, Q1 es el flujo neto de caja. Y D es el desembolso inicial que son los 125.000 euros. 𝑉𝐴𝑁 = −125.000 + 137.000 = 5476,19 𝑒𝑢𝑟𝑜𝑠 (1 + 0,05) El VAN es positivo por lo que si deberá realizar la inversión. SEGUNDO. Tienes dos alternativas de inversión: el proyecto A supone un desembolso de 1000 euros con un coste del capital del 4% y unos flujos de caja de 2000 euros el primer año y 5000 euros el segundo año. El proyecto B supone un desembolso de 10000 euros con un coste del capital del 7% y unos flujos de caja de 20000 euros el primer año y 50000 euros el segundo año. 1. Selecciona según el criterio de la TIR, VAN y payback qué proyecto elegirías. 2. ¿A partir de qué coste del capital no aceptarías ninguno de los dos proyectos porque no resultarían rentables? SOLUCION: En el proyecto A si representamos gráficamente: -1000 0 2000 5000 1 2 La fórmula para hallar el VAN: 𝑉𝐴𝑁 = − 𝐷0 + 𝑉𝐴𝑁 = −1.000 + 𝑄1 𝑄2 + (1 + 𝑘) (1 + 𝑘)2 2000 5.000 + = 5.545,86 𝑒𝑢𝑟𝑜𝑠 (1 + 0.04) (1 + 0.04)2 Por tanto, es un proyecto realizable puesto que incrementa el valor de la empresa. En el caso de la TIR: − 𝐷0 + −1.000 + 𝑄1 𝑄2 + =0 (1 + 𝑟) (1 + 𝑟)2 2.000 5.000 + + =0 (1 + 𝑟) (1 + 𝑟)2 Para solucionar esta ecuación deberemos transformarla en una ecuación de segundo grado mediante una conversión: (1 + r) = t −1.000 + 2.000 5.000 + =0 𝑡 𝑡2 Donde −1.000 𝑡 2 + 2.000 𝑡 + 5.000 = 0. Resolviendo la ecuación de segundo grado: t= −2.000 ± √2.0002 − 4 ∗ (−1.000) ∗ 5.000 𝑑𝑜𝑛𝑑𝑒 𝑠𝑒 𝑜𝑏𝑡𝑖𝑒𝑛𝑒 𝑑𝑜𝑠 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠 𝑝𝑎𝑟𝑎 𝑡 2 ∗ (−1.000) t1= -1,44 no puede ser una rentabilidad negativa. t2=3,45 si se deshace el cambio (1 + r) = 3,45 r= 2,45; por tanto, la TIR es un 245% Según el PAYBACK.Se recupera en el primer año la inversión inicial. El payback del proyecto A son 6 meses. En el proyecto B si representamos gráficamente: -10000 0 20000 50000 1 2 La fórmula para hallar el VAN: 𝑉𝐴𝑁 = − 𝐷0 + 𝑉𝐴𝑁 = −10.000 + 𝑄1 𝑄2 + (1 + 𝑘) (1 + 𝑘)2 20000 50.000 + = 52.363,53 𝑒𝑢𝑟𝑜𝑠 (1 + 0.07) (1 + 0.07)2 Por tanto, es un proyecto realizable puesto que incrementa el valor de la empresa. En el caso de la TIR: − 𝐷0 + 𝑄1 𝑄2 + =0 (1 + 𝑟) (1 + 𝑟)2 −10.000 + 20.000 50.000 + + =0 (1 + 𝑟) (1 + 𝑟)2 Para solucionar esta ecuación deberemos transformarla en una ecuación de segundo grado mediante una conversión: (1 + r) = t −10.000 + 20.000 50.000 + =0 𝑡 𝑡2 Donde −10.000 𝑡 2 + 20.000 𝑡 + 50.000 = 0. Resolviendo la ecuación de segundo grado: t= −20.000 ± √20.0002 − 4 ∗ (−10.000) ∗ 50.000 𝑑𝑜𝑛𝑑𝑒 𝑠𝑒 𝑜𝑏𝑡𝑖𝑒𝑛𝑒 𝑑𝑜𝑠 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠 𝑝𝑎𝑟𝑎 𝑡 2 ∗ (−10.000) t1= -2,35 no puede ser una rentabilidad negativa. t2=2,55 si se deshace el cambio (1 + r) = 2,55 r= 1,45; por tanto, la TIR es un 145% Según el PAYBACK.Se recupera en el primer año la inversión inicial. El payback del proyecto B son 6 meses. En resumen, según el VAN elegimos el proyecto B porque es mayor. Mientras que según la TIR elegiríamos el proyecto A porque su rentabilidad es superior TIRa=245% frente al TIRb=145%. Según el Payback es indiferente. SEGUNDO APARTADO. Si el coste del capital es superior al 245% no aceptaríamos ninguno de los proyectos porque es mayor el coste de financiación 246% que la rentabilidad que se obtiene en el proyecto A (245%) y el proyecto B (145%). TERCERO. Dados los siguientes proyectos de inversión: Proyecto A: -10000/10000/5000; Proyecto B: -10000/5000/13000; 1. ¿Cuál es preferible según el plazo de recuperación? 2. ¿Y si se utiliza el criterio del VAN, sabiendo que el coste del capital es del 10%? 3. ¿Y si se utiliza el criterio de la TIR? SOLUCION: PRIMERA PREGUNTA: PLAZO DE RECUPERACION. El proyecto A se recupera el primer año mientras que el proyecto B se recupera durante el segundo año: 1 año y 4,65 meses. Luego según este criterio se prefiere el proyecto A porque tiene un plazo menor. SEGUNDA PREGUNTA. VAN: En el proyecto A si representamos gráficamente: -10.000 0 10.000 1 5000 2 La fórmula para hallar el VAN: 𝑉𝐴𝑁 = − 𝐷0 + 𝑉𝐴𝑁 = −10.000 + 𝑄1 𝑄2 + (1 + 𝑘) (1 + 𝑘)2 10.000 5.000 + = 3.223,14 𝑒𝑢𝑟𝑜𝑠 (1 + 0.1) (1 + 0.1)2 Por tanto, es un proyecto realizable puesto que incrementa el valor de la empresa. En el proyecto B si representamos gráficamente: -10.000 5.000 13.000 0 1 2 La fórmula para hallar el VAN: 𝑉𝐴𝑁 = − 𝐷0 + 𝑉𝐴𝑁 = −10.000 + 𝑄1 𝑄2 + (1 + 𝑘) (1 + 𝑘)2 20000 50.000 + = 5.289,26 𝑒𝑢𝑟𝑜𝑠 (1 + 0.07) (1 + 0.07)2 Por tanto, es un proyecto realizable puesto que incrementa el valor de la empresa. La elección según el criterio del VAN, será el proyecto B puesto que su valor neto es mayor que el proyecto B. TERCERA PREGUNTA. ELECCION SEGÚN LA TIR: En el caso de la TIR proyecto A: − 𝐷0 + 𝑄1 𝑄2 + =0 (1 + 𝑟) (1 + 𝑟)2 −10.000 + 10.000 5.000 + + =0 (1 + 𝑟) (1 + 𝑟)2 Para solucionar esta ecuación deberemos transformarla en una ecuación de segundo grado mediante una conversión: (1 + r) = t −10.000 + 10.000 5.000 + =0 𝑡 𝑡2 Donde −10.000 𝑡 2 + 10.000 𝑡 + 5.000 = 0. Resolviendo la ecuación de segundo grado: t= −10.000 ± √10.0002 − 4 ∗ (−10.000) ∗ 5.000 𝑑𝑜𝑛𝑑𝑒 𝑠𝑒 𝑜𝑏𝑡𝑖𝑒𝑛𝑒 𝑑𝑜𝑠 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠 𝑝𝑎𝑟𝑎 𝑡 2 ∗ (−10.000) t1= - 0,366no puede ser una rentabilidad negativa. t2=1,366 si se deshace el cambio (1 + r) = 1,366 r= ; por tanto, la TIR es un 36,6% En el caso de la TIR del proyecto B: − 𝐷0 + 𝑄1 𝑄2 + =0 (1 + 𝑟) (1 + 𝑟)2 −10.000 + 5.000 13.000 + + =0 (1 + 𝑟) (1 + 𝑟)2 Para solucionar esta ecuación deberemos transformarla en una ecuación de segundo grado mediante una conversión: (1 + r) = t −10.000 + 5.000 13.000 + =0 𝑡 𝑡2 Donde −10.000 𝑡 2 + 5.000 𝑡 + 13.000 = 0. Resolviendo la ecuación de segundo grado: t= −5.000 ± √5.0002 − 4 ∗ (−10.000) ∗ 13.000 𝑑𝑜𝑛𝑑𝑒 𝑠𝑒 𝑜𝑏𝑡𝑖𝑒𝑛𝑒 𝑑𝑜𝑠 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠 𝑝𝑎𝑟𝑎 𝑡 2 ∗ (−13.000) t1= -0,705 no puede ser una rentabilidad negativa. t2= 1,0902 si se deshace el cambio (1 + r) = 1,0902 r= 0,0902; por tanto, la TIR es un 9,02% Según la TIR elegiremos el proyecto A puesto que tiene una mayor rentabilidad, un 36,6% frente al 9,02%. CUARTO. Quiero abrir un bar en Santander. No tengo nada ahorrado y acudo al Banco Santander para que me den un préstamo. Sin embargo, el Banco Santander me impone una obligación: el proyecto de mi bar debe ser rentable. Los datos que le facilito al Banco son las siguientes estimaciones: • • • Duración del proyecto: 16 años Coste del capital: 12% Los flujos netos de caja de cada año son: o El valor residual al finalizar el año 16 serán de 50.000 euros. Suponemos que no existen impuestos. Año 1 Año 2 Año 3 Año 4 Año 5 Año 6 Año 7 Año 8 -5000 -1000 2000 2000 5000 8000 20000 35000 Año 9 Año 10 Año 11 Año 12 Año 13 Año 14 Año 15 Año 16 30000 20000 30000 30000 40000 20000 10000 5000 ¿Cuál es la máxima cantidad que el Banco Santander te prestará para iniciar tu negocio? SOLUCION. Para saber la cantidad máxima que nos entregará el Banco es igual que decir que hallemos el desembolso inicial que tendrá que hacer el Banco para que a nosotros nos salga rentable y que podamos devolver con los flujos generados a lo largo de los 16 años el préstamo inicial (desembolso inicial). Por ello, utilizamos la fórmula del VAN (Valor actual neto) e igualamos a cero para calcular el desembolso inicial ( 𝐷0.) 𝑉𝐴𝑁 = − 𝐷0 + 𝑄1 𝑄2 𝑄3 𝑄𝑛 𝑉𝑎𝑙𝑜𝑟 𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙 + + +⋯+ + 2 3 𝑛 (1 + 𝑘) (1 + 𝑘) (1 + 𝑘) (1 + 𝑘) (1 + 𝑘)𝑛 𝑉𝐴𝑁 = 0 ==> 0 = − 𝐷0 − 5000 1000 2000 2000 5000 8000 − + + + + (1 + 0.12) (1 + 0.12)2 (1 + 0.12)3 (1 + 0.12)4 (1 + 0.12)5 (1 + 0.12)6 20000 35000 30000 20000 30000 + + + + + 7 8 9 10 (1 + 0.12) (1 + 0.12) (1 + 0.12) (1 + 0.12) (1 + 0.12)11 30000 40000 20000 10000 5000 + + + + + 12 13 14 15 (1 + 0.12) (1 + 0.12) (1 + 0.12) (1 + 0.12) (1 + 0.12)16 50000 + (1 + 0.12)16 Donde se obtiene que como máximo el Banco tendrá que prestar 76.990,43 euros. Si me prestara más cantidad, los flujos de caja que conseguiría no me permitiría devolver el préstamo. Con una cantidad menor (un desembolso inferior) sí que puedo devolver el préstamo y por tanto el Banco Santander me concedería el préstamo. QUINTO. Estoy indeciso en dónde emplear el dinero de mi herencia, unos 100.000 euros. Aconséjame donde debo invertirlo. Dudo entre: • • Inversión 1. Comprar un bar por 100.000 euros tras lo cual recibo unos flujos netos de caja de 5000 euros y 3000 euros respectivamente durante los dos años que me quedan para jubilarme y traspasar el local por 120000 euros al final del segundo año. Inversión 2. Invertir en un fondo de inversión al 10% recuperando la inversión al segundo año. SOLUCION En este ejercicio tendré que comparar la TIR de los dos proyectos. En la inversión 2 nos proporcionan su TIR que es el 10%. Por tanto, lo que tendré que hacer es hallar la TIR de la inversión 1 y comparar cuál de ellas me proporciona mayor rentabilidad. Inversión 1: − 𝐷0 + −100.000 + 𝑄1 𝑄2 + =0 (1 + 𝑟) (1 + 𝑟)2 5.000 3.000 + 120.000 + + =0 (1 + 𝑟) (1 + 𝑟)2 Para solucionar esta ecuación deberemos transformarla en una ecuación de segundo grado mediante una conversión: (1 + r) = t −100.000 + 5.000 123.000 + =0 𝑡 𝑡2 Donde −100.000 𝑡 2 + 5.000 𝑡 + 123.000 = 0. Resolviendo la ecuación de segundo grado: t= −5.000 ± √5.0002 − 4 ∗ (−100.000) ∗ 123.000 𝑑𝑜𝑛𝑑𝑒 𝑠𝑒 𝑜𝑏𝑡𝑖𝑒𝑛𝑒 𝑑𝑜𝑠 𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠 𝑝𝑎𝑟𝑎 𝑡 2 ∗ (−100.000) t1= -1.08 no puede ser una rentabilidad negativa. t2=1.134 si se deshace el cambio (1 + r) = 1.134 r= 0.134; por tanto, la TIR es un 13.4% Luego la rentabilidad del bar nos proporciona un 13,4% mientras que la inversión en un fondo de inversión es un 10%. Por tanto, elegiremos la inversión del bar porque su rentabilidad es superior.