Universidad de Pamplona
Facultad de Ciencias Básicas
Departamento de Matemáticas
Cálculo Integral.
Taller sección 4.3 El primer Teorema Fundamental del Cálculo(TFC)
EJEMPLOS
.
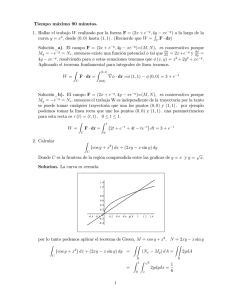
1. Dada la grá…ca:
a) Determine una fórmula y haga la grá…ca de la función de acumulación A(x) que es el área indicada.
b) ¿Cuál es la derivada de A(x) ?:
Solución.
a).
Sean f (t) la función gra…cada, A(x) área bajo la curva f (t) y (0; 1); (1; 0) dos puntos de la recta:
m=
y
y2 y 1
t2 t1
=
0 ( 1)
1 0
y1 = m(t
= 1 (Pendiente de la recta)
t1 ) = y
0 = 1(t
1)
y=t
f (t) = t
1
1 (Ecuación de la recta).
El área A(x) es igual a la integral de…nida:
Rx
A(x) = 1 (t 1)dt:
Se puede evaluar esta integral de…nida mediante un argumento geométrico; A(x) es el área de un
triángulo de modo que:
A(x) = (x
A(x) =
1)(x
(x 1)2
:
2
(x
1)=2
1)
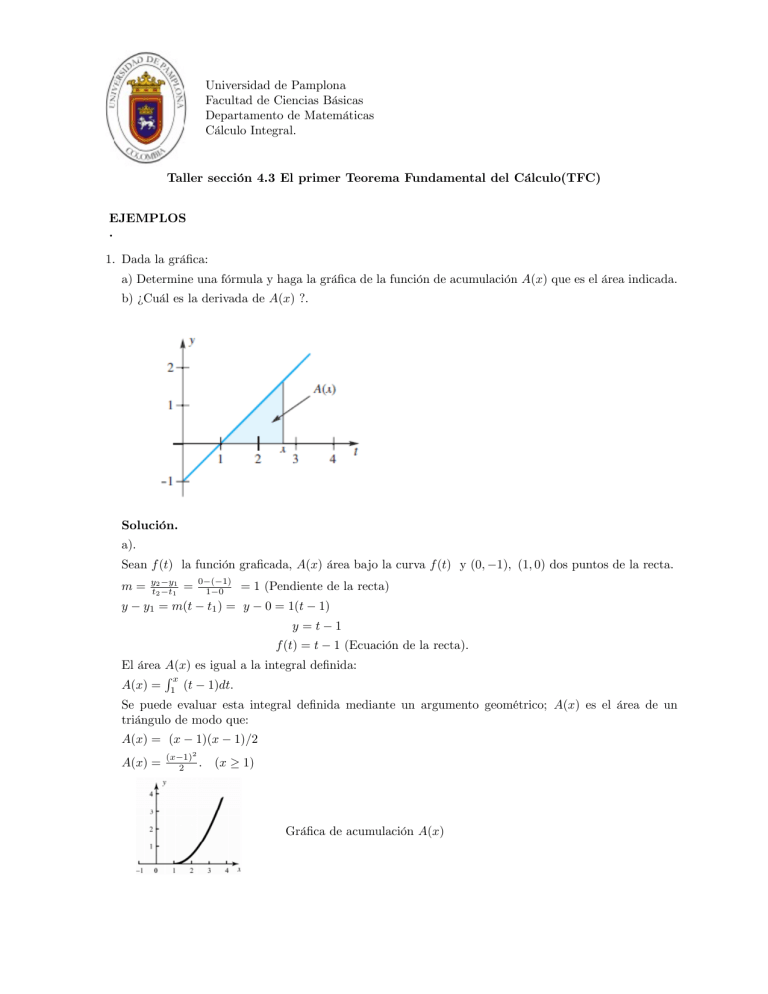
Grá…ca de acumulación A(x)
b).
A0 (x) =
2
d (x 1)
dx
2
=x 1
Rx
d
(t
En otras palabras dx
1
1)dt: = x
1:
Rx
2. Sea B(x) = 0 t2 dt el área bajo la curva y=t2 ; t = 0; t = x como se muestra en la siguiente …gura.
Determine el área de está región.
Solución.
Para determinar el área se tomará el intervalo [0; x]; una partición n subnintervalos,
t = x n 0 = nx ;el extremo derecho del i-ésimo subintervalo es ti = 0 + i t = 0 + i( nx ) = i nx , por lo
tanto la suman de Riemann es:
Pn
Pn
x x
i=1 f (ti ) t =
i=1 f (i n ) n
P
n
= nx i=1 (i nx )2
Pn
2
= nx i=1 i2 nx2
2 Pn
= nx : nx2 i=1 i2
3 Pn
= nx3 i=1 i2
Pn
Remplazando por la suma especial i=1 i2 = n(n+1)(2n+1)
se obtiene
6
x3
n3
=
n(n+1)(2n+1)
6
La integral de…nida es el limite (si esté existe) de esas sumas de Riemann
Rx
0
t2 dt: = l{m
n!1
Pn
i=1
x3
3
n!1 n
n(n+1)(2n+1)
6
x3
n!1 6
n(n+1)(2n+1)
n3
x3
l{m
6 n!1
n(n+1)(2n+1)
n3
= l{m
= l{m
=
f (ti ) t
=
x3
l{m
6 n!1
2n3 +3n2 +n
n3
=
x3
l{m
6 n!1
2+
=
x3
6
=
x3
6
3
n
+
1
n2
3
n!1 n
l{m 2 + l{m
n!1
(2)
3
= x3
2
desarrollando la parte algebraica
1
2
n!1 n
+ l{m
aplicando cada limite se obtiene
3
Entonces B(x) = x3 : Encontremos la derivada de B(x): B 0 (x) =
Rx 2
d
Por lo tanto dx
t dt = x2
0
3.
d x3
dx 3
=
3x2
3
= x2
Primer Teorema Fundamental del Cálculo (TFC)
Sea f continua en el intervalo cerrado [a; b] y sea x un punto (variable) en (a; b): Entonces
d
dx
Rx
a
f (t)dt = f (x)
Bosquejo de la demostración del Teorema.
Sea x en [a; b] ; se de…ne F (x) =
Rx
a
f (t)dt; F (x + h) =
Entonces para x en (a; b) se tiene:
Rx
d
0
dx a f (t)dt = F (x)
R x+h
a
f (t)dt:
(1)
= l{m F (x+h)h F (x)
(De…nición de derivada)
h!0
hR
i
Rx
x+h
f (t)dt:
f
(t)dt
(Usando (1))
= l{m h1 a
a
h!0
hR
i
Ra
x+h
= l{m h1 a
f (t)dt: ( ) x f (t)dt (De…nición sección 4:2)
h!0
hR
i
R x+h
a
= l{m h1 x f (t)dt: + a
f (t)dt
h!0
R x+h
= l{m h1 x f (t)dt: (Propiedad aditiva para intervalos. Teorema 4:2B)
h!0
El área bajo la curva y = f (t) de…nida en el intervalo [x; x + h] es aproximadamente igual al área del
rectángulo con ancho h y altura f (x) (veáse la …gura). Esto es,
R x+h
f (t)dt hf (x): Por lo tanto,
x
Ra
d
l{m h1 [hf (x)] = f (x)
dx x f (t)dt
h!0
4. Calcule las derivadas siguientes:
Rx 1
R x2 p
d
d
a) dx
dt
b) dx
cos tdt
1 t3 +1
3
c)
d
dx
Rx
t2
dt
x2 1+t3
solución
a).
Sea f (t) =
1
t3 +1
por primer teorema fundamental, se tiene
b) .
3
d
dx
Rx
1
dt
1 t3 +1
=
1
x3 +1
Sea u = x2 en la regla de la cadena se obtiene
R x2 p
Rup
d
d
cos tdt = du
cos tdt: du
dx 3
dx
3
p
con f (t) = cos t y du
=
2x
por
primer
teorema
fundamental,
se tiene
dx
2 p
R
p
x
d
cos tdt = cos u(2x)
dx 3
p
= 2x cos u
p
= 2x cos x2
p
R x2 p
d
por lo tanto dx
cos
tdt
=
2x
cos x2
3
c).
d
dx
Rx
t2
dt
x2 1+t3
Sea u =
con f (t) =
=
d
dx
R0
d
dx
=
t2
dt
x2 1+t3
R
x2
0
d
dx
+
t2
1+t3
+
Rx
t2
dt
0 1+t3
d
dx
Rx
t2
dt
0 1+t3
x2 en la regla de la cadena se obtiene
R u t2
R x t2
d
du
d
du 0 1+t3 dt: dx + dx 0 1+t3 dt
t2
1+t3
du
dx
y
=
2x por Primer Teorema Fundamental, se tiene
=
5. Sea A(x) =
Rx
1
u2
1 u3
+
x2
1+x3
t3 dt
a) si y = A(x); encuentre
dy
dx
= x3 :
b) Encuentre la solución de la ecuación diferencial
R4
c) Encuentre 1 t3 dt:
dy
dx
= x3 que satisface y = 0 cuando x = 1:
Solución
a).
Aplicando el primer Teorema Fundamental del cálculo,
dy
dx
= A(x) = x3
b).
Como la ecuación diferencial
dy
dx
3
= x3 es separable, se puede escribir
dy = x dx
Al integrar ambos lados se obtiene
R
y = x3 dx =
cuando x = 1 entonces se tiene que:
y = A(1) =
Se halla C; de modo que:
0=
Por lo tanto c =
1
4 :Así
14
4
R1
1
t3 dt = 0: (De…nición sección 4.2)
+C
x4
4
1
4:
c).
x4
4
+C
que la solución de la ecuación diferenfcial es:
y=
Como y = A(x) =
x4
4
1
4;
se tiene que
R4
1
t3 dt = A(4) =
4
44
4
1
4
=
255
4 :
TEOREMA: Linealidad de la Integral De…nida
Suponga que f y g son integrables en [a; b] y k una constante. Entonces kf y f + g son integrales y:
1.
2.
3.
Ra
b
Ra
b
Ra
b
kf (x)dx = k
Ra
b
f (x)dx
[f (x) + g(x)] dx =
[f (x)
g(x)] dx =
Ra
f (x)dx +
b
Ra
b
Ra
f (x)dx
b
Ra
b
g(x)dx
g(x)dx
EJEMPLO: Un objeto en el origen, en el instante t = 0, tiene velocidad, medida en metros por
segundo,
8
si 0 t 40
< t=20
2
si 40 < t 60
v(t) =
:
5 t=20
si t > 60
¿Cuándo, si sucede, el objeto regresa al origen?
solución
Ra
Sea F (a) = 0 v(t)dt posición a la posición del objeto en el instante a. La acumulación se ilustra en
la siguente …gura
Si el objeto regresa al origen en algún tiempo a, entonces a debe satisfacer F (a) = 0. El valor que se
requiere de a seguramente es mayor que 100, ya que el área debajo de la curva entre 0 y 100 debe ser
exactamente igual al área por arriba de la curva y por debajo del eje t, entre 100 y a. Por lo tanto:
R 100
Ra
Ra
F (a) = 0 v(t)dt = 0 v(t)dt + 100 v(t)dt
R 40
R 60
R 100
Ra
= 0 v(t)dt + 40 v(t)dt + 60 v(t)dt + 100 v(t)dt
Ra
+ (20)(2) + (40)(2)
+ 100 (5 t=20)dt
= (40)(2)
2
2
= 120 +
=120+
(a 100)(5
2
1
2
a2
20
5a
= 120 +
1
2
5a
= 120 +
1
2
10a
= 120 + 5a
=
1 2
40 a
a
20
2
a
40
+ 5a
)
500 +
a2
20
a2
20
100a
20
500 + 5a
500
250
130
Entonces
debemos hacer F (a) = 0. Las dos soluciones para esta ecuación cuadrática son: a = 100
p
40 30: Tomando el signo de menos da un valor
p menor que 100, que no puede ser la solución, por lo
que se descarta. La otra solución es 100 + 40 3
5
Comprobar esta solución:
R 100+40p3
F (a) = 0
v(t)dt
R 100
R 100+40p3
= 0 v(t)dt + 100
v(t)dt
=120 +
p
(100+40 3 100) 5
p
100+40 3
20
2
=0
p
Por lo tanto, el objeto regresa al origen en el instante t = 100 + 40 3 segundos.
6
EJERCICIOS
1. Dada la grá…ca:
a) Determine una fórmula y haga la grá…ca de la función de acumulación A(x) que es el área indicada.
b)¿ Cuál es la derivada de A(x) ?:
2. sea F (x) =
Rx
0
(t4 + 1)dt:
a) Encuentre F(0)
b) Sea y = F (x): Aplique el primer Teorema Fundamental del Cálculo para obtener
dy
dx
= F 0 (x) = x4 +1:
c) Encuentre la solución de está ecuación diferencial que satisface y = F (0);cuando x = 0
R1
d) Demuestre que 0 (x4 + 1)dx = 56
Rx
3. Dada la función A(x) = 0 (5 + t2 )dt , basándose del Ejemplo 2 Determinar A0 (x):
4. Calcule las derivadas siguientes:
p
Rx
d
2t2 + t dt
a) dx
0
R x2
d
b) dx
sent dt
1
R
senx
d
c) dx
t5 dt
cos x
Nota: Se sugiere, en los ejercicios 5 y 6 derivar ambos lados de la igualdad y aplicar TFC
R x2
5. Si xsen( x) = 0 f (t)dt donde f (t) es una función continua, halle f (4):
Rx
p
6. Encuentre una función f y un número a tales que 6 + a ft(t)
x; para toda x > 0:
2 dt = 2
R4
7. Utilice la propiedad aditiva para intervalos y la linealidad para evaluar 0 f (x)dx:Comience por dibujar
una grá…ca de f:
8
si 0 x < 1
< 1
x
si 1 x < 2
a) f (x) =
:
4 x si 2 x 4
b) f (x) = jx
2j
8. La velocidad de un objeto es:
8
5
si 0 t 100
<
6 t=100 si 100 < t 700
v(t) =
:
1
si si t > 7
a) Suponiendo que el objeto está en el origen en el instante 0, determine una fórmula para su posición
en el instante t (t 0)
b) ¿Cuál es la distancia más a la derecha del origen que alcanza este objeto?
c)¿Cuándo, si esto sucede, el objeto regresará al origen?.
8
0
si x < 0
>
>
<
Rx
x
si 0 x 1
9. Sea:f (x) =
y g(x) = 0 f (t)dt
2
x
si
1
<
x
2
>
>
:
0
si x > 2
a) Encuentre una expresión para g(x) similar a la correspondiente a f (x):
b)Trace las gráfcas de f y g
2