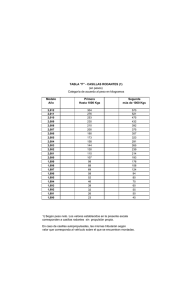
Análisis de Inversiones Método del Valor Presente Neto (VPN) El Valor Presente Neto (VPN) o Valor Actual Neto (VAN) es el método más conocido para evaluar proyectos de inversión a largo plazo, ya que permite determinar si una inversión cumple con el objetivo básico financiero: Maximizar la inversión. Es un procedimiento que permite calcular el valor presente de un determinado número de flujos de caja futuros, originados por una inversión. UAEM FCQeI Ing. Rafael Velázquez Casillas Básicamente consiste en actualizar (encontrar su valor equivalente en el presente) los cobros y pagos futuros de un proyecto o inversión y restarle la Inversión inicial para conocer cuanto se va a ganar o perder con la misma. La forma más general de expresarlo es la siguiente: 𝑉𝑃𝑁 = −𝑃 + 𝐹𝑁𝐸 (1 + 𝑖)𝑛 Que se desglosa así 𝑉𝑃𝑁 = −𝑃 + 𝐹𝑁𝐸1 𝐹𝑁𝐸2 𝐹𝑁𝐸3 𝐹𝑁𝐸𝑛 + + + ⋯ + 1+𝑖 1 1+𝑖 2 1+𝑖 3 1+𝑖 𝑛 Ya te habrás dado cuenta que lo que se está haciendo es usar la Fórmula Básica para traer al presente los flujos futuros y restar la inversión Donde P = Inversión Inicial FNE = Flujo Neto de Efectivo (ganancia futura prometida por el proyecto, meno gastos e impuestos) i = Tasa de descuento (que en este caso es la TREMA) n = Periodos del proyecto UAEM FCQeI Ing. Rafael Velázquez Casillas Criterio de decisión El método de Valor Presente Neto lo que busca es ayudar a tomar la decisión de invertir o no invertir en cierto proyecto (ahorro bancario, negocio, proyecto productivo, inversión financiera, etc.) con el afán de obtener ganancias. Cómo se ve en el concepto del método, lo que hace es comparar las ganancias futuras prometidas contra la inversión requerida (y ya sabemos que para poder compararlas deben estar en el mismo punto del tiempo, en este caso el Presente). De esta forma: Si VPN > 0 se acepta la inversión Si VPN < 0 se rechaza la inversión UAEM FCQeI Ing. Rafael Velázquez Casillas Hagamos un ejercicio par entender el método: Se tiene un proyecto de inversión que requiere una inversión inicial de 1,000 USD y a cambio ofrece ganancias de 260 el primer año, 310 el segundo, 330 el tercero, 400 el cuarto año y 505 el quinto. Si el posible inversionista ha definido su TREMA en 10% ¿Debe aceptar invertir en el proyecto? 505 400 310 Aplicamos el método 330 𝑉𝑃𝑁 = −𝑃 + 260 0 1 2 3 4 𝐹𝑁𝐸1 𝐹𝑁𝐸2 𝐹𝑁𝐸3 𝐹𝑁𝐸𝑛 + + + ⋯ + 1+𝑖 1 1+𝑖 2 1+𝑖 3 1+𝑖 𝑛 5 𝑉𝑃𝑁 = −1,000 + 260 1 + 0.1 + 1 310 1 + 0.1 + 2 330 1 + 0.1 + 3 400 1 + 0.1 + 4 505 1 + 0.1 5 = 327.26 > 0 1000 ¿Pero qué pasaría si este proyecto se le presentara a otro inversionista cuya TREMA es de 25%? 𝑉𝑃𝑁 = −1,000 + 260 1 + 0.25 + 1 310 1 + 0.25 + 2 330 1 + 0.25 + 3 400 1 + 0.25 + 4 505 1 + 0.25 5 = -95.32 < 0 ¿Quiere decir esto que el segundo inversionista perdería dinero? No. Ganaría lo mismo que el primero; el proyecto ofrece las mismas ganancias a cualquiera que invierta. El resultado negativo significa que el proyecto no pagaría la TREMA que pide el inversionista. UAEM FCQeI Ing. Rafael Velázquez Casillas Existen dos alternativas de inversión, ambas de 15,000 USD. La primera ofrece un pagar ganancias de 5,500 al final de cada uno de los próximos cuatro años. La segunda ofrece un pago inicial de 4,000 el primer año y un aumento de 1,200 en c/u de los siguientes tres años. Si la TREMA del inversionista es de 15%, decida cual alternativa es mejor. Proyecto A Podemos ordenar los datos en una tabla como la siguiente: Año 0 A Vemos que se trata de una Serie Uniforme por lo que podemos representar el VPN de la siguiente manera: 1+𝑖 𝑛−1 𝑉𝑃𝑁 = −𝑃 + 𝐴 𝑖 1+𝑖 𝑛 B 1.15 4 − 1 𝑉𝑃𝑁 = −15,000 + 5,500 = 702.38 0.15 1.15 4 - 15,000 - 15,000 1 5,500 4,000 2 5,500 5,200 3 5,500 6,400 4 5,500 7,600 Proyecto B Serie Uniforme del G 𝑉𝑃𝑁 = −15,000 + 4,000 (1.15)4 −1 0.15 (1.15)4 11,419.91 Conclusión: Gradiente 1,200 (1.15)4 −1 1 −4 + 0.15 0.15 (1.15)4 = 963.64 4,543.72 • Ambos proyectos son buenas alternativas de inversión (tienen VPN positivo) • El proyecto B es mejor que el A porque tiene un VPN mayor (le va a pagar una tasa más alta) UAEM FCQeI Ing. Rafael Velázquez Casillas Ahora, la tarea: UAEM FCQeI Ing. Rafael Velázquez Casillas