08-Integrales

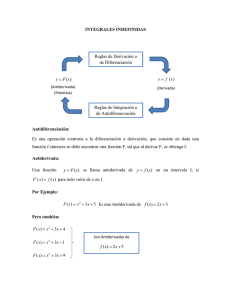
INTEGRAL DE UNA FUNCIÓN
Por:
Ing. Mario René De León García.
1.
ANTIDERIVADA DE UNA FUNCIÓN
En las unidades anteriores se estudió el concepto de la derivada de una función, así como sus aplicaciones, ahora se
introducirá al estudiante a temas de Cálculo Diferencial, suponga la siguiente función:
Cuya grafica es la siguiente:
y
x
Para obtener la primera derivada de la función
, se aplica el operador
a ambos lados de la igualdad:
Aplicando las reglas correspondientes, se obtiene la derivada de la función:
La derivada de una función es otra función a la que se le llamara
Para derivar los términos de la función
en este caso:
se aplicó entre otras, la siguiente fórmula de derivación:
2
Integral de una función
La regla para derivar
indica que el exponente pasa a multiplicar, mientras que el exponente en la variable se reduce
en uno.
La mayor parte de funciones matemáticas tiene una función inversa, por ejemplo: la función exponencial y el logaritmo;
coseno y el coseno inverso; raíz cuadrada y potencia cuadrada; tangente inversa y tangente, entre otras. Dos funciones que son
inversas entre sí deben cumplir con:
Esta propiedad indica que la función inversa cancela la acción de la función, regresando al valor inicial, por ejemplo:
. A continuación se estudia el proceso inverso que permite anular las acciones de la derivación para regresar a la función
inicial. La operación que anula las acciones de derivación, se llama “antiderivación” o “integración indefinida”, cuya notación es la
siguiente:
Regresando al ejemplo inicial, se establecerá el procedimiento para encontrar la función de Antiderivada de
debería ser
. Según lo discutido previamente, se debe cumplir que:
Recuerde la función
que es el resultado de la derivada de
, la cual
:
O bien:
Para antiderivar
realizamos las acciones contrarias a la de derivación, esto sería: aumentar el exponente en uno y
dividir el término sobre este valor, es decir:
. Si se deriva
se obtiene nuevamente
, lo que demuestra que el proceso
de antiderivación explicado es correcto. Siguiendo estas ideas se podría encontrar la Antiderivada de
al lado derecho de la ecuación de derivada anterior:
, iniciando por trasladar
Aplicando el operador de integración:
Se obtiene que:
Observe que al final de la función de Antiderivada debe haber un número, ya que la derivada de una constante es cero,
por lo que en el proceso de antiderivación o integración se debe considerar que al final hay un cero y su Antiderivada es un valor
contante, ¿pero qué valor? Pues no se conoce y solo se sabe que debe ser un valor constante, por esta razón, la Antiderivada más
general de
es:
Donde
es un valor constante que pertenece a los números reales
Preparado por: Ing. Mario René De León García
3
Integral de una función
Como
es un valor que pertenece a los reales, la Antiderivada no es una función única, es una “familia de funciones”,
una diferente para cada valor de , las cuales pueden representarse por una “familia de graficas”. Todas las graficas tienen la
misma forma pero trasladadas verticalmente, debido a los valores de
que distinguen a cada Antiderivada particular.
y
x
Para obtener una Antiderivada particular, se debe conocer al menos un par ordenado de la función que se quiere
encontrar. Para la función
dada inicialmente, se puede utilizar el punto
que permitirá encontrar el valor
que
particulariza la Antiderivada:
Se obtiene:
Por lo tanto, la Antiderivada particular cuya grafica pasa por el punto
está dada por:
En este caso se conocía la ecuación de la función estudiada en el ejemplo, así como su grafica. En general cuando se
busca la Antiderivada de una función no se conoce su grafica o ecuación, por lo que se obtendrá una función o Antiderivada
general. Las siguientes definiciones son útiles en el estudio del Cálculo integral:
ANTIDERIVADA O PRIMITIVA DE UNA FUNCIÓN
1.
Definición de Antiderivada o primitiva:
, siempre que se cumpla que
es una Antiderivada o Primitiva de
para todo valor de
en el intervalo
en un intervalo
.
2.
Forma de la Antiderivada o primitiva: Si
, entonces la Antiderivada mas general de
es una Antiderivada o Primitiva de
sobre
viene dada por:
en un intervalo
Siempre que
La expresión anterior se lee como “Antiderivada o primitiva de
con respecto a
”, donde el
diferencial
sirve para idetificar a
como la variable de integración. Antiderivada e integral indefinida
se utilizan como sinónimos.
Preparado por: Ing. Mario René De León García
Integral de una función
4
Al igual que en la derivada, es necesario conocer reglas o fórmulas que permitan el proceso de integración para obtener la
función de Antiderivada. A continuación se presentan aquellas que son las más usuales:
REGLAS GENERALES
1)
3)
2)
4)
REGLAS DE INTEGRACIÓN DE FUNCIONES ALGEBRAICAS
5)
7)
6)
FUNCIONES TRIGONOMÉTRICAS
14)
8)
9)
15)
10)
16)
11)
17)
12)
13)
LOGARÍTMICAS Y EXPONENCIALES
14)
16)
15)
FUNCIONES TRIGONOMÉTRICAS INVERSAS
19)
17)
18)
2.
ECUACIONES DIFERENCIALES
Dada la siguiente ecuación:
A este tipo de ecuaciones se les llama “ecuaciones diferenciales” (de primer orden) y se dice que la misma tiene una
solución particular
o “solución singular” cuando se conoce un punto o condición de la solución. Observe que no es más
que encontrar la Antiderivada de
cuya grafica pasa por un punto particular
.
Preparado por: Ing. Mario René De León García
5
Integral de una función
Las ecuaciones diferenciales son de mucha utilidad en problemas de aplicación, principalmente en fenómenos físicos,
como por ejemplo en descomposición radioactiva, electromagnetismo, crecimiento poblacional y otros.
valor de
Por otra parte, la primera derivada de una función permite calcular la pendiente de la recta tangente a una curva para un
, por esta razón la expresión:
Representa los valores de la pendiente de las rectas tangentes a la función
, si esta es una solución particular o singular de la
ecuación diferencial. Si no existen condiciones o al menos un punto conocido de
, la solución de la ecuación es general y la
misma representa el conjunto de todas las pendientes de todas las soluciones posibles de la ecuación. Este caso puede ser
representado por lo que se denomina un “campo de pendientes”.
Para el ejercicio que se viene estudiando:
O simplemente:
Al representar esta ecuación mediante un campo de pendientes se obtiene:
y 10
y
5
-2.0 -1.8 -1.6 -1.4 -1.2 -1.0 -0.8 -0.6 -0.4 -0.2
0.2 0.4 0.6 0.8 1.0
x
x
-5
-10
El campo de pendientes permite visualizar en forma aproximada, la forma de la grafica de
que es solución de la
ecuación, tomando como referencia un punto y siguiendo la trayectoria marcada por las pendientes. Esta grafica consiste en
pequeños segmentos de recta que se dibujan en puntos
del plano cartesiano y que representan las rectas tangentes a la
curva
con pendiente
. Si en lugar de segmentos de recta se utilizan vectores, la grafica se denomina “campo de vectores”,
tal como se muestra en la grafica anterior y que se compara con algunas soluciones particulares de la ecuación.
Para dibujar un campo de vectores con Scientific Notebook, la ecuación diferencial de la forma
forma vectorial:
Luego se sigue la siguiente ruta:
Compute + Plot 2D + Vector Field
Preparado por: Ing. Mario René De León García
, se escribe de
6
Integral de una función
EJERCICIO 1:
Obtenga las siguientes integrales indefinidas generales:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
EJERCICIO 2:
Encuentre las soluciones singulares (generales) de las siguientes ecuaciones diferenciales, tomando en
cuenta la o las condiciones dadas.
1.
; si la solución pasa por el punto
2.
3.
4.
; si
y
; si
; si
.
y
.
Preparado por: Ing. Mario René De León García
7
Integral de una función
ÁREA BAJO LA CURVA Y LA INTEGRAL DEFINIDA
1.
APROXIMANDO EL ÁREA BAJO LA CURVA
Dada la función siguiente:
La grafica de esta función en el intervalo
es:
y 30
20
10
0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
x
Una de las aplicaciones del Cálculo Integral es calcular el área de la región formada por la curva de una función y el eje de
las abscisas, que equivale a decir “el área bajo la curva”. Para entender el tema, se calculará de forma aproximada el área bajo de
la curva de la función dada, para esto se dividirá la región en 8 rectángulos de ancho constante y cuya altura coincida con el punto
medio del ancho del rectángulo. Observe esto en la siguiente grafica:
y 30
20
10
0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
Preparado por: Ing. Mario René De León García
x
8
Integral de una función
En la figura se ilustra el quinto rectángulo cuya altura es igual al valor de la función valuada en el punto medio del ancho
del rectángulo. En este caso particular el valor del punto medio es
, la altura del rectángulo
y su
ancho
. El área del rectángulo es solo una parte del área bajo la curva, por lo que se denotara como
cuyo valor para
el quinto rectángulo se calcula de la forma siguiente:
Para estimar el área bajo la curva en el intervalo
se debe determinar el área de los ocho rectángulos y sumarlas.
El valor obtenido de esta forma es una aproximación del valor del área real, ya que no se tiene seguridad de que las pequeñas
regiones fuera de la curva compensen las regiones no tomadas en cuenta dentro de la misma.
La siguiente tabla, elaborada en una hoja electrónica, muestra el cálculo de las áreas de los ocho rectángulos, así como el
valor aproximado del área bajo la curva:
1
2
3
4
5
6
7
8
0.25
0.75
1.25
1.75
2.25
2.75
3.25
3.75
0.05859375
1.37109375
5.37109375
12.05859375
19.93359375
25.99609375
25.74609375
13.18359375
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.029296875
0.685546875
2.685546875
6.029296875
9.966796875
12.99804688
12.87304688
6.591796875
51.859375000
Ahora se buscará mecanizar este procedimiento para cualquier curva sobre el eje de las abscisas y que sea continua en
un intervalo
. Si se considera que el ancho
de todos los rectángulos son iguales, su valor es igual a:
Donde
El valor del punto medio
es el número de rectángulos verticales en que se divide la región.
para el i – ésimo rectángulo viene dado por:
Estas fórmulas puede comprobarlas con el ejercicio anterior.
Otra forma de calcular el área aproximada de la región es utilizando la notación de sumatoria, para lo cual se utiliza la letra
griega mayúscula Sigma “ ”. La suma de las áreas de los ocho rectángulos se expresa de la forma siguiente:
Donde
representa el área del rectángulo , cuyo valor se hace variar de 1 a 8, según los límites de la sumatoria. Si
, el área se puede expresar de la forma siguiente.
Sustituyendo el valor de
indicado previamente se obtiene:
Preparado por: Ing. Mario René De León García
9
Integral de una función
Si
, al sustituir en la expresión anterior se tiene:
Al simplificar:
El valor
es un valor constante y se puede sacar de la sumatoria y al sustituir en la función
, se obtiene
Utilizando Scientific Notebook para resolver esta sumatoria se obtiene:
El dato obtenido coincide con el calculado previamente en la tabla.
La aproximación del área bajo la curva mejora a medida que el número de rectángulos “ ” utilizados sea mayor, pero esto
hace que al mismo tiempo el ancho de los rectángulos “ ” decrezca. Esto se ilustra en las siguientes graficas:
y 30
y 30
y 30
20
20
20
10
10
10
0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
x
Área aproximada con 20 rectángulos
0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
Área aproximada con 30 rectángulos
x
0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
x
Área aproximada con 50 rectángulos
Para obtener el valor exacto del área bajo la curva es necesario hacer que
, cuando esto sucede el ancho de los
rectángulos es muy cercano a cero,
y por lo tanto este ancho se convierte en un diferencial,
. Por lo anterior, el
área bajo la curva en forma exacta puede ser expresada de la forma siguiente:
O bien:
Preparado por: Ing. Mario René De León García
10
Integral de una función
2.
CÁLCULO DE ÁREAS MEDIANTE SUMATORIAS
Previamente se estudió la forma de calcular el área bajo la curva de la función
en el intervalo
Al usar un procedimiento de sumatorias se estableció que esta área puede calcularse al resolver la siguiente expresión.
.
El valor de la sumatoria se determinó con Scientific Notebook, pero al utilizar un procedimiento manual se requiere un
buen conocimiento de algebra y de fórmulas que permita calcular las sumatorias de una forma sencilla. A continuación se
presentan algunas.
REGLAS GENERALES
1)
3)
2)
4)
Para todo valor
Para todo valor
SUMATORIAS ESPECIALES
5)
7)
6)
Para calcular el área bajo la curva de una función con Scientific Notebook, basta con escribir la función, luego se sigue la
siguiente ruta desde la barra de menús:
Compute + Calculus + Aproximate integrate . . .
El Programa le preguntará que método de cálculo utilizará, para el ejemplo resuelto en este documento se utilizó “Punto
Medio”, esto se selecciona en la ventana “Formula”. En la opción “subintervals” se selecciona el número de rectángulos que se
desea incluir en la región; luego en la opción “Lower End of Range” se indica el límite inferior de la región, mientras que en “upper
End of Range” se indica el límite superior. Luego de presionar el botón “OK” aparecerá la sumatoria que calcula el área con el
método indicado; para obtener el valor numérico presione “Evaluate” o “Evaluate numerically”.
Preparado por: Ing. Mario René De León García
11
Integral de una función
Además del punto medio existen otros métodos de cálculo, que están basados en el tipo de rectángulos que se colocarán
dentro de la región a calcular, los que se muestran en las siguientes ilustraciones:
y 30
y 30
20
20
10
10
0
0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
x
1.5
2.0
2.5
3.0
3.5
4.0
x
Rectángulos con vértice derecho sobre la curva
Rectángulos con vértice izquierdo sobre la curva
y 30
y 30
20
20
10
10
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
0
x
-10
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
3.5
4.0
x
-10
Rectángulos inscritos en la región.
El área es menor al de la región.
Rectángulos circunscritos a la región
El área es mayor al de la región
y 30
y 30
20
20
10
10
0
1.0
-10
-10
0
0.5
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
0
x
0.5
1.0
1.5
2.0
2.5
3.0
x
-10
-10
Regla del Trapecio
Calcula el área utilizando trapecios en lugar de rectángulos, que
es equivalente al promedio de los métodos del vértice izquierdo
y derecho.
Regla de Simpson
En lugar de utilizar segmentos de recta, utiliza una parábola
para aproximar el área bajo la curva. Para el cálculo se
requiere de tres puntos consecutivos dentro de cada intervalo
.
Preparado por: Ing. Mario René De León García
12
Integral de una función
Para generar estas graficas en Scientific Notebook, se sigue la siguiente ruta desde la barra de menús:
Compute + Calculus + Plot Aproximate integrate
Entre a propiedades de la grafica y edite la grafica para observar la región de interés de la forma que guste.
Se invita al lector a investigar más sobre estos métodos aproximados para el cálculo del área bajo la curva de una función
positiva en un intervalo cerrado.
Con base en lo anterior, se puede realizar la siguiente definición:
INTEGRAL DEFINIDA
Sea
una función continua y definida en el intervalo
la función y el eje de las abscisas se dividen en
. Si en este intervalo la región entre la curva de
sub intervalos de igual ancho de tamaño
rectángulos que aproximan el área de la región. Además, si
es la posición que define la altura
cada rectángulo. Entonces la integral definida de
hasta
, desde
Esto es cierto siempre que el límite exista, en este caso se dice que
, formando
de
, es:
es integrable sobre
. La
se llama “Suma de Riemann”, en honor al matemático alemán Bernhard Riemann.
expresión
Esta definición lleva a interpretar una integral definida de la forma siguiente:
y
LA INTEGRAL DEFINIDA COMO ÁREA DE UNA REGIÓN
Si una función
es continúa y positiva (su grafica está por
encima del eje de las abscisas) en un intervalo
, entonces, el
área de la región definida por la curva, el eje de las abscisas y las rectas
y
viene dada por la siguiente integral definida:
A
x
Preparado por: Ing. Mario René De León García
Integral de una función
Para simplificar los cálculos del cálculo de la integral, se pueden tomar los valores
derecho de cada uno de los rectángulos, entonces se tiene que:
13
como los valores del extremo
TEOREMA
Sea
una función continua y definida en el intervalo
, entonces:
Donde:
EJERCICIO 3:
Utilizando la definición por límite de la sumatoria de Riemman y el teorema anterior, determine el
valor de las siguientes integrales definidas:
1.
2.
3.
4.
EJERCICIO 4:
Evalúe cada una de las siguientes integrales, interpretándolas en términos de áreas.
Recomendación: grafique la función del integrando en el intervalo de integración, calcule la
integral según la figura geométrica que se forma y el signo que le corresponda,
1.
2.
3.
4.
Preparado por: Ing. Mario René De León García
14
Integral de una función
3.
PROPIEDADES DE LAS INTEGRALES DEFINIDAS
Previamente se definió la integral como el área bajo la curva, por lo que su valor depende del comportamiento de la grafica
de la función en un intervalo cerrado, de aquí algunas de las propiedades.
3.1
Si
está definida en
y
, entonces:
Razón: esta integral define una línea recta vertical que como consecuencia no
tiene área, solo longitud.
3.2
Si
es integrable en el intervalo
x
, entonces se cumple que:
La integral esta deducida para calcular el área bajo la curva de izquierda a derecha, de tal forma que los diferenciales
son positivos en ese sentido, si se invierten los límites de integración, los diferenciales se vuelven negativos. Como el área es una
magnitud positiva, se le debe anteponer un signo negativo a la integral para que el valor de área sea el correcto.
y
3.3
Si
es integrable en el intervalo
“ ” que cumple con
, entonces:
, de tal forma que hay un valor
La integral expresa que si una región se divide en dos sub regiones a partir de
, el
área total de la región es igual a la suma de las áreas de las sub regiones. Vea la figura
adjunta que ilustra esta propiedad.
3.4
Si
es negativa (su grafica está por debajo del eje de las abscisas) e
integrable en el intervalo
, el área bajo la curva de la función
viene definida por la siguiente integral.
x
y
x
A
Siendo
positivo, al estar la grafica por debajo del eje de las abscisas los
valores de
son negativos, en este caso se le antepone a la integral un signo
negativo para obtener el valor correcto de área.
Preparado por: Ing. Mario René De León García
15
Integral de una función
3.5
y
Si
es negativa en el intervalo
y positiva en el intervalo
, entonces el área bajo la curva de la función en el intervalo
viene dada por:
Razón: El área total de la región es igual a la suma de las áreas de las
subregiones que la forman, anteponiéndole a cada integral el signo que le corresponde.
4.
x
TEOREMA FUNDAMENTAL DEL CÁLCULO
Previamente se menciono la relación inversa que tienen la derivación y la integración, la cual fue estudiada en su tiempo
por Isaac Newton y Gottfried Leibniz, con trabajos separados pero con las mismas ideas. La relación entre el Cálculo diferencial y
el Cálculo integral viene enunciada a través del teorema denominado “Teorema fundamental del Cálculo”, entre otras cosas, el
teorema establece la forma de calcular áreas e integrales de una forma equivalente al del límite de una sumatoria.
TEOREMA FUNDAMENTAL DEL CÁLCULO
Sea
1.
una función continua e integrable en el intervalo
, entonces:
La integral de una función positiva
es otra función
, la cual puede ser interpretada como el área
bajo la curva de
desde un valor fijo
hasta el valor que se le quiera dar a esta variable,
siempre y cuando la función siga siendo positiva e integrable. Esto se expresa a través de:
para
En este caso se cumple que
2.
Si
es una Antiderivada de
, o bien:
, de tal forma que
, entonces:
EJERCICIO 5:
Use la parte 1 del teorema fundamental del cálculo para encontrar la derivada de cada una de las
siguientes funciones:
1.
2.
3.
4.
Preparado por: Ing. Mario René De León García
16
Integral de una función
EJERCICIO 6:
Evalúe cada una de las siguientes integrales
1.
2.
3.
4.
REGLA DE LA CADENA PARA LA INTEGRAL
1.
ANTIDERIVADA DE UNA FUNCIÓN COMPUESTA
Sea
continua y diferenciable en el intervalo
Si
en una función compuesta de la forma
entonces:
Función Externa
y si
, además,
una función continúa en el mismo intervalo.
es una antiderivada o primitiva de
en
,
Derivada de la función interna
Función Interna
Esta operación resulta ser la inversa de la regla de la cadena en la derivación.
Ejemplo:
Dada la función.
La derivada de esta función es:
En esta ecuación
es la derivada de la potencia cubica, mientras que
Al realizar el proceso inverso se tiene:
En el proceso inverso, la función compuesta es
de la forma
, mientras que la función interna es
es:
es la derivada de la función interior.
, siendo la función externa una potencia cuadrada
y su derivada es
. Si una antiderivada de
Preparado por: Ing. Mario René De León García
Integral de una función
17
Entonces, por definición:
Siendo
2.
una antiderivada de la función
.
CAMBIO DE VARIABLES PARA CÁLCULO DE INTEGRALES
Para una integral de la forma:
Puede resolverse de forma sencilla utilizando un cambio de variable, donde:
Al derivar se obtiene:
Donde:
Al sustituir se obtiene:
Siempre y cuando
. Resumiendo lo anterior se tiene:
Este procedimiento es útil para encontrar la antiderivada de una función compuesta acompañada de la derivada de la
función interna.
En la tabla que aparece en la siguiente página, se han arreglado las antiderivadas de las funciones más usuales para el
uso de la regla de la cadena para antiderivadas.
Preparado por: Ing. Mario René De León García
18
Integral de una función
REGLAS BÁSICAS DE INTEGRACIÓN
Sea
constante
1)
2)
5)
una función de , de la forma
. Sean las constantes
un número real positivo diferente de cero.
4)
FUNCIONES TRIGONOMÉTRICAS
11)
12)
7)
13)
8)
14)
9)
10)
LOGARÍTMICAS Y EXPONENCIALES
16)
15)
17)
números reales y la
REGLAS DE INTEGRACIÓN DE FUNCIONES ALGEBRAICAS
3)
6)
14)
y
FUNCIONES TRIGONOMÉTRICAS INVERSAS
19)
18)
Preparado por: Ing. Mario René De León García
Integral de una función
EJERCICIO 7:
Evalúe cada una de las siguientes integrales indefinidas
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Preparado por: Ing. Mario René De León García
19