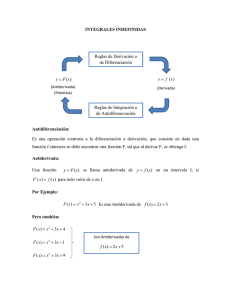
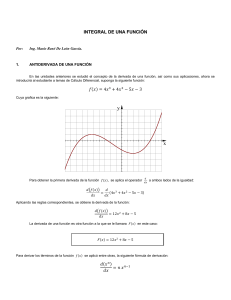
Función Derivada función Antiderivada F(x)= 𝑥 4 F´(x)= 4𝑥 3 F(x)= 4𝑥 3 F(x)= 𝑥 4 F(x)= ln x F´(x)= F(x)= sen x F´(x)= cos x 1 𝑥 F(x)= 1 𝑥 F(x)= cos x F(x)= ln x F(x)= sen x Ejercicio: calcular la antiderivada de f(x)= 3x² Solución: la función es f(x)= x³ porque f´(x)= 3x² Nota: Para una función dada la antiderivada no es única, en el ejercicio anterior se puede observar que para f(x)= 3x² también son antiderivadas las siguientes funciones Puesto que al derivar cualquiera de estas se obtiene 3x² x³ + 1 x³ + 3 x³ + 12 etc. La antiderivada más general de f(x)= 3x² es x³ + c donde c es una constante cualquiera llamada constante de integración. Ejercicio: calcular la antiderivada más general de f(x)= 𝑥 5 Solución: la función es f(x)= 𝑥6 6 +c NOTACIÓN: La antiderivada recibe también el nombre de integral indefinida y para indicarla se usa la notación: 𝒇 𝒙 𝒅 𝒙 donde: 𝑠𝑒 𝑙𝑙𝑎𝑚𝑎 𝑠𝑖𝑚𝑏𝑜𝑙𝑜 𝑑𝑒 𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑐𝑖ó𝑛 𝑦 𝑓 𝑥 𝑠𝑒 𝑙𝑙𝑎𝑚𝑎 𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑛𝑑𝑜 𝑓 𝑥 𝑑 𝑥 recibe el nombre de integral indefinida de f(x) respecto a x, dx indica que la variable de integración es x Ejemplo: calcular solución: 4𝑥 3 𝑑𝑥 4𝑥 3 𝑑𝑥 = 𝑥 4 + 𝑐 Ejemplo: calcular cos 𝑥 𝑑𝑥 solución: cos 𝑥 𝑑𝑥 = sen x + 𝑐 Ejemplo: calcular 1/𝑥 𝑑𝑥 1 𝑑𝑥 𝑥 = ln x+𝑐 solución: TÉCNICAS DE INTEGRACIÒN Método de sustitución (cambio de variable) Consiste en igualar una parte del integrando a una nueva variables. Por ejemplo u llamada variable auxiliar. Luego de esto, se debe calcular la derivada de la variable auxiliar y realizar las operaciones necesarias, para que ni en el integrando ni en el diferencial, aparezca alguna expresión en términos de la variable original. A esto se le denomina cambio de variable (sustitución). Luego de hacer efectiva la sustitución por lo general se obtienen integrales más sencillas que la original, las cuales se resuelven aplicando lo aprendido por medio de las reglas básicas. Es importante señalar que el resultado de la integración debe estar en función de la variable original por lo que se acostumbra a emplear el término “devolviendo el cambio de variable” para reseñar el proceso mediante el cual la variable auxiliar desaparece de la respuesta definitiva. 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑟: 12𝑥 2 4𝑥 3 + 2 5 𝑑𝑥 U= 4x³ + 2 du= 12x² dx = 12𝑥 2 4𝑥 3 + 2 5 𝑑𝑥 𝑢5 𝑑𝑢 = 𝑢6 6 +c = 6 3 4𝑥 +2 6 +c Calcular 2𝑥𝑑𝑥 𝑥2 + 5 U= 𝑥 2 + 5 du= 2xdx 4 = 𝑑𝑢 𝑢 4 = 𝑢 −4 𝑑𝑢 2𝑥𝑑𝑥 𝑥 2 +5 4 = 𝑢−3 −3 +c =- =- 1 3𝑢3 +𝑐 1 3 𝑥 2 +5 3 +𝑐 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑟: 4𝑥 + 1𝑑𝑥 U= 4x + 1 du= 4dx 𝑑𝑢 = dx 4 = 𝑢 𝑑𝑢 4 1 = 4 1 𝑢2 = 4𝑥 + 1𝑑𝑥 3 𝑢2 1 +𝑐 𝑑𝑢 = 3 4 2 1 6 3 2 4𝑥 + 1 + c = 1 6 3 2 𝑢 +c Calcular 𝑑𝑥 𝑥 ln 𝑥 U= ln x 1 𝑥 du= dx = 𝑑𝑢 𝑢 = 𝑢−1 𝑑𝑢 𝑑𝑥 𝑥 ln 𝑥 = ln 𝑢 + 𝑐 = ln ln 𝑥 + 𝑐 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑟 𝑥2 𝑒 1+4𝑥 3 U= 1 + 𝑥 3 du= 12𝑥 2 dx 𝑑𝑢 = 𝑥 2 𝑑𝑥 12 𝑑𝑥 = 𝑒𝑢 𝑑𝑢 12 = 1 12 2 𝑥 𝑒 𝑒𝑢 1+4𝑥 3 +𝑐 = 𝑑𝑥 1 12 3 1+𝑥 𝑒 +𝑐 • Método de integración por partes 2. RESOLUCION DE INTEGRACIÓN POR PARTES De la fórmula para la derivada del producto de dos funciones, se obtiene el método de integración por partes. Si f y g son dos funciones diferenciables, entonces: Dx [f(x) g(x)] = f(x)g´(x) + g(x)f´(x) f(x)g´(x) = Dx [f(x)g(x)] – g(x)f´(x) Ahora, si se aplican integrales a cada miembro de esta ecuación, se tiene que: 𝑓 𝑥 𝑔´ 𝑥 𝑑𝑥 = 𝐷𝑥 𝑓 𝑥 𝑔(𝑥) 𝑑𝑥 − 𝑔 𝑥 𝑓´ 𝑥 𝑑𝑥 Integrando lo que es posible integrar se obtiene: 𝑓 𝑥 𝑔´ 𝑥 𝑑𝑥 = 𝑓 𝑥 𝑔(𝑥) 𝑑𝑥 − 𝑔 𝑥 𝑓´ 𝑥 𝑑𝑥 (1) La ecuación (1) se llama fórmula para integración por partes. Frecuentemente se utiliza una expresión equivalente a (1) lo cual se obtiene al realizar los siguientes cambios de variables: U= f(x) y v = g(x) Al hacer las derivadas de u y v respectivamente se obtiene: du = f´(x)dx y dv = g´(x)dx Así que la ecuación (1) se transforma en: 𝑢𝑑𝑣 = 𝑢𝑣 − 𝑣𝑑𝑢 (Ecuación 1) Este método se utiliza cuando se desea integrar un producto de funciones diferentes 𝑢𝑑𝑣 = 𝑢𝑣 − 𝑣𝑑𝑢 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑟 𝑥𝑒 3𝑥 𝑑𝑥 u 𝑒 3𝑥 =𝑥 − 3 dv Se deriva y se integra U=x du = dx dv = 𝑒 3𝑥 v= 𝑒 3𝑥 3 𝑒 3𝑥 𝑑𝑥 3 =𝑥 𝑥𝑒 3𝑥 𝑑𝑥 𝑒 3𝑥 3 − 𝑒 3𝑥 9 +c El método de integración por partes facilito los cálculos sin embargo se debe tener mucho cuidado al momento de asignar u y dv pues una asignación equivocada puede complicar los cálculos en lugar de facilitarlos 𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑟 3𝑥 𝑥𝑒 𝑑𝑥 U =𝑒 3𝑥 du = 3𝑒 3𝑥 𝑥2 3𝑥 =𝑒 2 dv= xdx V= 𝑥2 2 - 𝑥𝑒 3𝑥 𝑑𝑥 𝑥 2 𝑒 3𝑥 𝑑𝑥 Existe una técnica que ayuda a identificar las funciones a las que de manera prioritaria se les asigna la letra u esta técnica se basa en la palabra ILATE el orden de prioridad es casi siempre el siguiente: I = inversa trigonométrica L= logarítmica A= algebraica T= trigonométrica E= exponencial