deber5Mnumerico

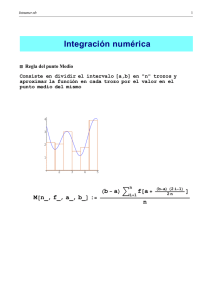
Escuela Superior Politécnica de Chimborazo
Ingeniería Automotriz
Deber No. 4
Métodos Numéricos
Dr. Mario Audelo G.
maudelo@espoch.edu.ec
27 de julio de 2020
1. Use las fórmulas de diferencia progresiva y de diferencia regresiva para determinar las aproximaciones
con que se completarán las siguientes tablas.
a)
x
0;5
0;6
0;7
f (x)
0;4794
0;5646
0;6442
b)
x
0;0
0;2
0;4
f (x)
0;00000
0;74140
0;3718
0
f (x)
0
f (x)
2. Use la fórmula de los tres puntos más conveniente para determinar las aproximaciones con que se
completarán las siguientes tablas.
0
f (x)
9;025013
11;02318
13;46374
16;44465
f (x)
a)
x
1;1
1;2
1;3
1;4
f (x)
16;94410
17;56492
18;19056
18;82091
f (x)
b)
x
8;1
8;3
8;5
8;7
f (x)
4;827866
4;240058
3;496909
2;596792
f (x)
c)
x
2;9
3;0
3;1
3;2
f (x)
3;6887983
3;6905701
3;6688192
3;6245909
f (x)
d)
x
2;0
2;1
2;2
2;3
0
0
0
1
3. Use los siguientes tiempos y posiciones para predecir la velocidad de un automovil en cada momento
incluido en la tabla.
Tiempo
0
3
5
8
10
13
Distancia 0 225 383 623 742 993
4. Aproxime las siguientes integrales aplicando la regla del trapecio.
R1
a) 0;5 x4 dx
R 0;5
b) 0 x 2 4 dx
R 1;5
c) 1 x2 ln xdx
R1
d ) 0 x2 e x dx
R
e) 04 xsin xdx
5. Repita el ejercicio 4 usando la regla de Simpson
6. Repita el ejercicio 4 usando la regla del punto medio
7. Aplique la regla compuesta del trapecio con los valores indicados de n para aproximar las siguientes
integrales
R2
a) 1 x ln xdx;
n=4
R2 3 x
b)
x e dx;
n=4
2
R2 2
dx;
n=6
c)
2 x2 +4
R5 1
d ) 3 px2 4 dx;
n=8
R 38
e) 0 tg xdx;
n=8
8. Aplique la regla compuesta de Simpson para aproximar las integrales del ejercicio 7
9. Aplique la regla compuesta del punto medio con n + 2 subintervalos para aproximar las integrales del
ejercicio 1.
R2
2
10. Aproxime 0 x2 e x dx por medio de h = 0;25:
a) Aplique la regla compuesta del trapecio
b) Aplique la regla compuesta de Simpson
c) Aplique la regla compuesta del punto medio
11. Un automovil recorre una pista de carreras en 84 s. Su velocidad en cada intervalo de 6 s se determina
mediante una pistola de radar y esta dada, en ft s 1 , desde el principio del recorrido, por los datos de
la tabla siguiente:
Tiempo
Velocidad
0
124
6
134
12
148
18
156
24
147
30
133
36
121
42
109
48
99
54
85
60
78
66
89
72
104
78
116
84
123
12. Un estudio de ingeniería del transporte requiere que se calcule el número total de autos que cruzan por
una intersección en un periodo de 24 horas. Un individuo la visita en diferentes momentos durante el
curso de un día y cuenta durante un minuto los autos que pasan por la intersección. Utilice los datos
que se resumen en la tabla para estimar el número total de autos que cruzan por día (tenga cuidado
con las unidades).
2
13. Una barra sujeta a una carga axial (véase la …gura a) se deformará como se ilustra en la curva esfuerzotensión que aparece en la …gura b). El área bajo la curva desde el esfuerzo cero hasta el punto de
ruptura se denomina módulo de rigidez del material. Proporciona una medida de la energía por unidad
de volumen que se requiere para hacer que el material se rompa. Por ello, es representativo de la
capacidad del material para superar una carga de impacto. Use integración numérica para calcular el
módulo de rigidez para la curva esfuerzo-tensión que se aprecia en la …gura b).
14. Durante un levantamiento, se le pide que calcule el área del terreno que se muestra en la …gura. Emplee
reglas de Simpson para determinar el área.
3