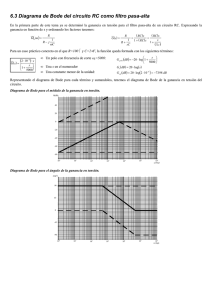
Guía práctica para construir un diagrama de Bode. Parte 1 Un diagrama de Bode es, por definición, una gráfica semilogarítmica de la magnitud (en decibeles) y de la fase (en grados) de una función de transferencia en función de la frecuencia. ¿Para qué se utilizan? Con los diagramas de Bode es posible representar gráficamente el comportamiento de un circuito eléctrico ante variaciones en la frecuencia de excitación. Es decir, cuando un circuito es sometido a señales de alimentación de frecuencia variable, se utiliza el diagrama de Bode para analizar la amplitud de la ganancia y la fase de las corrientes y los voltajes en el circuito. Los diagramas de Bode normalmente están compuestos por un diagrama de magnitud o de ganancia y un diagrama de fase, ambos dependientes de la frecuencia angular, denotada por ω. Debido a que esta frecuencia angular suele cubrir un amplio rango de valores, se acostumbra utilizar una escala logarítmica en el eje horizontal para una representación de la gráfica más fácil de analizar. En el caso del Diagrama de Magnitud, el eje vertical está formado por la ganancia del circuito, dada en decibelios (dB). En el Diagrama de Fase, el eje vertical está formado por ángulos de desfase, dados en grados. Los diagramas de Bode se construyen a partir de funciones de transferencia. Una función de transferencia es el resultado de dividir una salida entre una entrada en cualquier sistema. Por ejemplo, en el siguiente circuito: Este es un circuito RLC serie típico. De este circuito podemos obtener funciones de transferencia de voltaje, corriente y potencia, puesto que para nosotros estos son parámetros conocidos o calculables. De igual manera, se pueden obtener funciones de transferencia para cada uno de los tres elementos pasivos, sea la resistencia, el inductor o el capacitor. Por ejemplo, si se quiere obtener la función: VR (s) H(s)=---------VS (s) Es decir, la función de transferencia que relaciona el voltaje de la resistencia con la fuente de poder. El voltaje de la resistencia sería la salida, mientras que el voltaje de la fuente es la entrada. Nótese que todo está en función de «s» y esto se debe a que las funciones de transferencia se obtienen en el dominio de la frecuencia compleja. Si se pasa el circuito al dominio de la frecuencia se tiene: Si se desea obtener el voltaje en la resistencia se puede calcular la corriente I(s), para luego multiplicarla por R. A partir de esta corriente se obtiene el voltaje sobre la resistencia: Con este voltaje se puede obtener la función de transferencia H(s): En el circuito mostrado también se podrían obtener funciones de transferencia relacionando el voltaje en el inductor o en el capacitor con respecto al voltaje de la fuente, que es la única señal de entrada del circuito. No tendría caso buscar funciones de transferencia de corriente en este circuito, puesto que todos los elementos están en serie y poseen una misma corriente. También se podría calcular una función de transferencia de potencia entre cada elemento y la fuente de poder. Debido a que las funciones de transferencia relacionan una salida entre una entrada, es posible a partir de una función de transferencia calcular la ganancia de un circuito. Y es por esta razón que en el gráfico de magnitud se utilizan decibelios para expresar la magnitud de la ganancia. En los sistemas de comunicación, la ganancia se mide en bels. Históricamente, el bel se usa para medir las relación entre dos niveles de potencia o la ganancia de potencia G. El Bel es una magnitud muy grande para los sistemas con los que se trabaja comúnmente, por lo que casi siempre se trabaja con decibelios, los cuales son una décima parte de un Bel. La ganancia en decibelios se calcula utilizando: Entonces, en resumen, los diagramas de Bode son un par de gráficos que representan la ganancia de un sistema y el desfase entre una señal de salida frente a una señal de entrada. La ganancia y el ángulo de desfase se obtienen a partir de una función de transferencia, para la cual se construye el diagrama de Bode. Sin embargo, como el eje horizontal en los diagramas de Bode se utiliza una escala de frecuencia angular, esto quiere decir que las funciones de transferencia deben estar en función de la frecuencia angular y no en función de «s». Debido a que los sistemas para los cuales se hace el análisis de Bode son excitados por fuentes del tipo senoidal o cosenoidal, es posible remplazar las «s» de la función de transferencia H(s) por «jω», donde «j» es el operador imaginario (raíz cuadrada de -1) y «ω» es la frecuencia angular del sistema, dada en rad/s. Así, expresamos la función de transferencia H(s) como H(jω): Una vez se expresa la función de transferencia en función de jω se puede proceder a construir el diagrama de Bode. Construcción del diagrama de Bode: aproximación asintótica Para construir los diagramas de Bode a mano se utiliza una aproximación por medio del uso de asíntotas. Estas asíntotas se establecen con base en los polos y los ceros de la función de transferencia. La pendiente de las asíntotas depende del tipo de polos y ceros que forman la función de transferencia. Para un mejor análisis de las funciones de transferencia es conveniente factorizar tanto el numerador como el denominador, de forma tal que sea posible apreciar la forma que tienen los polos y los ceros. Este procedimiento conviene hacerlo en función de «s». De esta manera. una función de transferencia podría verse de la siguiente manera: De esta expresión se pueden identificar 7 tipos de elementos que producen 7 pendientes distintas dentro del diagrama de Bode: 1. 2. 3. 4. 5. 6. 7. Valores constantes (K) Cero en el origen (s) +−n Cero simple (s+a) Cero cuadrático (s+b)2 ó (s2+2bs+b2) Polo en el origen (s)±n Polo simple (s+c) Polo cuadrático (s+d)2 ó (s2+2ds+d2)