EJERCICIOS DE TEORIA DE CONTROL AUTOMATICO
Anuncio

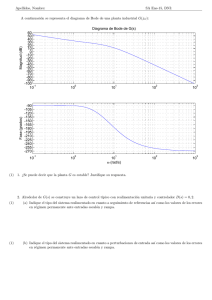
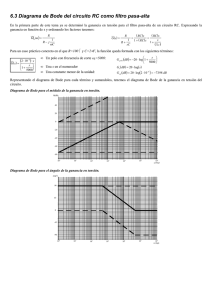
EJERCICIOS DE TEORIA DE CONTROL AUTOMATICO 1 DISEÑO DE CONTROLADORES EN DOMINIO FRECUENCIAL P2. Diseñar una red de avance para el sistema: G (s) = 200 s ( s + 2) ( s + 20) Para conseguir que la respuesta en BC tenga una sobreoscilación en torno al 15% y un error en régimen permanente ante entrada en rampa en torno al 10%. Solución: En primer lugar, ponemos la función de transferencia del sistema en forma de Bode, para dejar patente su ganancia: 5 G ( s) = s (1 + s / 2) (1 + s / 20) Por otro lado, la forma del controlador será: C ( s ) = K c (1 + τ s ) (1 + α τ s ) A partir de la especificación de error en régimen permanente: Erp rampa = 1 Kv resulta un valor requerido para Kv=10 y, por tanto, para la ganancia del controlador: Kc=2. El margen de fase requerido es: SO % ≈ 1.6 (60 − Mf ) ⇒ Mf des ≈ 50 º Dibujamos el diagrama de Bode del sistema sin compensar incluyendo la ganancia total: 10. El margen de fase que resulta con esta ganancia es de unos 13º. Por tanto, el aporte de fase que tendría que hacer la red de avance sería de: Φ m = Mf des − Mf + 10 = 47 º Como siempre, se ha añadido un margen de seguridad entre 5º y 10º. Ahora podemos calcular la “anchura” de la red de avance: α= 1 − sin Φ m = 0.15 1 + sin Φ m Para ubicar la frecuencia intermedia de la red de avance, buscamos en el Bode el punto en que la amplitud de la curva de magnitud caiga: -A dB, siendo A: A = 10 log 10 1 α = 8.5 dB El valor de -9.54 dB lo encontramos a la frecuencia: ω m ≈ 7 rad / s Con este valor, ya podemos ubicar la red de avance: τ= 1 ωm α ≈ 0 .4 Por tanto, las frecuencias “de esquina” de la red de avance son: 1 τ ≈ 2.4, 1 ατ ≈ 21.7 Dibujando la red de avance y el sistema compensado en bucle abierto, se aprecia que el margen de fase resultante es de unos 49.7º, con lo cual prácticamente satisface las especificaciones. En caso de que no hubiera sido así, tendríamos que pensar en si conviene colocar la red de avance un poco más a la izquierda o a la derecha, etc. Si nos pidieran un margen de fase bastante menor, cabría pensar que con una única red de avance no sería suficiente. M. Vargas 2005