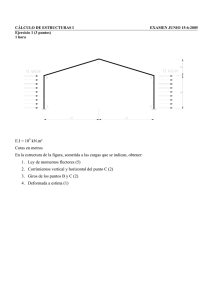
ANÁLISIS ESTRUCTURAL AVANZADO AGOSTO DICIEMBRE 2020 MÉTODO DE DISTRIBUCIÓN DE MOMENTOS. Para iniciar se requiere conocer el coeficiente de rigidez a la flexión de un elemento de longitud L, momento de inercia de su sección transversal I y tipo de material definido con su módulo de elasticidad E. se considera el elemento aislado, sin acciones y con empotramiento en ambos extremos. La rigidez es la magnitud de momento que debe de aplicarse en un extremo para provocar un giro unitario. Adoptando la convención positiva anti horario, el valor es S=4EI/L y si el extremo opuesto está articulado es 3EI/L y es cero si está libre. Si el extremo opuesto está empotrado se ocasiona un momento en este extremo, del mismo signo y de magnitud igual a ½ del momento en el 1er extremo, o sea, 2EI/L, que equivale a considerar que existe un factor de distribución de ½. En el caso de que esté articulado o libre, el valor es nulo L E I 2EI/L 4EI/L Si la estructura está integrada con el mismo tipo de material, puede asumirse el módulo de elasticidad E constante y desarrollar los métodos con las rigideces relativas 4I/L o 3I/L. El método consiste en considerar todos los extremos de la viga empotrados, calcular los momentos debidos al empotramiento, lo que puede ocasionar en elementos contiguos momentos de diferente magnitud, denominados momentos de desequilibrio, para luego utilizar la rigidez correspondiente a cada elemento para procurar el equilibrio en el apoyo. En un apoyo la distribución del momento de desequilibrio depende del factor de rigidez y es igual a Fdi = - Si/Si, tal que la suma de factores en un apoyo es igual a -1. El signo negativo es con el fin de contrarrestar el signo del momento de desequilibrio. Por otro lado, el método implica el conocer las acciones de empotramiento ocasionado por todas las acciones sobre el elemento y usar el principio de superposición para obtener los momentos finales. Las principales son: w M = wL2/12 doble empotramiento M=wL2/12 M = wL2/8 extremo articulado P 2 M=Pab /L 2 M=Pa2b/L2 a b M=Pab (a + L) / 2L2 si el extremo opuesto está articulado. Tener presente la localización de la acción P. Para poder entender estos métodos de análisis es necesario recordar en que consiste el equilibrio estático y el hiper estático. El concepto de momento flexionante, momento resistente y fuerza cortante. Convención de signos y momento de nudo/barra y barra/nudo y finalmente los tipos de apoyo en las estructuras y su relación con reacción y deformación. W= 2 t/m P=16 T Ejemplo. Nomenclatura A L=10 m EI = cte B 5m 5m A EI = cte C Convención de signos + Considerando empotrado en C Momento de empotramiento A 2 x 100 /12 16.67 Rigideces E/I Factores de distribución Factores de transporte Momento de desequilibrio 1a distribución 1er Momento de transporte Momento de desequilibrio 2a distribución 2o momento de transporte Momento de desequilibrio 3a distribución Suma de momentos de empotramiento + distribuciones + transportes (NO desequilibrios Rigideces E/I Factores de distribución Factores de distribución 0.4 0 0 B -2 x 100/12 16 x 10 /8 -16.67 20 0.4 0.4 -0.5 -0.5 0.5 0 0 -0.832 C 0.5 3.33 -0.832 -5 -5 0 0.416 0 0.832 -2.5 0.416 0 -0.208 -0.208 13.338 -23.54 23.54 0 20 -0.832 10 0 -2.5 -2.5 2.5 0 Considerando C articulado 0.4 0.4 0.3 -0.57 -0.43 0 0.5 0.5 -20 -1.665 -1.665 0 10 0 ´= - 16 (10) /8 -20 0.4 -1 0 0 0 0 Momentos de empotramiento 2 x 100 /12 -2 x 100/12 ´=Pab(a+L)/2L 2 -16.67 30 13.33 16.67 Momento de desequilibrio 1a distribución 1er traslado 0 0 -3.8 suma de momentos 12.87 0 0 0 -7.6 -5.73 0 0 0 0 -24.27 24.27 0 Cálculo de cortantes y reacciones: ´hacia arriba , negativo hacia abajo Isostáticas: apoyo 10 10 8 simple Hiperestáticas: S (24.27/10=2.43 mom en extremos / L 24.47+12.87)/10=1.14 (signo cambiado) -1.14 1.14 2.43 Cortantes 10-1.14=8.86 10+1.14=11.1 8+2.43=10.43 4 Reacciones 8.86 21.57 DIAGRAMAS DE MOMENTOS: M + : 200/8= 25 8 -2.43 8-2.43=5.57 5.57 16 X 10 / 4 = 40 25 -12.87 + -24.27 -24.27 + M efecto + 6.33 0 MEfec + 7.765 DIAGRAMA DE CORTANTES: 8.86 T 10.43 11.14 5.57 Ecuación de momentos flexionantes (a la izquierda de la sección). Para usar la función de singularidad se considera la carga uniforme de 2 t/m de B a C aplicada en ambos sentidos hacia abajo y hacia arriba manteniendo el equilibrio de acciones 16 t 2 t/ m -12.87 t-m 8.86 t 2 t/m 21.57 t X 2 t/ m 5.57 t Mx = 2 X2/2 – 12.87 – 8.86 X – 21.57 < X-10 > -2 < X-10 >2/2 + 16 < X-15 > Vx = 8.86 – 2X + 21.57 < X>10 > + 2 < X-10 > - 16 < X>15 >