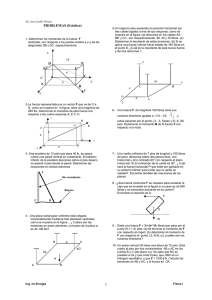
E.I = 105 kN.m² Cotas en metros En la estructura de la figura

CÁLCULO DE ESTRUCTURAS I
Ejercicio 1 (3 puntos)
1 hora
E.I = 105 kN.m²
Cotas en metros
En la estructura de la figura, sometida a las cargas que se indican, obtener:
1. Ley de momentos flectores (5)
2. Corrimientos vertical y horizontal del punto C (2)
3. Giros de los puntos B y C (2)
4. Deformada a estima (1)
EXAMEN JUNIO 15-6-2005
CÁLCULO DE ESTRUCTURAS I
Ejercicio 2 (2 puntos)
1 hora
EXAMEN JUNIO 15-6-2005
Parte 2a (1/2)
La viga en voladizo de la figura tiene una sección rectangular de dimensiones bxh. Con una carga P aplicada en el
extremo del voladizo,
A. Representar la circunferencia de Mohr del estado tensional de los siguientes puntos:
1. Un punto (A) de la fibra superior de la sección del empotramiento.
2. El centro de gravedad (B) de la sección del empotramiento.
B. ¿En qué punto de los dos anteriores se produce una mayor τmáx? ¿En qué dirección se produce?
NOTA: En sección rectangular, el módulo de las tensiones tangenciales producidas por el cortante varía
parabólicamente a lo largo del canto y tiene su valor máximo en el centro, de valor 1’5 veces el valor medio (Q/A).
Parte 2b (1/2)
La figura representa los vectores tensión determinados sobre
dos planos distintos en un mismo punto P del interior de una
laja en estado de tensión plana. Se desea conocer:
1. El ángulo β que forman ambos planos
2. Las tensiones y direcciones principales en P
CÁLCULO DE ESTRUCTURAS I
Ejercicio 3a (3 puntos)
45 minutos
Determinar:
1. Reacciones (1/10)
2. Leyes de esfuerzos en la viga (3/10)
3. Flecha en el punto C (2/10)
4. Flecha en el punto D (2/10)
5. Deformada a estima (2/10)
EXAMEN JUNIO 15-6-2005
CÁLCULO DE ESTRUCTURAS I
Ejercicio 3b (2’5 puntos)
1 hora
EXAMEN FINAL 15-6-2005
La estructura de la figura está formada por una barra vertical de longitud
L, empotrada en su extremo inferior y una barra horizontal en dirección Y de
longitud L/2, conectada rígidamente a la vertical en su extremo dorsal,
quedando contenida la estructura en el plano YZ.
En la punta de la barra horizontal se aplica una fuerza horizontal de eje X
y una vertical de eje Z, ambas de valor F. No se considera ninguna otra acción
sobre la estructura.
Se pide:
1. Esfuerzos que generan tensiones normales en la sección de
empotramiento inferior de la barra vertical (F en N, L en m).
2.
Atendiendo a las tensiones normales debidas a los esfuerzos axil y
flector en la sección de empotramiento de la barra vertical, seleccionar el perfil más adecuado de
entre los siguientes, justificadamente:
3.
Considerando una sección cuadrada hueca de dimensiones exteriores
bxb y espesor de pared b/10, obtener la expresión de la tensión normal de
mayor valor absoluto (indicando si es de tracción o de compresión), en la
sección de empotramiento de la barra vertical, función de F, b y L (b y L
en m, F en N).
4.
Si la tensión admisible del material es de ±1·109 N/m2, F vale 10 000 N
y b vale 0.1 m, obtener el valor máximo de L.
CÁLCULO DE ESTRUCTURAS I
Ejercicio 4a (2 puntos)
45 minutos
EXAMEN 2º PARCIAL 15-6-2005
Un tubo de sección octogonal de lado 2a y espesor e, de longitud indefinida, está sometido a una presión
interior de valor p.
1. Simplificar al máximo aplicando condiciones de simetría o antimetría. (3)
2. Obtener los momentos flectores máximo y mínimo por unidad de longitud en las paredes del tubo,
y los puntos de la sección del tubo en que se producen. (7)