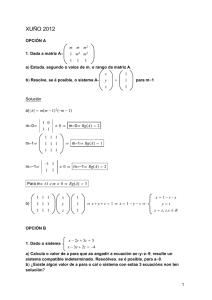
1 ED de Variables Separables. E: .y lnx/ dxD ( x y C 1) D: H

Anuncio

1
ED de Variables Separables.
E: .y ln x/
1
dy
D
dx
x
yC1
2
D: H Separamos variables e integramos:
dy
x 2 y ln x
.y C 1/2
D
)
dy D x 2 ln x dx )
dx
.y C 1/2
y
.y C 1/2
dy D
y
Z
Z
x 2 ln x dx:
Resolvemos la integral izquierda:
Z
.y C 1/2
dy D
y
Z 1
y C2C
y
dy D
y2
C 2y C ln y:
2
Resolvemos la integral derecha, por partes, usando:
1
dxI
x
x3
vD
:
3
u D ln xI
du D
dv D x 2 dxI
Z
x3
x ln x dx D
ln x
3
2
Por lo tanto
1
3
Z
x3
x dx D
3
y2
x3
C 2y C ln y D
2
3
2
ln x
1
3
ln x
1
3
C C:
C C:
Ésta es la solución general de la ED.
12. canek.azc.uam.mx: 18/ 11/ 2010