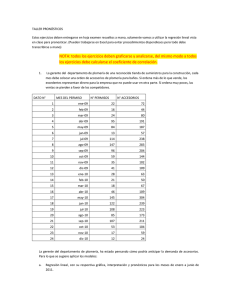
PRONOSTICO DE DEMANDA El método de mínimos cuadrados o regresión lineal se utiliza tanto para pronósticos de series de tiempo como para pronósticos de relaciones causales. En particular cuando la variable dependiente cambia como resultado del tiempo se trata de un análisis de serie temporal. En el caso por ejemplo que queramos desarrollar un pronóstico de demanda haciendo uso de la información histórica de las visitas a un determinado lugar recreacional durante los últimos 12 trimestres (3 años). Trimestres Visitas 1 2 3 4 5 6 7 8 9 10 11 12 600 1550 1500 1500 2400 3100 2600 2900 3800 4500 4000 4900 La ecuación de mínimos cuadrados para la regresión lineal es la que se muestra a continuación donde β0 y β1 son los parámetros de intercepto y pendiente, respectivamente: Estimar los valores: x y xy X2 Y2 x y xy X2 Y2 1 600 600 1 360 000 2 1 550 3 100 4 2 402 500 3 1 500 4 500 9 2 250 000 4 1 500 6 000 16 2 250 000 5 2 400 12 000 25 5 760 000 6 3 100 18 600 36 9 610 000 7 2 600 18 200 49 6 760 000 8 2 900 23 200 64 8 410 000 9 3 800 34 200 81 14 440 000 10 4 500 45 000 100 20 250 000 11 4 000 44 000 121 16 000 000 12 4 900 58 800 144 24 010 000 78 33 350 268 200 650 112 583 500 Y = 441,71+359,61X Una vez obtenido los parámetros de la regresión lineal se puede desarrollar un pronóstico de demanda (columna color azul) evaluando en la ecuación de la regresión para los distintos valores de la variable independiente (x). Por ejemplo para el primer trimestre el pronóstico es: Y (1)=441,71+359,61*1=801,3. Observación: los valores de los pronósticos han sido redondeados arbitrariamente a un decimal. Y2 Y x y xy X2 1 600 600 1 360 000 2 1 550 3 100 4 2 402 500 1,160.9 3 1 500 4 500 9 2 250 000 1,520,5 4 1 500 6 000 16 2 250 000 1,880,2 5 2 400 12 000 25 5 760 000 2,239,8 6 3 100 18 600 36 9 610 000 2,599,4 7 2 600 18 200 49 6 760 000 2,959,0 8 2 900 23 200 64 8 410 000 3,318,6 9 3 800 34 200 81 14 440 000 3,678,2 10 4 500 45 000 100 20 250 000 4,037,8 11 4 000 44 000 121 16 000 000 4,397,4 12 4 900 58 800 144 24 010 000 4,757,0 78 33 250 268 200 650 112 502 500 801,3 Siguiendo con nuestro análisis a continuación podemos desarrollar un pronóstico para los próximos 4 trimestres (un año) que corresponden a los trimestres 13, 14, 15 y 16: Y (13)=441,71+359,61*13 = 5.116,64 Y (14)=441,71+359,61*14 = 5.476,25 Y (15)=441,71+359,61*15 = 5.835,86 Y (16)=441,71+359,61*16 = 6.195,47 PROYECCION DE LA DEMANDA Un ejemplo de regresión lineal para pronosticar la demanda: Las ventas de la empresa “muerte lenta” durante los últimos 10 trimestres son las siguientes: Trimestre 1 2 3 4 5 6 7 8 9 10 11 12 Ventas 133 292 283 283 302 400 505 608 667 783 785 799 ¿Cómo pronosticar la demanda de los trimestres 13, 14 y 15 a través de un análisis de regresión lineal? SOLUCION ∑ ẋ ŷ Periodo (x) Demanda (y) xy 𝒙𝟐 𝒚𝟐 Pronostico(Y) 1 2 3 4 5 6 7 8 9 10 11 12 133 292 283 283 302 400 505 608 667 783 785 799 133 584 849 1132 1510 2400 3535 4864 6003 7830 8635 9588 47063,0 1 4 9 16 25 36 49 64 81 100 121 144 650,0 17689 341056 80089 80089 91204 160000 255025 369664 444889 613089 616225 638401 3451628,0 137 200 264 328 391 455 518 582 646 709 773 837 6.5 486,7 𝟒𝟕𝟎𝟔𝟑,𝟎−𝟏𝟐(𝟔,𝟓)(𝟒𝟖𝟔,𝟕) 𝟔𝟓𝟎,𝟎−𝟏𝟐(𝟔,𝟓𝟐 ) = 63,64 y= 486,7 b= x=6.5 a= 486,7 – 63,657(6,5) = 72,929 n= 𝒀𝟏𝟑= 900,44 10 ∑𝒙𝟐 = 650 𝒀𝟏𝟒= 964,09 ∑xy = 𝒀𝟏𝟓= 1027,75 3451628,0 Una medida apropiada para medir el error en regresión lineal es el error estándar de estimación (Sy,x), que nos permite determinar la variabilidad en torno a la recta de regresión. Con los datos obtenidos en nuestra tabla, reemplazamos en la formula y obtenemos: Error estándar del estimado Sy,x: = 54,79 Esto lo interpretamos como una medida de la variabilidad o dispersión de los valores observados alrededor de nuestra línea de regresión. Otro análisis que si o si debemos realizar cuando trabajamos con un análisis de regresión, no importa si es con un fin de pronóstico, es el cálculo del coeficiente de correlación. Como lo dijimos anteriormente, el coeficiente de correlación dará una medida de asociación entre las variables X y Y. Dicho de otra forma, el coeficiente correlación en la división entre la covarianza y el producto de las desviaciones estándar de ambas variables. Así pues, si queremos ver la correlación entre la demanda y lo pronosticado en periodos anteriores (desde el periodo 1 hasta el 12), El resultado de este ejercicio es r = 0,975 . Esto indica que la correlación es muy fuerte y positiva porque está cercana a 1. En otras palabras, nos conviene seguir usando este método de pronóstico para futuros períodos. RESOLVER LOS SIGUIENTES EJERCICICIOS 2.- En la localidad de Tarapoto se recopilo información a través del método de preferencia declarada sobre las visitas realizadas a lugar turístico denominado La Laguna Azul durante los últimos 12 trimestres (3 años), con la finalidad de proyectar las visitas para los próximo 4 trimestres; la información se muestra en la tabla adjunta: trimestre 1 2 3 4 5 6 7 8 9 10 11 12 ventas 2600 2500 2500 3500 2400 3100 3600 3900 3800 4500 4000 4900 Interpretar el error estándar de estimación Calcular e interpretar el coeficiente de correlación 3.- Una cadena de Pizzerías toma una muestra de diez de sus sucursales para tratar de encontrar un modelo matemático que le permita predecir sus ventas y obtuvo los siguientes datos: la población de personas en miles fue de 2, 6, 8, 8, 12, 16, 20, 20, 22, 26; y las ventas trimestrales en miles de pesos fue de: 58, 105, 88, 118, 117, 137, 157, 169, 169, 149, 202. Realice una regresión para estimar las ventas de dos sucursales que tienen 14,000 y 30,000 personas como potenciales clientes respectivamente Interpretar el error estándar de estimación Calcular e interpretar el coeficiente de correlación