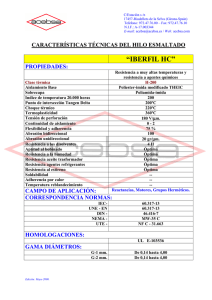
NOTA: EJERCICIOS PROPUESTOS Apellidos Semestre Nombres Ciclo Escuela Aula Asignatura Toma de decisiones Turno Docente Pérez Ruibal Regalado Eliana Fecha 1.- Resuelva el programa lineal mediante el procedimiento de solución gráfica: Max 5A + 5B s.a. 1A ≤100 1B ≤ 80 2 A + 4B ≤ 400 A,B ≥ 0 2.-Identifique la región factible para el conjunto de restricciones siguiente: 3 A + 2B ≥ 0 2 A +1B ≤ 200 1A ≤ 150 A,B ≥ 0 3 A + 2B = 0 2 A +1B = 200 1A = 150 *3 A + 2B = 0 3(0) + 2B = 0 2B = 0 B=0 3 A + 2B = 0 3A + 2(0) = 0 3A = 0 A=0 A=0 B=0 Firma del estudiante señalando la conformidad del calificativo. TOMA DE DECISIONES 2020 – II M T N *2A + 1B = 200 2(0) + 1B = 200 1B = 200 B = 200 2A + 1B = 200 2A + 1(0) = 200 2A = 200 B = 100 A=0 *1A + 1B = 150 1(0) + 1B = 150 1B = 150 B = 150 1A + 1B = 150 1A + 1(0) = 150 1A = 150 A = 150 A=0 LOS VÉRTICES SON: *(0,0) *(200,100) *(150,150) B=0 B=0 3.- Considere el problema de programación lineal: Max 3 A + 3B s.a. 2 A +4B ≤ 12 6 A + 4B≤ 24 A,B ≥ 0 a) Encuentre la solución óptima mediante la solución gráfica. b) Si la función objetivo se cambia a 2 A +6B, ¿Cuál sería la solución óptima? 4) Un taller tiene tres (3) tipos de máquinas A, B y C; puede fabricar dos (2) productos 1 y 2, todos los productos tienen que ir a cada máquina y cada uno va en el mismo orden: Primero a la máquina A, luego a la B y luego a la C. La siguiente tabla muestra: Las horas requeridas en cada máquina, por unidad de producto Las horas totales disponibles para cada máquina, por semana La ganancia por unidad vendida de cada producto Formule y resuelva a través del método gráfico un modelo de Programación Lineal para la situación anterior que permite obtener la máxima ganancia para el taller.