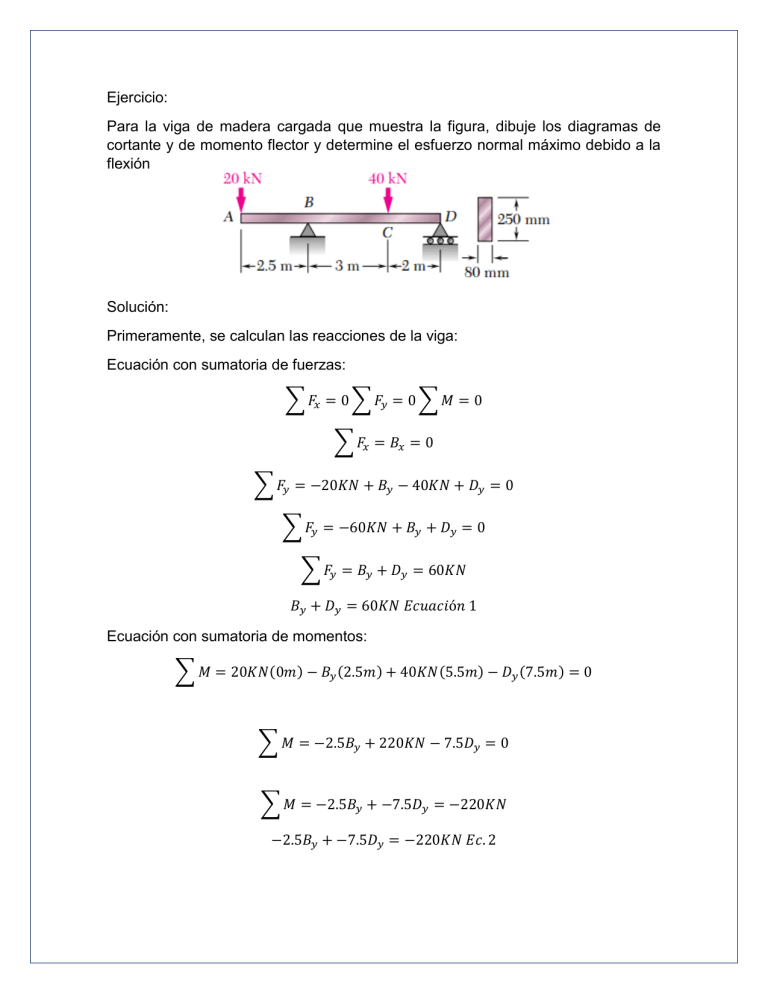
Ejercicio: Para la viga de madera cargada que muestra la figura, dibuje los diagramas de cortante y de momento flector y determine el esfuerzo normal máximo debido a la flexión Solución: Primeramente, se calculan las reacciones de la viga: Ecuación con sumatoria de fuerzas: ∑ 𝐹𝑥 = 0 ∑ 𝐹𝑦 = 0 ∑ 𝑀 = 0 ∑ 𝐹𝑥 = 𝐵𝑥 = 0 ∑ 𝐹𝑦 = −20𝐾𝑁 + 𝐵𝑦 − 40𝐾𝑁 + 𝐷𝑦 = 0 ∑ 𝐹𝑦 = −60𝐾𝑁 + 𝐵𝑦 + 𝐷𝑦 = 0 ∑ 𝐹𝑦 = 𝐵𝑦 + 𝐷𝑦 = 60𝐾𝑁 𝐵𝑦 + 𝐷𝑦 = 60𝐾𝑁 𝐸𝑐𝑢𝑎𝑐𝑖ó𝑛 1 Ecuación con sumatoria de momentos: ∑ 𝑀 = 20𝐾𝑁(0𝑚) − 𝐵𝑦 (2.5𝑚) + 40𝐾𝑁(5.5𝑚) − 𝐷𝑦 (7.5𝑚) = 0 ∑ 𝑀 = −2.5𝐵𝑦 + 220𝐾𝑁 − 7.5𝐷𝑦 = 0 ∑ 𝑀 = −2.5𝐵𝑦 + −7.5𝐷𝑦 = −220𝐾𝑁 −2.5𝐵𝑦 + −7.5𝐷𝑦 = −220𝐾𝑁 𝐸𝑐. 2 Resolver sistemas de ecuaciones: 𝐵𝑦 + 𝐷𝑦 = 60𝐾𝑁 𝐸𝑐𝑢𝑎𝑐𝑖ó𝑛 1 −2.5𝐵𝑦 ± 7.5𝐷𝑦 = −220𝐾𝑁 𝐸𝑐𝑢𝑎𝑐𝑖ó𝑛 2 Determinantes: 1 1 ) = −7.5 − (−2.5) = −7.5 + 2.5 −2.5 −7.5 𝐷∆ = ( 𝐷∆ = −5 𝐷𝑥 = ( 60 −220 1 ) = −450 − (−220) = −450 + 220 −7.5 𝐷∆ = −230 1 60 𝐷𝑦 = ( ) = −220 − (−150) = −220 + 150 −2.5 −220 𝐷∆ = −70 𝐵𝑦 = 𝐵𝑦 = 𝐷𝑥 𝐷∆ 𝐷𝑦 = 𝐷𝑦 𝐷∆ −230 −70 𝐷𝑦 = −5 −5 𝐵𝑦 = 46 𝐾𝑁 𝐷𝑦 = 14 𝐾𝑁 Determinar las fuerzas cortantes y el momento flector: Corte 1: +↑ ∑ 𝐹𝑦 = 0 +↑ ∑ 𝐹𝑦 = −20 − 𝑉1 = 0 +↑ ∑ 𝐹𝑦 = −𝑉1 = 20 −𝑉1 = 20 𝑉1 = −20𝐾𝑁 +⃔ ∑ 𝑀 = 0 +⃔ ∑ 𝑀 = (20𝐾𝑁)(0𝑚) + 𝑀1 = 0 +⃔ ∑ 𝑀 = 𝑀1 = 0 𝑀1 = 0𝐾𝑁𝑚 Corte 2: +↑ ∑ 𝐹𝑦 = 0 +↑ ∑ 𝐹𝑦 = −20 − 𝑉2 = 0 +↑ ∑ 𝐹𝑦 = −𝑉2 = 20 −𝑉2 = 20 𝑉2 = −20 +⃔ ∑ 𝑀 = 0 +⃔ ∑ 𝑀 = (20𝐾𝑁)(2.5𝑚) + 𝑀2 = 0 +⃔ ∑ 𝑀 = 50𝐾𝑁𝑚 + 𝑀2 = 0 +⃔ ∑ 𝑀 = +𝑀2 = −50𝐾𝑁𝑚 𝑀2 = −50𝐾𝑁𝑚 Corte 3: +↑ ∑ 𝐹𝑦 = 0 +↑ ∑ 𝐹𝑦 = −20𝐾𝑁 + 46𝐾𝑁 − 𝑉3 = 0 +↑ ∑ 𝐹𝑦 = 26𝐾𝑁 − 𝑉3 = 0 +↑ ∑ 𝐹𝑦 = −𝑉3 = −26𝐾𝑁 −𝑉3 = −26𝐾𝑁 𝑉3 = 26𝐾𝑁 +⃔ ∑ 𝑀 = 0 +⃔ ∑ 𝑀 = (20𝐾𝑁)(2.5𝑚) − (46𝐾𝑁)(0𝑚) + 𝑀3 = 0 +⃔ ∑ 𝑀 = 50𝐾𝑁𝑚 − 0 + 𝑀3 = 0 +⃔ ∑ 𝑀 = 𝑀3 = −50𝐾𝑁𝑚 𝑀3 = −50𝐾𝑁𝑚 Corte 4: +↑ ∑ 𝐹𝑦 = 0 +↑ ∑ 𝐹𝑦 = −20𝐾𝑁 + 46𝐾𝑁 − 𝑉4 = 0 +↑ ∑ 𝐹𝑦 = 26𝐾𝑁 − 𝑉4 = 0 +↑ ∑ 𝐹𝑦 = −𝑉4 = −26𝐾𝑁 −𝑉4 = −26𝐾𝑁 𝑉4 = 26𝐾𝑁 +⃔ ∑ 𝑀 = 0 +⃔ ∑ 𝑀 = (20𝐾𝑁)(5.5𝑚) − (46𝐾𝑁)(3𝑚) + 𝑀4 = 0 +⃔ ∑ 𝑀 = 110𝐾𝑁𝑚 − 138𝐾𝑁𝑚 + 𝑀4 = 0 +⃔ ∑ 𝑀 = −28𝐾𝑁𝑚 + 𝑀4 = 0 +⃔ ∑ 𝑀 = 𝑀4 = 28𝐾𝑁𝑚 𝑀4 = 28 𝐾𝑁𝑚 Corte 5: +↑ ∑ 𝐹𝑦 = 0 +↑ ∑ 𝐹𝑦 = −20𝐾𝑁 + 46𝐾𝑁 − 40𝐾𝑁 − 𝑉5 = 0 +↑ ∑ 𝐹𝑦 = −14𝐾𝑁 − 𝑉5 = 0 +↑ ∑ 𝐹𝑦 = −𝑉5 = 14𝐾𝑁 −𝑉5 = 14𝐾𝑁 𝑉5 = −14 𝐾𝑁 +⃔ ∑ 𝑀 = 0 +⃔ ∑ 𝑀 = (20𝐾𝑁)(5.5𝑚) − (46𝐾𝑁)(3𝑚) + (40𝐾𝑁)(0𝑚) + 𝑀5 = 0 +⃔ ∑ 𝑀 = 110𝐾𝑁𝑚 − 138𝐾𝑁𝑚 + 0 + 𝑀5 = 0 +⃔ ∑ 𝑀 = −28𝐾𝑁𝑚 + 𝑀5 = 0 +⃔ ∑ 𝑀 = 𝑀5 = 28𝐾𝑁𝑚 𝑀5 = 28 𝐾𝑁𝑚 Corte 6: +↑ ∑ 𝐹𝑦 = 0 +↑ ∑ 𝐹𝑦 = −20𝐾𝑁 + 46𝐾𝑁 − 40𝐾𝑁 − 𝑉6 = 0 +↑ ∑ 𝐹𝑦 = −14𝐾𝑁 − 𝑉6 = 0 +↑ ∑ 𝐹𝑦 = −𝑉5 = 14𝐾𝑁 −𝑉6 = 14𝐾𝑁 𝑉6 = −14 𝐾𝑁 +⃔ ∑ 𝑀 = 0 +⃔ ∑ 𝑀 = (20𝐾𝑁)(7.5𝑚) − (46𝐾𝑁)(5𝑚) + (40𝐾𝑁)(2𝑚) + 𝑀5 = 0 +⃔ ∑ 𝑀 = 150𝐾𝑁𝑚 − 230𝐾𝑁𝑚 + 80𝐾𝑁𝑚 + 𝑀6 = 0 +⃔ ∑ 𝑀 = −80𝐾𝑁𝑚 + 80𝐾𝑁𝑚 + 𝑀6 = 0 +⃔ ∑ 𝑀 = 0 + 𝑀6 = 0𝐾𝑁𝑚 𝑀6 = 0 𝐾𝑁𝑚 Esfuerzo normal máximo: Ocurre en B, donde |M| es máximo. Se utiliza la ecuación planteada a continuación para obtener el módulo de sección. Sustituyendo este valor y |𝑀| = |𝑀𝐵 | = 50𝑋103 𝑁. 𝑚 en la ecuación siguiente. 𝐸𝑠𝑓𝑢𝑒𝑟𝑧𝑜 𝑛𝑜𝑟𝑚𝑎𝑙 𝑑𝑒 𝑙𝑎 𝑣𝑖𝑔𝑎: 60.0 𝑀𝑃𝑎 Comparar resultados con el software de simulación de vigas MD SOLID:





![Prueba Segundos2[1]](http://s2.studylib.es/store/data/003397536_1-3ac4e8618b6474fb10e9bb3037bc9dd2-300x300.png)