CÁLCULO DE EJES
PROBLEMA 17.
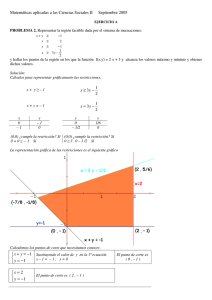
La figura 1 muestra el eje de una lijadora de disco, fabricada en acero, que tiene una tensión de rotura σ u=900
MPa y una tensión de fluencia σyp=750 MPa. El eje pasa de tener un diámetro de 16 mm a otro de 18 mm a
través de un radio de acuerdo de 5 mm. El límite de fatiga del eje es 290 MPa. La carga más severa ocurre
cuando se aplica un objeto (que se considera puntual) cerca de la periferia del disco (a 100 mm del centro del
eje), con fuerza suficiente para desarrollar un par de torsión de fricción de 12 Nm en el eje. El coeficiente de
fricción entre el objeto y el disco es de 0,6. Para estas condiciones descritas, se pide calcular el coeficiente de
seguridad del eje a vida infinita.
SOLUCIÓN:
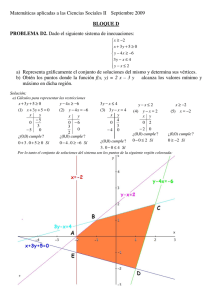
Se da comienzo a la resolución identificando las fuerzas inherentes a la operación de pulido: el objeto se pule
debido a la fuerza de rozamiento existente en el contacto con el disco-lija.
T = 12 Nm = 12000 Nmm = µxFx100 = 0,6xFx100 → F=200 N ; µxF = 0,6x200 = 120N
Cálculo de los esfuerzos:
Diagramas de esfuerzos:
Cálculo de las tensiones:
Coeficientes de concentración de tensiones:
PROBLEMA 18.
Un eje está cargado con un momento flexionante y un par torsor de manera que: 𝑀𝑎 = 600 𝑙𝑏𝑓 ∙
𝑖𝑛, 𝑇𝑎 = 400 𝑙𝑏𝑓 ∙ 𝑖𝑛, 𝑀𝑚 = 500 𝑙𝑏𝑓 ∙ 𝑖𝑛 𝑦 𝑇𝑚 = 300 𝑙𝑏𝑓 ∙ 𝑖𝑛. Para el eje: 𝑆𝑢 = 100 𝑘𝑝𝑠𝑖, 𝑆𝑦 =
80 𝑘𝑝𝑠𝑖, y se puede asumir una resistencia límite a la fatiga 𝑆𝑒 = 30 𝑘𝑝𝑠𝑖. Suponiendo que: 𝐾𝑓 =
2.2, 𝐾𝑓𝑠 = 1.8 𝑦 𝐹𝑆 = 2. Determine el diámetro mínimo aceptable según: Gerber, Soderberg y
Goodman. Comente los resultados.
Solución:
a) Según el criterio de Gerber:
1
1
8𝐴
2𝐵𝑆𝑒 2 2
=
{1
+
[1
+
(
) ] }
𝑛 𝜋𝑑3 𝑆𝑒
𝐴𝑆𝑢𝑡
1
3
1
2 2
8𝑛𝐴
2𝐵𝑆𝑒
𝑑=(
{1 + [1 + (
) ] })
𝜋𝑆𝑒
𝐴𝑆𝑢𝑡
Donde:
2
𝐴 = √4(𝐾𝑓 𝑀𝑎 ) + 3(𝐾𝑓𝑠 𝑇𝑎 )
2
2
𝐵 = √4(𝐾𝑓 𝑀𝑚 ) + 3(𝐾𝑓𝑠 𝑇𝑚 )
2
Sustituyendo los datos en las ecuaciones anteriores tenemos que:
2
2
2
2
𝐴 = √4 ∙ (2.2 ∙ 600 𝑙𝑏𝑓 ∙ 𝑖𝑛) + 3 ∙ (1.8 ∙ 400 𝑙𝑏𝑓 ∙ 𝑖𝑛) = 2919.73 𝑙𝑏𝑓 ∙ 𝑖𝑛
𝐵 = √4 ∙ (2.2 ∙ 500 𝑙𝑏𝑓 ∙ 𝑖𝑛) + 3 ∙ (1.8 ∙ 300 𝑙𝑏𝑓 ∙ 𝑖𝑛) = 2390.56 𝑙𝑏𝑓 ∙ 𝑖𝑛
2
𝑙𝑏𝑓
2
∙
𝑙𝑏
∙
𝑖𝑛)
∙
(30000
)
(2390.56
𝑓
(8) ∙ (2) ∙ (2913.73 𝑙𝑏𝑓 ∙ 𝑖𝑛)
𝑖𝑛2
𝑑=
∙ √1 + [1 + (
)]
𝑙𝑏𝑓
𝑙𝑏𝑓
𝜋 ∙ (30000 2 )
(2919.73 𝑙𝑏𝑓 ∙ 𝑖𝑛) ∙ (100000 2 )
𝑖𝑛
𝑖𝑛
√
3
𝒅 = 𝟏. 𝟏𝟎𝟐 𝒊𝒏
b) Según el criterio de Soderberg:
3
𝑑 = √[
16 ∙ 𝑛 𝐴2 𝐵 2
∙ √ 2 + 2]
𝜋
𝑆𝑒 𝑆𝑦
Sustituyendo los valores ya conocidos en la ecuación anterior:
2
2
(16) ∙ (2) (2919.73 𝑙𝑏𝑓 ∙ 𝑖𝑛)
(2390.56 𝑙𝑏𝑓 ∙ 𝑖𝑛)
𝑑=√
∙√
+
= 1.012 𝑖𝑛
2
𝜋
𝑙𝑏𝑓
𝑙𝑏𝑓 2
(30000 2 )
(80000 2 )
𝑖𝑛
𝑖𝑛
[
]
3
𝒅 = 𝟏. 𝟎𝟏𝟐 𝒊𝒏
c) Según el criterio de Goodman:
3
𝑑 = √[
16 ∙ 𝑛 𝐴
𝐵
( +
)]
𝜋
𝑆𝑒 𝑆𝑢𝑡
Sustituyendo los valores ya conocidos en la ecuación anterior:
3
(16) ∙ (2) 2919.73 𝑙𝑏𝑓 ∙ 𝑖𝑛 2390.56 𝑙𝑏𝑓 ∙ 𝑖𝑛
𝑑 = √[
(
+
)]
𝑙𝑏𝑓
𝑙𝑏𝑓
𝜋
30000 2
100000 2
𝑖𝑛
𝑖𝑛
𝒅 = 𝟏. 𝟎𝟕𝟑 𝒊𝒏
Comentario
Se deben comparar todos los resultados obtenidos. Específicamente, deben compararse los resultados
obtenidos mediante de criterio Soderberg y Goodman con respecto al resultado obtenido con el criterio de
Gerber. Esto puede mostrarse en la siguiente tabla:
Criterio
d (in)
Comparación con el criterio de
Gerber
Gerber
1.102
Soberberg
1.012
8.2% menor
Menos
conservadora
Goodman
1.073
2.6% menor
Menos
conservadora
PROBLEMA 19.
𝐷
La sección del eje mostrado en la Figura será diseñado de manera tal que 𝑑 = 0.75𝐷 y 𝑟 = 20,
donde el diámetro 𝑑 debe ser maquinado a un tamaño comercial, es decir, que se pueda alojar
en un cojinete de contacto rodante. El material del eje s SAE – 2340, tratado térmicamente hasta
obtener una resistencia última a la tensión de 1226 MPa y una resistencia a la fluencia de 1130
MPa, con una dureza no menor de 318 HB. El eje se encuentra sometido a un momento
flexionante de 70 N∙m. Use un factor de seguridad de 2.5 y dimensione el eje para una vida
infinita.
Solución:
Este problema debe resolverse por iteraciones, donde 𝑆𝑒 viene en función del tamaño del eje.
El material empleado es SAE 2340 cuyas propiedades mecánicas son las siguientes: 𝑆𝑢𝑡 =
1226 𝑀𝑃𝑎, 𝑆𝑦 = 1130 𝑀𝑃𝑎 𝑦 𝐻𝐵 ≥ 368.
El factor de superficie 𝐾𝑎 viene dado por la siguiente ecuación:
𝑏
𝐾𝑎 = 𝑎 ∙ 𝑆𝑢𝑡
Para un material maquinado y laminado en frío, como es el caso del material con el que
estamos tratando, las constante a y b tienen los siguiente valores: 𝑎 = 4.51 𝑀𝑃𝑎 𝑦 𝑏 = −0.265.
Sustituyendo estos valores en la ecuación anterior, tenemos que:
𝐾𝑎 = (4.51) ∙ (1226 𝑀𝑃𝑎)−0.265 = 0.685
a) Primera iteración:
Eligiendo 𝑑𝑟 = 22 𝑚𝑚
Factor de tamaño 𝐾𝑏 . El factor de tamaño 𝐾𝑏 viene dado por la siguiente relación:
𝑑 −0.107
𝐾𝑏 = (
)
7.62
Sustituyendo valores:
22 𝑚𝑚 −0.107
𝐾𝑏 = (
)
= 0.893
7.62
𝐾𝑏 = 0.893
De la ecuación de Marin, tenemos que: 𝑆𝑒 = 𝑘𝑎 ∙ 𝐾𝑏 ⋅ 𝐾𝑐 ∙ 𝐾𝑑 ∙ 𝐾𝑓 ∙ 𝑆𝑒,
Sustituyendo: 𝑆𝑒 = (0.685) ∙ (0.893) ∙ (0.5) ∙ (1226) = 374.98 𝑀𝑃𝑎
𝑆𝑒 = 374.98 𝑀𝑃𝑎
𝑑𝑟 = 𝑑 − 2𝑟; 𝑑𝑟 = 0.75𝐷 −
2𝐷
= 0.65𝐷
20
𝐷=
𝑑𝑟
22 𝑚𝑚
=
= 33.8 𝑚𝑚
0.65
0.65
𝑟=
𝐷
33.8 𝑚𝑚
=
= 1.69 𝑚𝑚
20
20
Cálculo de 𝐾𝑡 . De la siguiente Figura: (Figura 1)
𝑑 = 𝑑𝑟 + 2𝑟; 𝑑 = 22 𝑚𝑚 + 2 ∙ (1.69 𝑚𝑚) = 25.4 𝑚𝑚
𝑑
25.4 𝑚𝑚
=
= 1.15
𝑑𝑟
22 𝑚𝑚
𝑟
1.69 𝑚𝑚
=
= 0.077 𝐾𝑡 = 1.9
𝑑𝑟
22 𝑚𝑚
Cálculo de 𝐾𝑡𝑠 .
Para calcular este factor, debe usarse la siguiente Figura: (Figura 2)
Donde de acuerdo a los resultados obtenidos previamente tenemos que:
𝐾𝑡𝑠 = 1.5
(𝑉𝑎𝑙𝑜𝑟 𝑎𝑝𝑟𝑜𝑥𝑖𝑚𝑎𝑑𝑜 𝑜𝑏𝑡𝑒𝑛𝑖𝑑𝑜 𝑑𝑒 𝑙𝑎 𝐹𝑖𝑔𝑢𝑟𝑎 𝑎𝑛𝑡𝑒𝑟𝑖𝑜𝑟)
Por la siguiente Figura: (Figura 3)
Se obtiene el valor para 𝑟 𝑦 𝑞
𝑟 = 1.69 𝑚𝑚 𝑞 = 0.90
Por medio de la siguiente figura: (Figura 4)
Se obtiene el valor de 𝑟 𝑦 𝑞𝑠
𝑟 = 1.69 𝑚𝑚
𝑞𝑠 = 0.97
Por las siguiente ecuaciones, obtenemos los valores para 𝐾𝑓 𝑦 𝐾𝑓𝑠
𝐾𝑓 = 1 + 𝑞 ∙ (𝐾𝑡 − 1)
𝐾𝑓𝑠 = 1 = 𝑞𝑠 ∙ (𝐾𝑡𝑠 − 1)
Sustituyendo:
𝐾𝑓 = 1 + 0.90 ∙ (1.9 − 1) = 1.81
𝐾𝑓𝑠 = 1 + 0.97 ∙ (1.5 − 1) = 1.49
De acuerdo al criterio ASME de falla:
𝐾𝑓 ∙ 𝑀𝑎 2
𝐾𝑓𝑠 ∙ 𝑇𝑚
16 ∙ 𝑛
𝑑= √
[4 ∙ (
) +3∙(
)]
𝜋
𝑆𝑒
𝑆𝑦
3
Sustituyendo valores:
1
(16) ∙ (2)
(1.81) ∙ (70) ∙ (103 )
(1.49) ∙ (45) ∙ (103 ) 2
𝑑 = √(
∙ [4 ∙ (
)+3∙(
)] )
𝜋
375
1130
3
𝑑 = 20.6 𝑚𝑚
b) Segunda iteración:
Seleccionado 𝑑𝑟 = 20.6 𝑚𝑚
20.6 𝑚𝑚 −0.107
𝐾𝑏 = (
)
= 0.899
7.62
𝑆𝑒 = (0.685) ∙ (0.899) ∙ (0.5) ∙ (1226) = 3775.5 𝑀𝑃𝑎
𝐷=
𝑑𝑟
20.6 𝑚𝑚
=
= 31.7 𝑚𝑚
0.65
0.65
𝑟=
𝐷
31.7 𝑚𝑚
=
= 1.59 𝑚𝑚
20
20
De la Figura 1 y 2 ya mostradas con anterioridad, tenemos que:
𝑑 = 𝑑𝑟 + 2𝑟;
𝑑 = 20.6 𝑚𝑚 + 2 ∙ (1.59 𝑚𝑚);
𝑑 = 23.8 𝑚𝑚
𝑑
23.8 𝑚𝑚
=
= 1.16
𝑑𝑟
20.6 𝑚𝑚
𝑟
1.59
=
= 0.077
𝑑𝑟
20.6
Según las figuras ya mostradas (Figuras 3, 4 y 5) obtenemos los siguientes valores:
𝐾𝑡 = 1.9
𝐾𝑡𝑠 = 1.5
𝑞 = 0.9
𝑞𝑠 = 0.97
𝐾𝑓 = 1.81
𝐾𝑓𝑠 = 1.49
Empleando nuevamente la ecuación ASME de falla, es decir, la ecuación:
3 16 ∙ 𝑛
𝐾𝑓 ∙ 𝑀𝑎 2
𝐾𝑓𝑠 ∙ 𝑇𝑚
𝑑= √
[4 ∙ (
) +3∙(
)]
𝜋
𝑆𝑒
𝑆𝑦
Con los nuevos valores obtenidos en esta iteración obtenemos:
1
(16) ∙ (2)
(1.81) ∙ (70) ∙ (103 )
(1.49) ∙ (45) ∙ (103 ) 2
𝑑 = √(
∙ [4 ∙ (
)+3∙(
)] )
𝜋
375
1130
3
𝑑 = 20.6 𝑚𝑚
Es decir, no se ha producido cambio alguno en lo dimensional.
Finalmente:
𝐷=
20.6 𝑚𝑚
= 31.7 𝑚𝑚
0.65
𝑑 = 0.75 ∙ (31.7 𝑚𝑚) = 23.77 𝑚𝑚
Se usarán los valores definitivos de: 𝐷 = 32 𝑚𝑚, 𝑑 = 24 𝑚𝑚 𝑦 𝑟 = 1.6 𝑚𝑚