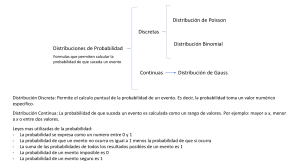
Modelación de las llegadas (Procesos de Poisson) Profesor: Yerko Sánchez Simulación de Sistemas Motivación Objetivo de la clase: • Presentar las principales Distribuciones de Probabilidad que modelan algunos procesos. • Identificar un proceso de Conteo. • Conocer las propiedades de un Proceso de Poisson como un caso particular del Proceso de Conteo. • Identificar las Distribuciones de Probabilidad asociadas al Procesos de Poisson. Introducción Dado que las actividades y fenómenos en general presentan una estructura estocástica (no existe certeza sobre su comportamiento), su representación en un modelo estocástico debe ser mediante distribuciones estadísticas. Introducción • Los datos recolectados deben ser analizados para proponer una hipótesis sobre su posible distribución estadística. • Ejemplo: Los datos pueden ser representados por una distribución Normal con una media de 10 y una Desviación Estándar de 2 Introducción La hipótesis se puede realizar con el apoyo de: • Estadísticas descriptivas. • Histogramas. • Sugeridas por el tipo de proceso. Estadísticas Descriptivas • • • • • • Media Desviación estándar Mediana Moda Curtosis Coeficiente de asimetría Estadísticas Descriptivas • Distribución Normal – media≈moda≈mediana – Coef. Asimetría≈0 – Curtosis≈0 • Distribución Exponencial – Media≈Desv. Estándar – Curtosis positivo • Distribuciones con cola hacia la derecha – Curtosis positivo – Gamma, Erlang, Weibull*, Exponencial, Lognormal…. • En simulación la mayoría de las distribuciones tienen esta forma. *dependiendo los parámetros la cola puede ir hacia la izquierda. Histogramas (Distribuciones típicas) Características sugeridas del Proceso • Selección de familia de distribuciones – Se sugiere a partir de la forma del histograma – Información relativa al proceso del cual los datos fueron recolectados: • Exponencial: Tiempo entre llegadas. • Poisson: Número de eventos por unidad de tiempo • Erlang: Suma de distribuciones exponenciales i.i.d. (Independiente e idénticamente distribuidas). Por ej: tiempo que transcurre hasta la k-ésima llegada. • Weibull: Tiempo entre fallas. • Normal: Suma de un número de procesos compuestos (líneas de ensamble). Definición: Proceso de Conteo 𝑆𝑒𝑎 𝑁 𝑡 , 𝑡 ≥ 0 𝑒𝑠 𝑢𝑛 𝑝𝑟𝑜𝑐𝑒𝑠𝑜 𝑑𝑒 𝑐𝑜𝑛𝑡𝑒𝑜 𝑠𝑖 𝑁 𝑡 𝑒𝑠 𝑢𝑛𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑎𝑙𝑒𝑎𝑡𝑜𝑟𝑖𝑎 𝑞𝑢𝑒 𝑐𝑜𝑟𝑟𝑒𝑠𝑝𝑜𝑛𝑑𝑒 𝑎𝑙 𝑛ú𝑚𝑒𝑟𝑜 𝑑𝑒 𝑒𝑣𝑒𝑛𝑡𝑜𝑠 𝑞𝑢𝑒 ℎ𝑎𝑛 𝑜𝑐𝑢𝑟𝑟𝑖𝑑𝑜 𝑒𝑛 𝑒𝑙 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑜[0, 𝑡] Ejemplo de Procesos que son de conteo: Número de llamadas telefónicas recibidas [0, t] Número de personas que han ingresado a un recinto en [0, t] Número de accidentes de tránsito ocurridos en [0, t] Ejemplo de Procesos que No son de conteo: Número de personas en la sala en el instante t. Número de líneas telefónicas ocupadas en el instante t. Propiedades de los Procesos de Conteo: N(t) es siempre un entero no negativo. Si el instante s < t, entonces N(s)≤N(t) (es no decreciente) El número de eventos en el intervalo (s, t] está dado por N(t)-N(s) Además, se pueden tener las siguientes propiedades: Incrementos independientes (i.i.) Los eventos ocurridos en intervalos disjuntos de tiempo, son independientes entre sí. Incrementos estacionarios (i.e) La probabilidad de ocurrencia de eventos en un intervalo de tiempo depende sólo del tamaño del intervalo. Propiedad de Orden Los eventos cumplen con la ocurrencia de orden en el tiempo. Distribución de Poisson 𝑥 (𝑡 ∙ λ) 𝑒 −𝑡λ 𝑃 𝑡, 𝑥 = 𝑥! Donde: P(t, x): Corresponde a la función de probabilidad Poisson. 𝜆: Es la media de la Distribución de Poisson [eventos/tiempo] t: Factor para convertir λ a las unidades de tiempo correspondiente. x: Es la variable aleatoria discreta 0,1,2,…n. 𝑥 (λ) 𝑒 −λ 𝑃 𝑥 = 𝑥! Proceso de Poisson Incrementos Independientes: Los eventos ocurridos en intervalos disjuntos de tiempo, son independientes entre sí. Ej: La llegada de autos a un estacionamiento se puede representar como un Proceso de Poisson de tasa λ autos/hora. ¿Cuál es la probabilidad de que lleguen 3 autos entre las 5 y las 6, dado que llegaron 2 autos entre las 3 y las 4? Incrementos Estacionarios: La probabilidad de ocurrencia de eventos en un intervalo de tiempo depende sólo del tamaño del intervalo. Ej: La llegada de autos a un estacionamiento se puede representar como un Proceso de Poisson de tasa λ autos/hora . ¿Cuál es la probabilidad de que lleguen 5 autos entre las 6 y las 8? Procesos de Poisson Tiempos Entre llegadas Distribución Exponencial: Distribución Exponencial: Tiempos Entre llegadas Tiempo que transcurre hasta la k-ésima llegada en un Proceso de Poisson Tiempo que transcurre hasta la k-ésima llegada en un Proceso de Poisson Modelación de las llegadas (Procesos de Poisson) Profesor: Yerko Sánchez Simulación de Sistemas