Informe de Laboratorio: Movimiento Periódico y Constantes Físicas
Anuncio

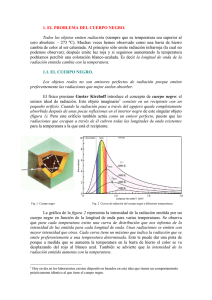
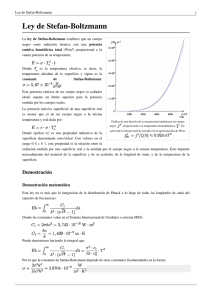
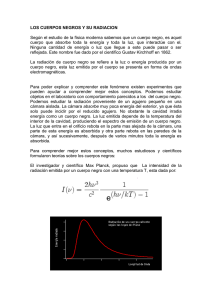
Estudio del movimiento periódico del sistema masa-resorte Jehison Manquillo – Wiler Morán – Esneider Lugo Grupo 05 Departamento de Física, Universidad del Valle, Cali, Colombia (Fecha: 17 de Noviembre del 2020) En esta práctica de laboratorio vamos a medir la constante de un constante de StefanBoltzmann y la constante de desplazamiento de Wien por medio de un programa de internet, en el cual se debe medir para una temperatura dada la energía, longitud de onda. Estos datos hay que consignarlas una tabla, para que así con la ayuda de estas y de algunas ecuaciones podamos sacar el resultado de las constantes. Procedimiento: La información que obtenemos es que para la temperatura de 200K de un cuerpo negro (tierra) la longitud de onda de máxima emisión se da en el infrarrojo, con un valor de 14.489 μm=14.489 x10 -6 m (ver el valor en el eje horizontal de la gráfica) y la intensidad, que es la energía de radiación total emitida en unidad de área en unidad de tiempo E tiene un valor de 9.07x10 1 W/m 2 (ver el valor en el recuadro del lado derecho). Luego, se sigue variando la temperatura acomodando las escalas vertical y horizontal para poder visualizar bien la gráfica anotando cada vez los valores de λ y E. Hacerlo para 22 valores de temperatura. Figura 1: Toma de datos de laboratorio Después de tomar todos lo 22 datos se insertan los datos en la siguiente tabla, T(K) E (W/m2) 200 90,1 550 5190 900 37200 1250 138000 1600 372000 1950 820000 2300 1590000 2650 3000 3350 3700 4050 4400 4750 λ (m) T4 0,00001448 1600000000 9 0,00000526 9150625000 9 0 1/T 0,005 0,0018181 82 0,0011111 11 0,00000322 6,561E+11 0,00000231 8 0,00000181 1 0,00000148 6 2,44141E+1 2 0,0008 6,5536E+12 0,000625 0,00000126 0,00000109 3 0,00000096 4590000 6 0,00000086 7140000 5 0,00000078 10600000 3 0,00000071 15300000 5 0,00000065 21300000 9 2800000 28900000 0,00000061 1,4459E+13 2,79841E+1 3 4,93155E+1 3 8,1E+13 1,25945E+1 4 1,87416E+1 4 2,69042E+1 4 3,7481E+14 5,09066E+1 4 0,0005128 21 0,0004347 83 0,0003773 58 0,0003333 33 0,0002985 07 0,0002702 7 0,0002469 14 0,0002272 73 0,0002105 26 5100 5450 38400000 0,00000056 8 0,00000053 50000000 2 5800 64200000 6150 81100000 6500 6850 7200 7550 10100000 0 12500000 0 15200000 0 19400000 0 0,0000005 0,00000047 1 0,00000044 6 0,00000042 3 0,00000040 2 0,00000037 9 6,7652E+14 8,82239E+1 4 1,13165E+1 5 1,43054E+1 5 1,78506E+1 5 2,20172E+1 5 2,68739E+1 5 3,24929E+1 5 0,0001960 78 0,0001834 86 0,0001724 14 0,0001626 02 0,0001538 46 0,0001459 85 0,0001388 89 0,0001324 5 Tabla 1: Datos obtenidos La ley de Stefan-Boltzmann indica que la energía de radiación total emitida desde el cuerpo negro es proporcional a la cuarta potencia de su temperatura absoluta, esto es: Dónde: E es la energía emitida por el cuerpo negro a una temperatura T y σ es una constante de proporcionalidad llamada constante de Stefan -Boltzmann y tiene un valor de 5.670367 × 10−8 W.m−2 ⋅K −4 . De los datos obtenidos podemos deducir el valor de la constante de Stefan-Boltzmann graficando E vs T4, lo que nos da así: Figura 2: Grafica energía vs Temperatura a la 4 Dando como resultado para la constante de Stefan-Boltzmann 5.79x10-8 W.m−2 ⋅K −4 . La ley de desplazamiento de Wien dice que el espectro de radiación del cuerpo negro a cualquier temperatura se relaciona con el espectro a cualquier otra temperatura. De esto, se deduce que la longitud de onda de máxima emisión es una función que depende únicamente de la temperatura, esto es: Dónde: λ es la longitud de onda y la parte derecha del igual es la constante de desplazamiento de Wien cuyo valor más exacto es de 2.8977729 × 10 −3 K .m . De la tabla podemos graficar la λ vs 1/T, que, al trazar una línea de tendencia, la pendiente de la ecuación nos dará el valor de la constante de Wien. Así: Figura 3: Grafica longitud de onda vs inverso de la temperatura Dando como resultado para la constante de desplazamiento de Wien 2.9x10 -3. Discusión Para la constante de Stefan-Boltzmann se encontró un valor experimental de 5.79x10 -8 W.m−2 ⋅K −4 comparado con el valor teórico real que es de 5.670367 × 10 −8 W.m−2 ⋅K −4 da un error en la medición de 2.1%, error probablemente producido por la toma de los valores de las energías, pues estas solo se tomaban con tres cifras significativas en notación científica para cada temperatura. En la constante de desplazamiento de Wien se encontró un valor experimental de 2.9x10-3 K .m que comparado con el valor que tiene la está de 2.8977729 × 10 −3 K .m, da un error en la medición de 3,37%, lo cual es un error admisible. Conclusión En la práctica realizada se ha comprobado la ley de Stefan -Boltzmann de la radiación de un cuerpo negro. Se ha comprobado que la potencia emitida por un cuerpo negro es proporcional a la cuarta potencia de su temperatura absoluta y se ha podido determinar que la constante de proporcionalidad es la constante de Stefan -Boltzmann, Hay que recordar las condiciones físicas en las que se puede aplicar el modelo de cuerpo negro: la radiación tiene que ser testigo del equilibrio térmico del objeto considerado. Sin esta hipótesis, la aplicación de las leyes anteriores no puede ser utilizada y puede llevar a malas interpretaciones. En primera aproximación, las estrellas radian como cuerpos negros, pero las numerosas líneas de absorción pueden deformar el aspecto de distribución de la radiación. La radiación del fondo cosmológico es un excelente cuerpo negro.