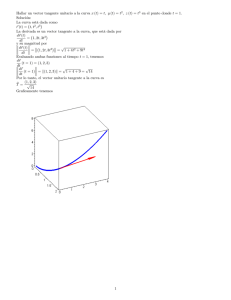
Tema 3
Cálculo diferencial de varias
variables
3.1.
INTRODUCCIÓN
En este tema haremos una breve incursión en el cálculo diferencial para funciones de varias variables, con el objetivo de adquirir los conceptos necesarios para desarrollar una teoría de optimización
para tales funciones. Debemos ser conscientes de que la mayoría de los problemas que aparecen en la
práctica tratan con funciones de más de una variable. Por ejemplo, el volumen de un cilindro circular,
V = πr2 h, es una función con dos variables: el radio r de la base y la altura h. El volumen de un sólido
rectangular, V = anchura × profundidad × altura, es una función de tres variables. La presión de un
gas depende del volumen y de la temperatura, luego es una función de dos variables. La temperatura
en una localidad puede depender de variables como la altura, el número de días de Sol al año, el tipo
de vegetación circundante, la cercanía a una gran masa de agua, la pluviometría, etc. En el ámbito
económico, podemos encontrarnos con numerosas funciones de varias variables, desde el crédito para
una hipoteca, que depende del interés y del número de años, hasta la función de beneficios de una
empresa que puede depender de argumentos tales como el número de trabajadores empleados, el número de horas de trabajo, las inversiones en tecnología o publicidad, o la renta de los clientes. Esta
función de beneficios es, pues, una función de varias variables. En general, los modelos matemáticos
serán más fiables y más ajustados a la realidad cuanto mayor número de variables tengan en cuenta.
Como contrapartida, su estudio puede resultar más complicado.
Vamos pues a estudiar funciones f : X → Y con X ⊆ Rn e Y ⊆ R, de modo que lo dicho en el
tema anterior corresponde al caso n = 1; ahora trataremos preferentemente los casos n = 2, 3.
3.1.1.
Funciones de varias variables
Para n ≥ 2, los dominios de las funciones
f : D ⊂ Rn −→
(x1 , x2 , . . . , xn ) 7−→
R
f (x1 , x2 , . . . , xn ).
que usaremos tienen una variedad mayor de formas que en una variable, lo que exige conocer algo
sobre los subconjuntos de Rn de uso más habitual.
Algunas regiones del plano
Usualmente, las curvas dividen al plano en regiones, como, por ejemplo:
• Semiplano. Una recta y = ax + b divide un plano en dos semiplanos: y ≤ ax + b e y ≥ ax + b. La
intersección de semiplanos puede dar lugar a regiones angulares o a bandas. En la figura siguiente se
pueden ver representados el semiplano y ≤ 2x + 1 (izquierda), y la banda 2 ≤ x ≤ 4 (derecha), que a
su vez está formada por la intersección de los semiplanos x ≥ 2 y x ≤ 4.
1
3
3
2
2
1
1
-1.0
-0.5
0.5
1.0
1.5
2.0
-1
-1
1
2
3
4
5
-1
• Región elíptica. Una elipse centrada en un punto (h, k) con semieje horizontal a y semieje vertical
b está formada por los puntos del plano que cumplen la ecuación situada abajo a la izquierda. La elipse
divide el plano en dos regiones, la interna verifica la desigualdad situada abajo a la derecha.
(y − k)2
(x − h)2
+
= 1,
2
a
b2
(h,k)
(x − h)2
(y − k)2
+
≤ 1.
2
a
b2
b
(h,k)
b
a
a
Ejemplos. Representa gráficamente las regiones dadas por dos condiciones: (a) −1 ≤
(b) y ≥ x, x2 − 2x + y 2 ≤ 0.
2x−y+2
3
≤ 1.
• Círculo. Un caso particular de la región elíptica es el círculo, que se presenta cuando los semiejes
son iguales, dando lugar al segmento llamado radio. Entonces, la elipse se convierte en circunferencia.
Dicho de otra forma, una circunferencia centrada en el punto (h, k) y de radio r está formada por los
puntos (x, y) que satisfacen la ecuación: (x − h)2 + (y − k)2 = r2 . El círculo centrado en (h, k) y de
radio r está formado por los puntos que satisfacen (x − h)2 + (y − k)2 ≤ r2 .
r
r
(h,k)
r
(h,k)
r
Con el lenguaje
p de los vectores, se llama norma del vector ~v = (x, y) al número real positivo
x2 + y 2 que determina la longitud del vector, o sea, la distancia desde el punto
o nulo k~v k =
extremo del vector al origen. Análogamente, dados dos puntos C(h, k) y P (x, y), se tiene el vector
P − C = (x − h, y − k), de modo que la ecuación de la circunferencia se puede escribir de esta manera:
{P ∈ R2 | kP − Ck2 = r2 }. Con esta notación vectorial podemos considerar la figura análoga del
círculo en dimensión
p n cualquiera. Por ejemplo, si ~v = (x, y, z) es un vector del espacio, su norma o
longitud es k~v k = x2 + y 2 + z 2 y la distancia entre dos puntos C(h, k, l) y P (x, y, z) es la norma del
vector P − C = (x − h, y − k, z − l), de modo que la ecuación de la esfera de centro C y radio r es
{P ∈ R3 | kP − Ck2 = r2 }.
Bolas abiertas y conjuntos abiertos
p
Ahora consideramos vectores ~x = (x1 , . . . , xn ) ∈ Rn con la norma k~xk = x21 + · · · + x2n . La
distancia entre dos puntos x = (x1 , . . . , xn ) y a = (a1 , . . . , an ) es la norma del vector x − a =
(x1 − a1 , . . . , xn − an ), de modo que la ecuación de la «esfera» de Rn con centro a y radio r es
{x ∈ Rn | kx − ak2 = r2 }. En relación con las «esferas» de Rn se pueden introducir nomenclaturas
útiles para el estudio de los subconjuntos relacionados con las funciones de n variables.
2
Definición 1. Sea a ∈ Rn y r ∈ R positivo. Llamamos n-bola abierta de centro a y radio r al
conjunto de puntos de Rn cuya distancia al punto a es menor que r, es decir:
B(a, r) := {x ∈ Rn | kx − ak < r}.
Los casos particulares que más usaremos son:
En R se trata de intervalos abiertos centrados en a: B(a, r) = (a − r, a + r).
En R2 son los círculos excluyendo los puntos de la circunferencia.
En R3 son los puntos de la región esférica limitada por la esfera excluyendo los puntos de esta.
Definición 2 (Punto interior y conjunto abierto). Sea S ⊂ Rn y a ∈ S. Se dice que a es un punto
interior de S si existe r > 0 tal que B(a, r) ⊂ S. El conjunto de todos los puntos interiores de S
se llama interior de S y se denota Int S. Un conjunto S ⊂ Rn es abierto si todos sus puntos son
interiores, es decir: S = Int S.
S
a
Int S
Definición 3 (Exterior y frontera). Un punto x ∈ Rn se llama exterior al conjunto S ⊂ Rn si existe
una n-bola abierta centrada en x que no contiene puntos de S, es decir, si es interior al conjunto
complementario Rn \ S. El conjunto de todos los puntos exteriores a S se llama conjunto exterior de
S y se denota por Ext S. Un punto que no es exterior ni interior se llama punto frontera. El conjunto
de todos los puntos frontera de S se llama frontera de S y se denota ∂S.
Ext S
a
S
¶S
a
S
Ejemplo. Sea S = {(x, y) ∈ R2 | x2 + y 2 ≤ 1}. Representar y dar las ecuaciones de Int S, Ext S y ∂S.
Gráficas
La gráfica de una función f : X → Y real de n variables está formada por todos los puntos
(x, f (x)) ∈ Rn+1 con x ∈ X. Al estudiar funciones de varias variables, se pierde en ocasiones la
componente visual y geométrica que tiene el estudio de funciones de una variable, cuyas gráficas se
representan en el plano. Para que la podamos representar gráficamente ha de ser n ≤ 2. El caso n = 1
ya es conocido y en el caso de funciones de dos variables se mantiene esta peculiaridad con gráficas
definidas en el espacio tridimensional. En este caso, la gráfica de f es el conjunto de puntos (x, y, z)
que satisfacen z = f (x, y) con (x, y) en el dominio de f .
En la figura siguientepse muestra el esquema general junto con el ejemplo de la semiesfera dada
por la función f (x, y) = 25 − x2 − y 2 cuyo dominio es el círculo centrado en (0, 0) y de radio 5. Su
recorrido o conjunto imagen es el intervalo [0, 5].
3
4
Hx,y,f Hx,yLL
Z
5
2
0
Hx,y,0L
0
-5
Y
0
X
-5
5
Ejemplos. Los ejemplos siguientes con dominio R2 tienen su representación gráfica debajo:
2
2
(a) f (x, y) = y + sen x. (b) f (x, y) = e−(x +y ) .
5
Y
0
-5
5
isobaras o en las lı́neas isotermas de los mapas meteorológicos (figura 4) o en las curvas
de nivel de los mapas topográficos (figura 5).
En un mapa de contorno se muestra la variación de z respecto a x e y medianisobaras
o en de
las nivel.
lı́neas Una
isotermas
de los grande
mapas meteorológicos
(figura
4) o indica
en las curvas
te
las curvas
separación
entre las curvas
de nivel
que z
de nivel
de loslentamente,
mapas topográficos
5). de nivel muy próximas indican que z
está
variando
mientras(figura
que curvas
Otra
forma
de
visualizar
la
gráfica
de
una
función
= f (x,de
y) zesrespecto
mediantecuando
nivel
de
En
un
mapa
de
contorno
se
muestra
la
acurvas
x e yde
está variando muy deprisa. Por ejemplo, en variación
un zmapa
cartográfico,
lasmedianlı́neas
ecuación
f
(x,
y)
=
k,
siendo
k
una
constante
que
indica
la
altura
a
la
que
se
hace
una
sección
te nivel
las curvas
nivel.
Unaquiere
separación
grande
entre del
las terreno
curvas de
nivel muy
indica
que z
de
están de
muy
juntas
decir que
la altura
cambia
bruscahorizontal de la gráfica. En un mapa de curvas de nivel es importante elegir alturas k espaciadas de
está variando
lentamente,
mientrasante
que algún
curvasaccidente
de nivel geográfico
muy próximas
indican
que z
mente,
por lo que
nos encontramos
del tipo
barranco,
manera uniforme. Esta representación es familar, ya que aparecen en las líneas isobaras o en las líneas
está
variando
muy
deprisa.
Por
ejemplo,
en
un
mapa
cartográfico,
cuando
las
lı́neas
acantilado,
cortado,
ladera
de
una
montaña,
etc.
isotermas de los mapas meteorológicos o en las curvas de nivel de los mapas topográficos.
de Una
nivel
están muy
juntas
decir
la que
altura
del
terreno
cambia
muy mientras
bruscaseparación
grande
entre quiere
curvas de
nivelque
indica
z está
variando
muy
lentamente,
que
curvas
de
nivel
muy
próximas
indican
que
z
está
variando
muy
deprisa.
Por
ejemplo,
en
un
mapa
mente, por lo que nos encontramos ante algún accidente geográfico del tipo barranco,
cartográfico,
que
las
líneas
de
nivel
estén
muy
juntas
quiere
decir
que
la
altura
del
terreno
cambia
acantilado, cortado, ladera de una montaña, etc.
Z
2
1.0
0
Z
-5
0.5
1
0.0
-2
0
Y
-1
-5
-1
0
X
0
1
X
5
2
-2
muy bruscamente, por lo que nos encontramos ante algún barranco, acantilado, etc.
Figura 4: Lı́neas de presión constante (isobaras) y de temperatura constante (isotermas)
en los mapas del tiempo.
Líneas isobaras e isotermas en los mapas del tiempo
Figura 4: Lı́neas de presión constante (isobaras) y de temperatura constante (isotermas)
en los mapas del tiempo.
Curvas de nivel en mapas topográficos.
Figura 5: Curvas de nivel en mapas topográficos.
En las gráficas de la figura 6 se muestra una superficie y su correspondiente mapa
de contorno, en el que
se aprecian
lasde
variaciones
de la función
z. Se aprecian en blanco
Figura
5: Curvas
nivel en mapas
topográficos.
4
las zonas ((más altas)) y en negro las ((más profundas)).
En las gráficas de la figura 6 se muestra una superficie y su correspondiente mapa
de contorno, en el que se aprecian las variaciones de la función z. Se aprecian en blanco
3.2.
3.2.1.
CÁLCULO DIFERENCIAL
Derivadas parciales
Veamos cómo extender el concepto de derivabilidad a funciones de varias variables. En este curso
sólo haremos un acercamiento a este concepto. No obstante, el estudio general puede encontrarse
en cualquier libro que trate el cálculo diferencial en varias variables. Por simplicidad, empezamos
estudiando el caso de dos variables.
Definición 4. Sea f : U ⊂ R2 −→ R una función definida en un abierto U de R2 y P = (a, b) un
punto de U . La derivada parcial de f respecto a x en el punto P es
f (a + h, b) − f (a, b)
∂f
(P ) = lı́m
h→0
∂x
h
si este límite existe y es un número real. Otras notaciones habituales para esta derivada parcial son
fx (P ), f1 (P ), o D1 f (P ). Análogamente, la derivada parcial de f respecto a y en el punto P es
fy (P ) = f2 (P ) = D2 f (P ) =
∂f
f (a, b + h) − f (a, b)
(P ) = lı́m
.
h→0
∂y
h
Notemos que la derivada parcial respecto a x (respectivamente, y) es como la derivada en una
variable suponiendo que la variable y (respectivamente, x) es una constante. En fx , el incremento de
la variable dependiente se produce al desplazarnos del punto (a, b) sólo en la dirección del eje X. Así,
si dejamos fija b, nos queda la función de una variable ϕ(x) = f (x, b), con lo cual ϕ0 (a) = ∂f
∂x (a, b). La
gráfica de f (x, y) es una superficie. La derivada parcial fx (a, b) es la pendiente de dicha superficie en
el punto (a, b, f (a, b)) cuando nos desplazamos en la dirección del eje X, es decir, de la tangente a la
curva intersección de la superficie con el plano de ecuación y = b. Análogo para fy (a, b).
Y
X
f Ha,bL-f Ha+h,bL
f Ha,bL-f Ha+h,bL
Z
h
Ha,b,0LHa+h,b,0L
h
Z
Ha,b,0L
Ha+h,b,0L
X
Y
Ejemplo. Sea f (x, y) = x2 + y 2 sen(xy). Calcular las derivadas parciales fx y fy . Calcular fx (0, 0).
Derivando, si se puede, una derivada parcial se van obteniendo las derivadas de orden dos:
∂2f
∂f ∂f
∂2f
∂f ∂f
∂2f
∂f ∂f
∂2f
∂f ∂f
.
=
,
=
,
=
,
=
∂x ∂x
∂x2
∂x ∂y
∂x ∂y
∂y ∂x
∂y ∂x
∂y ∂y
∂2y
Con otra notación (fx )x = fxx , (fx )y = fxy , (fy )x = fyx , (fy )y = fyy . Derivando, cuando se pueda,
una derivada de orden dos obtenemos las derivadas de orden 3 y así sucesivamente.
Ejemplo. Sea f (x, y) = x2 + y 2 sen(xy). Calcular las derivadas parciales de segundo orden.
Se puede observar en el ejemplo anterior que las derivadas parciales cruzadas fxy , fyx coinciden.
¿Ha sido casualidad o es algo habitual? El siguiente resultado nos dice que esto ocurre en muchas
ocasiones.
Teorema 1 (de Schwarz). Sea f : U ⊂ R2 −→ R, U abierto. Si las derivadas
y
2
∂ f
∂y ∂x
∂2f
∂x ∂y
: U ⊂ Rn −→ R
: U ⊂ Rn −→ R existen y son continuas en U , entonces
∂2f
∂2f
=
.
∂x ∂y
∂y ∂x
Definición 5. Sea U ⊂ R2 abierto y f : U ⊂ R2 −→ R. Diremos que f ∈ C 2 (U ) si posee todas las
derivadas parciales de orden dos (fxx , fxy , fyx , fyy ) y son funciones continuas en U .
5
Plano tangente
Cuando tenemos una función f : U ⊂ R2 −→ R, a menudo escribimos z = f (x, y). Esto representa
una superficie en el espacio.
Dado un punto (a, b) ∈ U , y supuesto que f tiene derivadas parciales fx y fy continuas, el plano
tangente en el punto (a, b, f (a, b)) ∈ R3 es
z = f (a, b) + fx (a, b)(x − a) + fy (a, b)(y − b).
Gradiente y hessiana con n variables
Si una función z = f (x1 , x2 , . . . , xn ) tiene más de dos variables, las derivadas parciales fx1 , fx2 ,
. . . , fxn se definen de modo análogo. Todos los resultados vistos con n = 2 son válidos para funciones
de un número n arbitrario de variables. Una función de n variables suficientemente derivable tiene
n derivadas parciales de primer orden, n2 de segundo orden, etc., que se pueden disponer en forma
vectorial o matricial.
Definición 6. Sea f : D ⊂ Rn −→ R. En los puntos donde las derivadas parciales existan, llamamos:
• Gradiente de f al vector
∂f
∂f
,...,
∈ Rn .
grad f = ∇f =
∂x1
∂xn
Cuando convenga considerar a este vector como una matriz
o jacobiana, escribiendo f 0 = (fx1 , . . . , fxn ).
• Matriz hessiana de f a la matriz n × n
fx1 x1 fx1 x2 . . .
fx2 x1 fx2 x2 . . .
Hf =
...
...
...
fxn x1 fxn x2 . . .
1 × n, la denominaremos matriz derivada
f x1 xn
f x2 xn
.
...
f xn xn
Nota. Si f ∈ C 2 (U ), como consecuencia del teorema de Schwartz, la matriz hessiana será simétrica.
Unas funciones de n variables muy particulares son las n proyecciones pri : Rn → R, 1 ≤ i ≤ n,
definidas por pri (x1 , . . . , xn ) = xi . Su gradiente es el vector coordenado correspondiente, ∇ pri = e~i ,
y la matriz hessiana es nula.
3.2.2.
Derivación de funciones generales
Las funciones reales en general son de la forma F : X → Y con X ⊆ Rn e Y ⊆ Rm . Componiendo
con las proyecciones tenemos m funciones componentes de n variables, a saber fi = pri ◦F , 1 ≤ i ≤ m,
así que escribimos la función en la forma F = (f1 , . . . , fm ):
F (x1 , . . . , xn ) = (f1 (x1 , . . . , xn ), . . . , fm (x1 , . . . , xn )).
Si todas las derivadas parciales existen, tendremos un total de mn, pues cada una de las m
funciones fi se pueden derivar respecto a sus n variables. Obtendremos por tanto una matriz m × n
de derivadas parciales que se llama la matriz derivada o jacobiana de F , cuyas filas son los gradientes
de las funciones componentes. Es decir:
f1x1 f1x2 . . . f1xn
∂(f1 , . . . , fm )
f2x1 f2x2 . . . f2xn
=
F0 =
... ...
...
∂(x1 , . . . , xn ) . . .
fmx1 fmx2 . . . fmxn
Estas funciones generales y sus derivadas tienen interpretación geométrica, en varios casos de sumo
interés.
6
Curvas paramétricas
Pensemos en las ecuaciones de movimiento de una partícula que se desplaza por el plano. En cada
momento, la partícula estará en un punto de coordenadas (x, y). Pero como la partícula se mueve, su
posición variará en función del tiempo, es decir, sus coordenadas son funciones del tiempo (x(t), y(t)).
A este tipo de ecuaciones se les llama paramétricas, porque la posición de la partícula depende de un
parámetro: el tiempo.
Ejemplo. Una partícula se desplaza por el plano según su ecuación paramétrica (x, y) = (0, 1) +
t(−2, 1), t ∈ R, donde t representa el tiempo. Otra partícula sigue la ecuación (x, y) = (2, 0) + t(−4, 2),
t ∈ R. ¿Tienen la misma trayectoria? Para t = 0, ¿están en el mismo punto? ¿van a la misma velocidad?
Pero también se pueden expresar las curvas en función de otros parámetros diferentes del tiempo,
aunque ellos a su vez dependan del tiempo en su variación. Las ecuaciones paramétricas son un modo
de representar curvas.
Definición 7. Una curva paramétrica en Rn es una función α : D ⊆ R → Rn , α(t) = (α1 (t), . . . , αn (t)),
cuyas funciones componentes αi (t) de una variable se pueden derivar al menos dos veces.
En general, el dominio de una curva paramétrica será un intervalo cerrado [a, b] de R y la curva se
expresa mediante sus llamadas ecuaciones paramétricas:
x1 = α1 (t),
α : ...
a ≤ t ≤ b,
xn = αn (t),
en las que t es un parámetro arbitrario, no necesariamente interpretable como tiempo.
La curva geométrica es la imagen de la curva paramétrica. Esta da más información que sólo la
curva geométrica, pues también indica un modo de recorrerla. Una misma curva puede tener parametrizaciones diferentes (recordar el ejemplo anterior); por ejemplo, hay muchos modos en los que una
partícula puede recorrer la misma trayectoria.
La matriz derivada de α es la matriz columna
0 0
x1
α1
α0 = . . . = . . . .
x0n
αn0
~0 (t) que
Al ser una matriz columna puede también ser interpretada como un vector variable α
admite dos interpretaciones:
~0 (t) es el vector direccional de la tangente a la curva paramétrica en el punto α(t).
Geométrica: α
La ecuación vectorial de la tangente en el punto α(a) correspondiente a un valor fijo t = a del
~0 (a), λ ∈ R. Tomando
parámetro será por tanto, con x = (x1 , . . . , xn ) ∈ Rn : x = α(a) + λα
componentes, se escribe en forma paramétrica como
0
x1 = α1 (a) + λα1 (a),
λ ∈ R.
...
0
xn = αn (a) + λαn (a),
~0 (t) es el vector velocidad instantánea que corrresponde
Cinemática: Cuando t es el tiempo, α
al recorrido de la curva determinado por la parametrización, que indica una dirección y tie~0 (t)k. Además, el vector derivada segunda α~00 (t) se interpreta como la
ne un valor absoluto kα
aceleración.
Curvas implícitas
Trataremos únicamente el caso plano. Es bien sabido que cada recta del plano tienen una ecuación
implícita ax + by + c = 0, que corresponde a los puntos en los que se anula la función f : R2 → R
del primer miembro f (x, y) = ax + by + c. A su vez, tiene una ecuación paramétrica como rectas que
pasan por un punto (p, q) y tiene un determinado vector direccional w(u,
~
v):
(
x = p + tu,
α:
t ∈ R,
y = q + tv,
7
Se trata de la misma recta si f ◦ α es la función constante en 0, lo que se traduce en dos ecuaciones
ap + bq + c = 0, au + bv = 0 que indican, respectivamente, que el punto (p, q) verifica la ecuación
implícita y que el vector w
~ verifica la ecuación implícita homogénea o, en términos de vectores, que el
vector w
~ es perpendicular al vector (a, b); se dice por ellos que (a, b) es un vector normal a la recta.
Se plantea una situación similar con las curvas generales del plano.
Dada una función f : X ⊆ R2 → R con 0 en su imagen, el subconjunto f −1 (0) = {(x, y) ∈
X | f (x, y) = 0} es una curva plana dada por una ecuación implícita f (x, y) = 0. Entonces, una
curva paramétrica α : I ⊆ R → R2 es una representación de la curva f (x, y) = 0 si α(I) ⊆ X y la
composición f ◦ α : I → R es la función constante nula, es decir, f (x(t), y(t)) = 0 para cada t ∈ I.
Un ejemplo elemental es la circunferencia de ecuación implícita x2 + y 2 = a2 , que es de la forma
−1
f (0) para la función f (x, y) = x2 + y 2 − a2 . La circunferencia tiene la representación paramétrica
(
x = a cos t,
t∈R
α:
y = a sen t,
que es una función α : I ⊆ R → R2 cuyo dominio puede ser [0, 2π] o bien todo R. Se tiene, en efecto,
(a cos t)2 + (a sen t)2 − a2 = 0.
Superficies paramétricas
Podemos pensar que una superficie está formada por las posibles posiciones en el espacio de una
partícula que puede moverse dependiendo de dos parámetros.
Definición 8. Una superficie paramétrica en Rn es una función S : D ⊆ R2 → Rn , S(u, v) =
(f1 (u, v), . . . , fn (u, v)), cuyas funciones componentes fi (u, v) de dos variables se pueden derivar al
menos dos veces.
Por razones prácticas, trataremos únicamente superficies en R3 . La superficie se describe mediante
sus llamadas ecuaciones paramétricas:
x = x(u, v),
(u, v) ∈ D.
S : y = y(u, v),
z = x(u, v),
La superficie geométrica (subconjunto de R3 ) es la imagen de la superficie paramétrica. Ésta da
más información que sólo la superficie geométrica, pues también indica un modo de recorrerla. Una
misma superficie puede tener parametrizaciones diferentes.
La matriz derivada de S es la matriz 3 × 2
xu
S 0 = yu
zu
xv
yv .
zv
Esta matriz puede verse como un par de vectores variables de compomentes sus columnas S~u (u, v),
S~v (u, v) que admiten esta interpretación geométrica siempre que estos vectores sean independientes
(es decir, sea 2 el rango de la matriz derivada S 0 ): Fijemos un punto (u, v) = (a, b) ∈ D del dominio
de S. Entonces S(u, b) es una curva paramétrica de parámetro u que está contenida en la superficie
y pasa por el punto S(a, v). El vector direccional de la tangente en u = a a esta curva es S~u (a, b).
Análogamente: S(a, b) es una curva paramétrica de parámetro v que está contenida en la superficie y
pasa por el punto S(a, b). El vector direccional de la tangente a esta curva en v = b es S~v (a, b).
La ecuación vectorial del plano tangente en el punto S(a, b) será, por tanto, con (X, Y, Z) =
S(a, b) + λS~u (a, b) + µS~v (a, b), (λ, µ) ∈ R2 , que tomando componentes se escribe en forma paramétrica
como
X = x(a, b) + λxu (a, b) + µxv (a, b),
(λ, µ) ∈ R2 .
Y = y(a, b) + λyu (a, b) + µyv (a, b),
Z = z(a, b) + λzu (a, b) + µzv (a, b),
8
Superficies implícitas
Es bien sabido que cada plano del espacio tridimensional tiene una ecuación implícita ax + by +
cz + d = 0, que corresponde a los puntos en los que se anula la función f : R3 → R del primer miembro
f (x, y, z) = ax + by + cz + d. A su vez, tiene una ecuación paramétrica como plano que pasa por un
punto y tiene dos vectores independientes que marcan su subespacio de vectores direccionales:
0
x = p + λu + µu ,
S : y = q + λv + µv 0 ,
λ, µ ∈ R.
0
z = r + λw + µw ,
Se trata del misma plano si f ◦ S es la función constante en 0, lo que se traduce en tres ecuaciones
ap+bq +cr = 0, au+bv +cw = 0, au0 +bv 0 +cw0 = 0 que indican, respectivamente, que el punto (p, q, r)
verifica la ecuación implícita y que los vectores (u, v, w) y (u0 , v 0 , w0 ) verifican la ecuación implícita
homogénea (sin término independiente) del plano, lo que significa que ambos son perpendiculares al
vector (a, b, c), que es por tanto un vector normal al plano.
Ejemplo. Dar la ecuación del plano que pasa por (2, 1, 3) y tiene a η = (2, −4, 5) como vector perpendicular. Dar también una ecuación paramétrica del plano.
Se plantea una situación similiar con todas las superficies del espacio tridimensional. Dada una
función f : X ⊆ R3 → R con 0 en su imagen, el subconjunto f −1 (0) = {(x, y, z) ∈ X | f (x, y, z) = 0}
es una superficie en el espacio dada por una ecuación implícita f (x, y, z) = 0. Entonces, una superficie
paramétrica S : D ⊆ R2 → R3 es una representación de la superficie f (x, y, z) = 0 si S(D) ⊆ X y la
composición f ◦ S : D → R es la función constante nula, es decir, f (x(u, v), y(u, v), z(u, v)) = 0.
f
Un ejemplo elemental es la esfera de ecuación implícita x2 + y 2 + z 2 = a2 , que es de la forma
(0) para la función f (x, y) = x2 + y 2 + z 2 − a2 . La esfera tiene la representación paramétrica
x = a cos u sen v,
u ∈ [0, 2π], v ∈ [0, π],
S : y = a sen u sen v,
z = a cos v,
−1
que es una función S : D ⊆ R2 → R3 cuyo dominio es D = [0, 2π] × [0, π] ∈ R2 . Se tiene, en efecto,
(a cos u sen v)2 + (a sen u sen v)2 + (a cos v)2 − a2 = 0.
2
2
2
La generalización natural de la esfera es el elipsoide de semiejes a, b, c y ecuación xa2 + yb2 + zc2 = 1.
1.0
Y
0.5
0.0
-0.5
2
-1.0
1.0
0.5
Z
Z
0
0.0
2
-0.5
1
-2
-1.0
-1.0
0
-0.5
Y
0.0
-1
-1
X
0.5
0
1
X
1.0
Otras superficies notables son el paraboloide elíptico z =
x2
a2
+
y2
b2
y el cono elíptico z =
4
Y
2
0
-2
4
Y
-4
4
2
0
-2
-4
3
Z
2.0
1.5
2
Z 1.0
1
0.5
0.0
0
-2
-2
-1
0
X
-1
0
1
X
2
9
1
-2
2
q
x2
a2
+
y2
b2 .
3.2.3.
Regla de la cadena
La regla de la cadena explica el método de derivación de una función que es la composición de
otras dos funciones. Recordemos la regla de la cadena dada para funciones reales de una variable: Si
f (x) es derivable en x0 y g(x) es derivable en f (x0 ), entonces (g ◦ f )(x) es derivable en x0 y se verifica
(g ◦ f )0 (x0 ) = g 0 (f (x0 )) · f 0 (x0 ).
Si nos referimos a funciones reales generales, la regla se conserva con su misma expresión, si f 0 , g 0
son las matrices derivadas de f, g, respectivamente, y los puntos se refieren al Rn que corresponda.
Veamos ejemplos genéricos a partir de una función de n variables f : X ⊆ Rn → Y ⊆ R. Hay dos
tipos de composiciones posibles, o bien f ◦ g o bien α ◦ f .
g
f
α
D ⊆ Rp −
→ X ⊆ Rn −
→Y −
→ Rm .
Las variables que usaremos son (u1 , . . . , up ) ∈ D, (x1 , . . . , xn ) ∈ X, (y1 , . . . , ym ) ∈ Rm . Las matrices
derivadas de cada una de las funciones mencionadas son
0
g1u1 g1u2 . . . g1up
y1
g2u1 g2u2 . . . g2up
..
0
0
0
g = .
..
..
.. , f = (fx1 , . . . , fx1 ), α = . ,
..
.
.
.
yn0
gnu1 gnu2 . . . gnup
(f ◦ g)0 = (fx1 , . . . , fx1 )
g1u1
g2u1
..
.
g1u2
g2u2
..
.
...
...
..
.
g1up
g2up
..
.
gnu1
gnu2
...
gnup
,
y10
(α ◦ f )0 = ... (fx1 , . . . , fx1 ).
yn0
Pasamos ahora a desarrollar algunos ejemplos particulares con valores pequeños de p, n, m y usando
letras diferentes para las componentes en vez de subíndices, como suele hacerse en la práctica. Usaremos
también la notación de Leibniz.
α
f
• Caso D ⊆ R −
→ X ⊆ R2 −
→ Y ⊆ R. Tenemos la función f de dos variables, que podemos
expresar de la forma z = f (x, y), o también z = z(x, y). Además, en el dominio plano de f tenemos
una curva α cuyas ecuaciones son (x, y) = (x(t), y(t)). Componiendo resulta una función de una
variable z = z(t) = z(x(t), y(t)). Si todas las funciones son derivables se tiene
0 x
0
0
z = z (t) = (zx , zy )
= zx x0 + zy y 0 .
y0
Lo podemos expresar con la notación de Leibniz:
∂z ∂z
∂z dx ∂z dy
dz
dx/dt
0
=
,
=
+
.
z =
dy/dt
dt
∂x ∂y
∂x dt
∂y dt
Veamos por último la interpretación geométrica. La gráfica de f es una superficie S con parámetros
x, y, mientras que la curva plana α se completa con z = f (x, y) para ser una curva β sobre la
superficie S:
x = x
x = x(t)
β : y = y(t) ⊂ S : y = y
.
z = z(t)
z = z(x, y)
En cada punto, el vector β~0 = (x0 , y 0 , z 0 ) tangente a la curva β será también tangente a la superficie S,
cuyo plano de vectores tangentes tiene por base los S~x = (1, 0, zx ), S~y = (0, 1, zy ), de modo que la
regla de la cadena nos dice que las derivadas (x0 , y 0 ) son las componentes del vector tangente β~0 a la
curva β respecto a la base de vectores tangentes a la superficie S que la contiene:
β~0 = (x0 , y 0 , z 0 ) = x0 (1, 0, zx ) + y 0 (0, 1, zy ) = x0 S~x + y 0 S~y .
10
f
α
• Caso D ⊆ R −
→ X ⊆ R3 −
→ Y ⊆ R. En este caso tenemos una función f : w = f (x, y, z) y una
curva paramétrica α contenida en su dominio. La regla de la cadena da
w0 =
∂w dx ∂w dy ∂w dz
dw
=
+
+
.
dt
∂x dt
∂y dt
∂z dt
Supongamos que f ◦ α = 0. Entonces la curva imagen de α está contenida en la superficie S
cuya ecuación implícita es f (x, y, z) = 0. Esto significa que, en cada punto, el vector gradiente de f ,
∇f = (wx , wy , wz ), es perpendicular a todos los vectores tangentes a las curvas contenidas en la
superficie y que pasan por el punto, que son los vectores del plano tangente a la superficie; se dice que
∇f es un vector normal a la superficie.
g
f
• Caso D ⊆ R2 −
→ X ⊆ R2 −
→ Y ⊆ R. En este caso suponemos que la función z = f (x, y) de dos
variables x, y se va a expresar como función de otras dos variables u, v a través de la función general
g que podemos expresar de la forma x = x(u, v), y = y(u, v). Si todas las funciones son derivables se
tiene
xu xv
zu = zx xu + zy yu ,
(zu , zv ) = (zx , zy )
= (zx xu + zy yu , zx xv + zy yv ),
yu yv
zv = zx xv + zy yv .
Lo podemos expresar con la notación de Leibniz:
∂w ∂x ∂w ∂y
∂w
=
·
+
·
,
∂u
∂x ∂u
∂y ∂u
3.3.
∂w
∂w ∂x ∂w ∂y
=
·
+
·
.
∂v
∂x ∂v
∂y ∂v
OPTIMIZACIÓN
Como en el caso de una variable, entenderemos por optimización encontrar los valores en los que
las funciones alcanzan valores máximos o mínimos, ya sean relativos o absolutos. Estudiaremos la
optimización para funciones de dos variables, pero los resultados se pueden generalizar para funciones
de n > 2 variables. Utilizaremos el término extremo para referirnos indistintamente a un máximo o
un mínimo.
Definición 9 (Extremos relativos). Sea f : U ⊂ R2 −→ R y (x0 , y0 ) ∈ U .
(i) f tiene un mínimo local o relativo en (x0 , y0 ) si existe B, una bola abierta centrada en
(x0 , y0 ) tal que f (x, y) ≥ f (x0 , y0 ) para todo (x, y) ∈ U ∩ B.
(ii) f tiene un máximo local o relativo en (x0 , y0 ) si existe B, una bola abierta centrada en
(x0 , y0 ) tal que f (x, y) ≤ f (x0 , y0 ) para todo (x, y) ∈ U ∩ B.
Definición 10 (Extremos absolutos). Sea f : U ⊂ R2 −→ R y (x0 , y0 ) ∈ U .
(i) f tiene un mínimo global o absoluto en (x0 , y0 ) si f (x, y) ≥ f (x0 , y0 ) para todo (x, y) ∈ U .
(ii) f tiene un máximo global o absoluto en (x0 , y0 ) si f (x, y) ≤ f (x0 , y0 ) para todo (x, y) ∈ U .
Ejemplos. Los ejemplos siguiente se justifican con sus gráficas, representadas a continuación de izquierda a derecha.
(i) f (x, y) = x2 + y 2 tiene un mínimo global (y por tanto local) en (0, 0).
(ii) g(x, y) = 1 − x2 − y 2 tiene un máximo global en (0, 0).
(iii) j(x, y) = x3 + y 3 − 2x2 − 4y 2 tiene en (0, 0) un máximo local, pero no global.
(iv) h(x, y) = x2 − y 2 no tiene extremos en el punto (0, 0).
1.0
0.5
0.0
-0.5
-1.0
-1
0
1
2
1.0
0.5
1.0
0.5
0.0
-0.5
0.0
-0.5
-1.0
2.0
0
1.0
-1.0
1.0
0.5
0.0
-0.5
0.5
-5
1.5
0.0
-1.0
1.0
0.5
0.0
1.0
-0.5
-0.5
-10
-1.0
0.5
-1.0
-1.0
-0.5
-0.5
0.0
0.0
-1.0
-0.5
0.0
0.0
0.5
1.0
-1.0
0.5
0.5
1.0
1.0
11
3.3.1.
Cálculo de extremos relativos en dominios abiertos
Suponemos funciones que tienen todas las derivada que se utilicen.
Definición 11 (Puntos críticos). Sea f : U ⊂ R2 −→ R y (x0 , y0 ) ∈ U un punto interior del
dominio. El punto (x0 , y0 ) es un punto crítico de f si en él se anula el gradiente de f , es decir, si
fx (x0 , y0 ) = 0 = fy (x0 , y0 ).
Teorema 2. Si (x0 , y0 ) es un extremo relativo de f entonces (x0 , y0 ) es un punto crítico de f .
Nota. El recíproco no es cierto: hay puntos críticos que no son extremos. Por ejemplo, el punto (0, 0)
es crítico de la función h del ejemplo (iv) anterior, pero no es máximo ni mínimo.
Definición 12 (Punto de silla). Llamaremos puntos de silla son los puntos críticos que no son
extremos relativos.
Ahora vamos a ver algunas condiciones suficientes para que un punto crítico sea extremo relativo.
Si f ∈ C 2 (U ), la relación entre puntos críticos y la matriz hessiana es:
(
fxx > 0 ⇒ mínimo estricto
det(Hf ) > 0 y
fxx < 0 ⇒ máximo estricto
det(Hf ) < 0 ⇒ punto silla
det(Hf ) = 0 ⇒ puede ser cualquier cosa
En este último caso hay que emplear otros métodos para poder decidir qué tipo de punto crítico
tenemos. Por ejemplo, si fxx > 0 o fyy > 0 podemos descartar que sea máximo y análogamente si
fxx < 0 o fyy < 0 podemos descartar que sea mínimo.
En general, para una función f (x1 , x2 , . . . , xn ) de n variables f : U ⊂ Rn −→ R, P = (p1 , . . . , pn ) ∈
U , se toman los menores principales de su matriz hessiana:
∆k (P ) =
fx1 x1 (P ) . . . fx1 xk (P )
...
...
...
,
fxk x1 (P ) . . . fxk xk (P )
k = 1, 2, . . . , n.
Entonces, si P es un punto crítico de f :
(i) Si ∆k (P ) > 0 para todo k = 1, . . . , n, entonces P es un mínimo relativo.
(ii) Si (−1)k ∆k (P ) > 0 para todo k = 1, . . . , n, entonces P es un máximo relativo.
3.3.2.
Extremos relativos condicionados
Estudiaremos máximos y mínimos locales de funciones cuyo dominio está restringido por alguna
condición dada por ecuaciones.
Ejemplo. Optimizar la función f (x, y) = x3 + y 3 − 3xy restringiendo sus variables a que estén en el
segmento l1 = {(x, −1) | 0 ≤ x ≤ 2}, es decir, a que sea y = −1, 0 ≤ x ≤ 2. En este caso se reduce el
problema a una variable: optimizar g(x) = f (x, 1) = x3 + 3x − 1 en el intervalo 0 ≤ x ≤ 2.
La formulación general del problema que trataremos es:
Optimizar z = f (x1 , x2 , . . . , xn )
g1 (x1 , x2 , . . . , xn ) = 0
sujeto a:
g2 (x1 , x2 , . . . , xn ) = 0
...
gm (x1 , x2 , . . . , xn ) = 0
m < n.
Si podemos despejar las variables en las igualdades de condición el problema se reducirá a otro de
menos variables, como en el ejemplo anterior. Pero hay un método que da bastante información en
casos más generales.
12
Método de los multiplicadores de Lagrange. Este método se basa en que un extremo condicionado de f con las restricciones gi = 0 es un punto crítico de la función de Lagrange
F (x1 , . . . , xn , λ1 , . . . , λm ) = f (x1 , . . . , xn ) + λ1 g1 (x1 , . . . , xn ) + · · · + λm g(x1 , . . . , xn ).
El método consiste en resolver el sistema de m + n ecuaciones con m + n incógnitas (las variables
xi y los multiplicadores de Lagrange λj ):
∂g1
∂g2
∂gm
∂f
∂F
=
0
∂x1
∂x1 + λ1 ∂x1 + λ2 ∂x1 + . . . + λm ∂x1 = 0
∂f
∂g
∂g
∂gm
∂F
1
2
∂x2 = 0
∂x2 + λ1 ∂x2 + λ2 ∂x2 + . . . + λm ∂x2 = 0
. . .
. . .
∂f
∂g1
∂g2
∂gm
∂F
es
decir,
=
0
∂xm
∂xn + λ1 ∂xn + λ2 ∂xn + . . . + λm ∂xn = 0
g1 (x1 , . . . , xn ) = 0
∂F = 0
∂λ1
.
.
.
...
g (x , . . . , x ) = 0.
∂F = 0
m 1
n
∂λm
y evaluar f en dichos puntos para determinar los que son extremos.
Nota. Las condiciones para poder aplicar este método son:
(i) f, g1 , . . . , gm tienen derivadas parciales de segundo orden continuas.
(ii) m < n, e.d. hay menos restricciones que variables.
1 ,...,gm )
(iii) El rango de la matriz jacobiana ∂(g
∂(x1 ,...,xn ) de las restricciones es m.
Nota. No estudiaremos en este curso las condiciones suficientes para poder afirmar que un punto
crítico de la función de Lagrange es máximo o mínimo.
3.3.3.
Extremos absolutos
D(a, r) = {x ∈ R2 | kx − ak ≤ r} disco cerrado.
Una región se dice cerrada si su complementario es un abierto (es decir, los bordes de dicha región
forman parte de la región).
Una región se dice acotada si está contenida dentro de un disco cerrado.
Teorema 3 (Weierstrass). Sea S ⊂ R2 un subconjunto cerrado y acotado y f una función continua
definida en S. Entonces f tiene máximo y mínimo absolutos en S.
Nota. El Teorema de Weierstrass da una condición suficiente para la existencia de extremos absolutos,
pero no necesaria. Es decir, el teorema asegura que una función continua con dominio cerrado y acotado
por fuerza tiene extremos absolutos, pero si la función no es continua, o el dominio no es cerrado o no
es acotado, puede que haya extremos absolutos o puede que no.
Para encontrar los extremos absolutos con dominios S cerrados y acotados:
1. Encontrar los puntos críticos de f que están en S (estarán en su interior).
2. Estudiar f en la frontera ∂S de S.
3. Comparar los valores de f en los puntos anteriores.
Nota. Estudiar la función en ∂S quiere decir hallar los extremos de f condicionados por las ecuaciones
implícitas de ∂S.
13