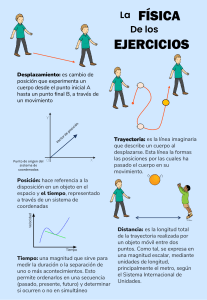
ESTRUCTURAS LAMINARES PARCIAL 2020 ALUMNO: PÉREZ L.U.N°: TEMA 1: Actividad 1: Para la placa cuadrada de Figura 1, aplicar el método de diferencias finitas (para la discretización de la misma, dividir en tres partes iguales cada lado) y calcular: a- Deformada – graficar (20 p) b- Momento flector en el punto P1 de coordendas (0,1/3 A) (5 p) c- Corte en P3 de coordenadas (A,1/3 A) d- (10 p) Momento torsor en P2 de coordenadas (1/3 A, 1/3 A) (5p) Figura 1 DATOS (en m, kN) – Defina el espesor A: 7 Material: H°A° q: 7 Actividad 2: la figura representa la sección transversal de una presa de gravedad, que se supone en estado plano (no considerar peso propio). Se propone entonces la siguiente función de Airy: ( x, y) A x y B x3 C x3 y D x y 3 E 5 x3 y 3 3 x y 5 Aplicar condición de biarmonicidad (5p) Derivar las tensiones (5p) Plantear condiciones de borde y determinar constantes (15 p) Determinar las tensiones principales en el punto de coordenadas (H/2, 0) (5p) Figura 2 Datos (m) H: 60 b= 6 Actividad 3: la aplicación de las cargas sobre el viaducto de la Figura 3 (que salva una luz de 7 metros), resulta en un momento torsor Mt que somete a la estructura a un estado de torsión uniforme. Determinar Estado tensional en las paredes (20 p) Rigidez torsional (5 p) Ángulo de torsión (5 p) DATOS (m - kN) A: 7 Espesores: B:5,5 e1: 0,15 Mt= 15800 kN m C: 5 e2: 0,25 D:7 e3: 0,10 Material: H°A° - definir tipo