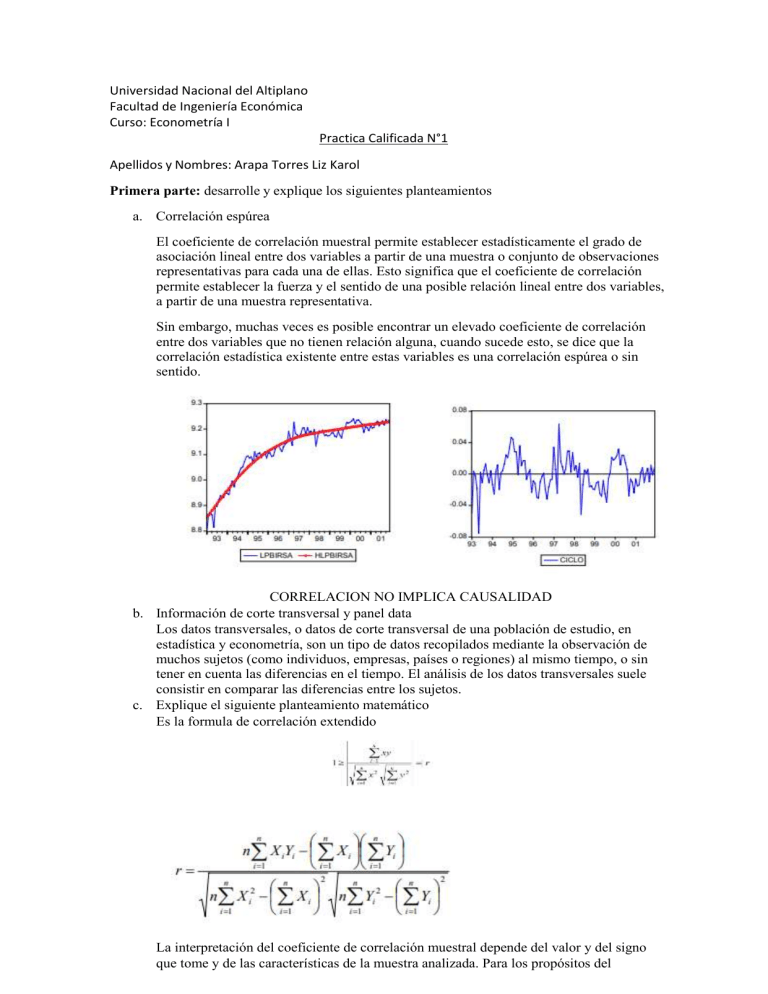
Universidad Nacional del Altiplano Facultad de Ingeniería Económica Curso: Econometría I Practica Calificada N°1 Apellidos y Nombres: Arapa Torres Liz Karol Primera parte: desarrolle y explique los siguientes planteamientos a. Correlación espúrea El coeficiente de correlación muestral permite establecer estadísticamente el grado de asociación lineal entre dos variables a partir de una muestra o conjunto de observaciones representativas para cada una de ellas. Esto significa que el coeficiente de correlación permite establecer la fuerza y el sentido de una posible relación lineal entre dos variables, a partir de una muestra representativa. Sin embargo, muchas veces es posible encontrar un elevado coeficiente de correlación entre dos variables que no tienen relación alguna, cuando sucede esto, se dice que la correlación estadística existente entre estas variables es una correlación espúrea o sin sentido. CORRELACION NO IMPLICA CAUSALIDAD b. Información de corte transversal y panel data Los datos transversales, o datos de corte transversal de una población de estudio, en estadística y econometría, son un tipo de datos recopilados mediante la observación de muchos sujetos (como individuos, empresas, países o regiones) al mismo tiempo, o sin tener en cuenta las diferencias en el tiempo. El análisis de los datos transversales suele consistir en comparar las diferencias entre los sujetos. c. Explique el siguiente planteamiento matemático Es la formula de correlación extendido La interpretación del coeficiente de correlación muestral depende del valor y del signo que tome y de las características de la muestra analizada. Para los propósitos del presente ensayo, se asume que el número de observaciones de la muestra (tamaño de muestra), es tal que la muestra es representativa: presenta las mismas características de la población. De esta manera, las conclusiones que puedan extraerse a partir del análisis del coeficiente de correlación serán válidas para la relación poblacional. 1< r < 1 Si lo demostramos Esta última expresión es una forma de escribir la desigualdad de Cauchy-Schwartz. A partir de esta expresión tenemos Por lo tanto se demuestra la afirmacion d. Explique la diferencia entre predicción y pronostico, utilice variables económicas para ilustrar un ejemplo. El pronóstico es el proceso de estimación en situaciones de incertidumbre. El término predicción es similar, pero más general, y usualmente se refiere a la estimación de series temporales o datos instantáneos. e. Explique regresores adecuados en el modelo de regresión clásico El modelo clásico de regresión lineal se basa en un conjunto de supuestos sobre la manera cómo se generan los datos a través de un proceso subyacente «generador de datos». La teoría normalmente especificará una relación determinista y precisa entre la variable dependiente y las variables independientes. Los supuestos del modelo hacen referencia a las siguientes cuestiones: 1. Forma funcional lineal de la relación, 2. Identificabilidad de los parámetros del modelo, 3. Valor esperado de la perturbación dada la información observada, 4. Varianzas y covarianzas de las perturbaciones dada la información observada, 5. Naturaleza de la muestra de los datos sobre las variables independientes, y 6. Distribución de probabilidad de la parte estocástica del modelo. Los supuestos describen la forma del modelo y las relaciones entre sus partes y disponen los procedimientos de estimación e inferencia adecuados. En esta sección se discutirá cada uno de los supuestos en detalle. f. En economía con modelos en los que el comportamiento de una variable, Y, se puede explicar a través de una variable X Explique, porque se desarrolla el siguiente proceso de optimización Este es el principio de minimos cuadrados Min (Yi ̂ 0 ̂ 1 X i ) 2 ̂ 0 , ̂ 1 Se eleva al cuadrado los errores para no tener que lidiar con errores negativos, con esto podemos minimizar baja las condiciones de primer orden Segunda parte: desarrolle los siguientes ejercicios 1. Dada una población de una cantidad importante de individuos, se tienen las siguientes variables aleatorias: Y = Número de veces que ha estado desempleado X = Cantidad de titulaciones Y se obtiene la siguiente frecuencia relativa (función de distribución conjunta): Y\X Y=1 Y=2 Y=3 Pr(x) Obtenga: a. b. c. d. e. E[Y] E[Y2] V[Y] E[YX] E[Y|x=1] X=1 0.4 0.2 0.05 0.65 X=2 0.2 0.1 0 0.3 X=3 0.05 0 0 0.05 Pr(y) 0.65 0.3 0.05 f. Argumente sobre la independencia de las variables a partir de E[Y|X]=E[Y] (recuerde es necesario probar esto para cada uno de los valores de X). 2. Dado el siguiente planteamiento del ejercicio; en la tabla siguiente se presenta las puntuaciones obtenidas en el examen de ingreso a la universidad en Estados Unidos, ACT (American College Test), y en el GPA (promedio escolar) de ocho estudiantes universitarios. El GPA esta medido en una escala de cuatro puntos y se ha redondeado a un digito después del punto decimal. Se pide lo siguiente: a. Realice el análisis: Presente su tabla de correlación Analice la presencia de correlación y correlación espúrea, explique Presente su grafico de dispersión b. Estime la relación entre GPA y ACT empleando MCO; es decir, obtenga las estimaciones para la pendiente y para el intercepto en la ecuación (utilice Excel). 𝐺𝑃𝐴𝑖 = 𝛽̂0 + 𝛽̂1 𝐴𝐶𝑇𝑖 + 𝑢𝑖 𝐴𝐶𝑇𝑖 = 𝛽̂0 + 𝛽̂1 𝐺𝑃𝐴𝑖 + 𝑢𝑖 c. Calcule los valores ajustados y los residuales para cada observación y verifique que los residuales (aproximadamente) sumen cero. Presente su tabla resumen para evidenciar sus resultados Presente sus resultados de forma matricial para un solo modelo (pregunta b) Parte 5: Debido a que el T-calculado es menor al T-tabla, se concluye que se puede afirmar que al 1% de significancia No existe una correlación lineal entre el X y Y.